【数据结构】二分搜索树详解-树数据结构

[[400829]]

一、树结构

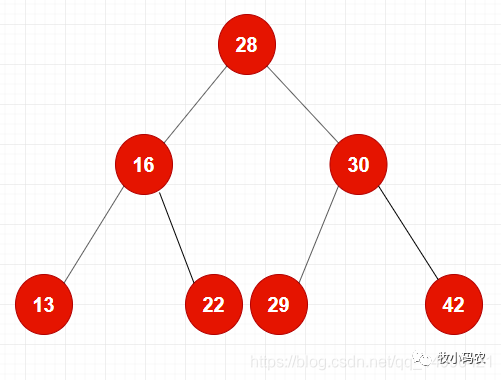
树是一种很特别的数据结构，树这种数据结构叫做 “树” 就是因为它长得像一棵树。但是这棵树画成的图长得却是一棵倒着的树，根在上，叶在下。树是图的一种，树和图的区别就在于：树是没有环的，而图是可以有环的。

树状图是一种数据结构，它是由n(n>=1)个有限节点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。

二、为什么要有树结构

2.1 树结构是一种天然的组织结构

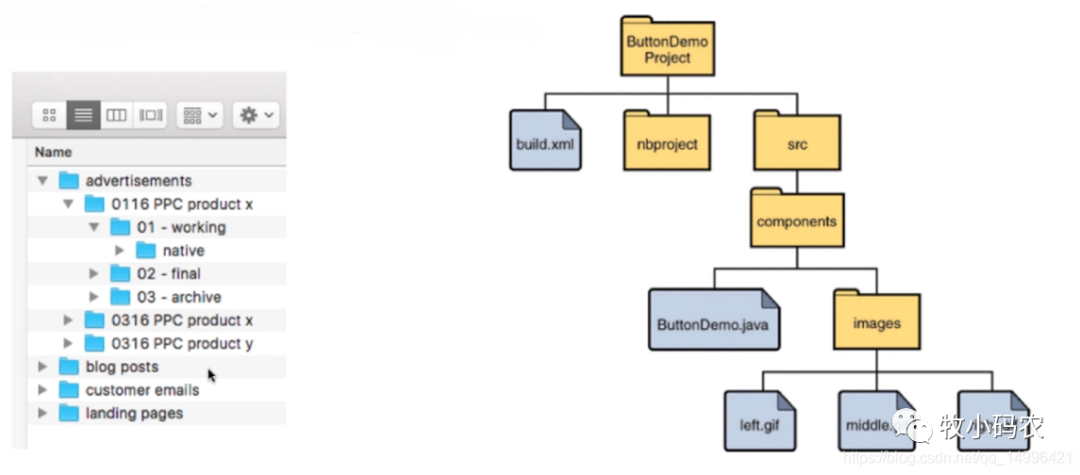
比如说电脑中的文件夹，我们需要找到一个特定的文件，需要到某个文件夹下去找这个文件，计算机的文件存储的结构来源于生活。再比如说图书馆，我们知道图书馆里面有历史类、数理类、计算机类，我们想要找到关于java的书籍，就需要到计算机类的Java中去找到我们需要的图书

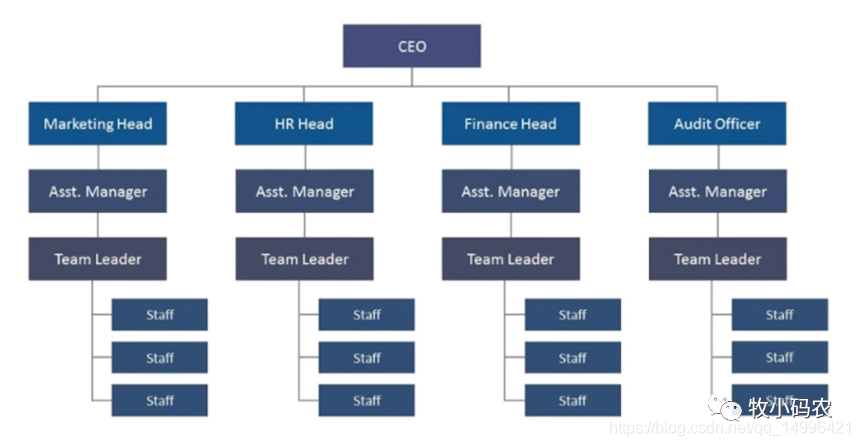
比如公司里面的层级结构：CEO、HR CTO等等，还有我们比较常见的家谱等等，都是类似于树结构

将数据使用树结构后，会更加的高效

三、二分搜索树

3.1 特点

二分搜索树是一个动态数据结构
二分搜索树也是一颗二叉树(也叫多叉树)
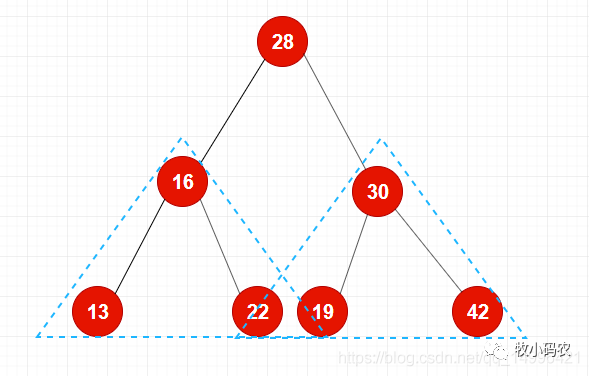
二分搜索树的每个节点的值都大于其左子树的所有节点的值，同时每个节点的值都小于其右子树的所有节点的值
存储的元素必须有可比较性, Java中的话就要求二分搜索树保存的数据类型要实现Comparable接口, 或者使用额外的比较器实现
每一颗子树也是二分搜索树
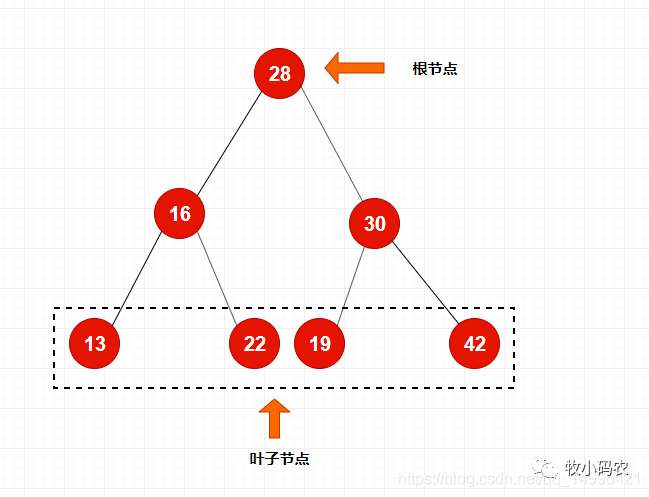
二分搜索树具有唯一根节点，同时在二叉树中最底下是它的叶子节点

二分搜索树具有唯根节点，每个节点最多有两个孩子(左边的叫左孩子，右边的叫右孩子)，同时每个节点最多有一个父亲

二分搜索树天然的具有递归特性

每个节点的左子树也是二叉树
每个节点的右子树也是二叉树

二叉树不一定是满的，一个接电脑也是二叉树、空也是二叉树

四、具体代码实现

在进行相关操作之前, 先定义一个支持泛型的节点类, 用于存储二分搜索树每个节点的信息, 这个类作为二分搜索树的一个内部类, 二分搜索树的类声明以及Node节点类声明如下:

public class BST> { 
 
private class Node{ 
 
public E e; 
 
public Node left,right; 
 
public Node(E e){ 
 
this.e = e; 
 
left = null; 
 
right = null; 
 
} 
 
} 
 
//节点 
 
private Node root; 
 
// 树容量 
 
private int size; 
 
public BST(){ 
 
root = null; 
 
size = 0; 
 
} 
 
public int size(){ 
 
return size; 
 
} 
 
public boolean isEmpty(){ 
 
return size == 0; 
 
} 
 
}

4.1 添加元素

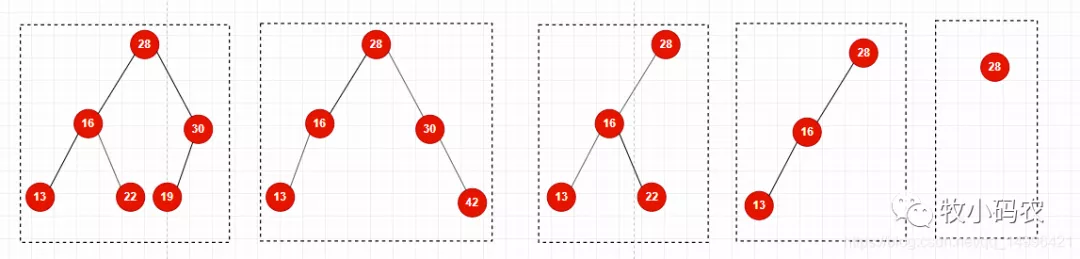
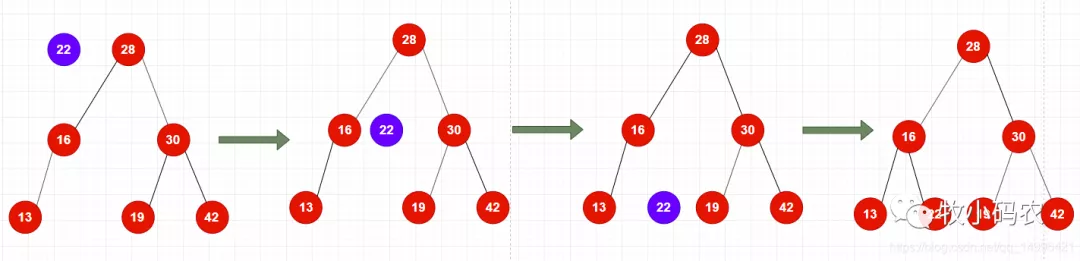
二分搜索树添加元素的非递归写法，和链表很像，由于二分搜索树本身的递归特性, 所以可以很方便的使用递归实现向二分搜索树中添加元素,

代码实现：

//向二分搜索树添加新的元素e 
 
public void add(E e){ 
 
root = add(root,e); 
 
} 
 
//向以Node为根的二分搜索树中插入元素 E，递归算法 
 
//返回插入新节点后二分搜索树的根 
 
private Node add(Node node,E e){ 
 
if(node == null){ 
 
size++; 
 
return new Node(e); 
 
} 
 
if(e.compareTo(node.e) < 0) 
 
node.left = add(node.left,e); 
 
else if(e.compareTo(node.e) > 0) 
 
node.right = add(node.right,e); 
 
return node; 
 
}

4.2 查找元素

由于二分搜索树没有下标, 所以针对二分搜索树的查找操作, 我们需要定义一个 contains() 方法, 查看二分搜索树是否包含某个元素, 返回一个布尔型变量

代码实现：

//看二分是搜索树中是否包含元素e 
 
public boolean contains(E e){ 
 
return contains(root,e); 
 
} 
 
//看以Node为根的二分搜索树中是否包含元素e，递归算法 
 
private boolean contains(Node node,E e){ 
 
if(node == null) 
 
return false; 
 
if(e.compareTo(node.e) == 0) 
 
return true; 
 
else if(e.compareTo(node.e) < 0) 
 
return contains(node.left,e); 
 
else //e.compareTo(node.e) > 0 
 
return contains(node.right,e); 
 
}

4.3 遍历操作

一、什么是遍历操作

遍历操作就是把所有的节点都访问一遍
访问的原因和业务相关
遍历分类

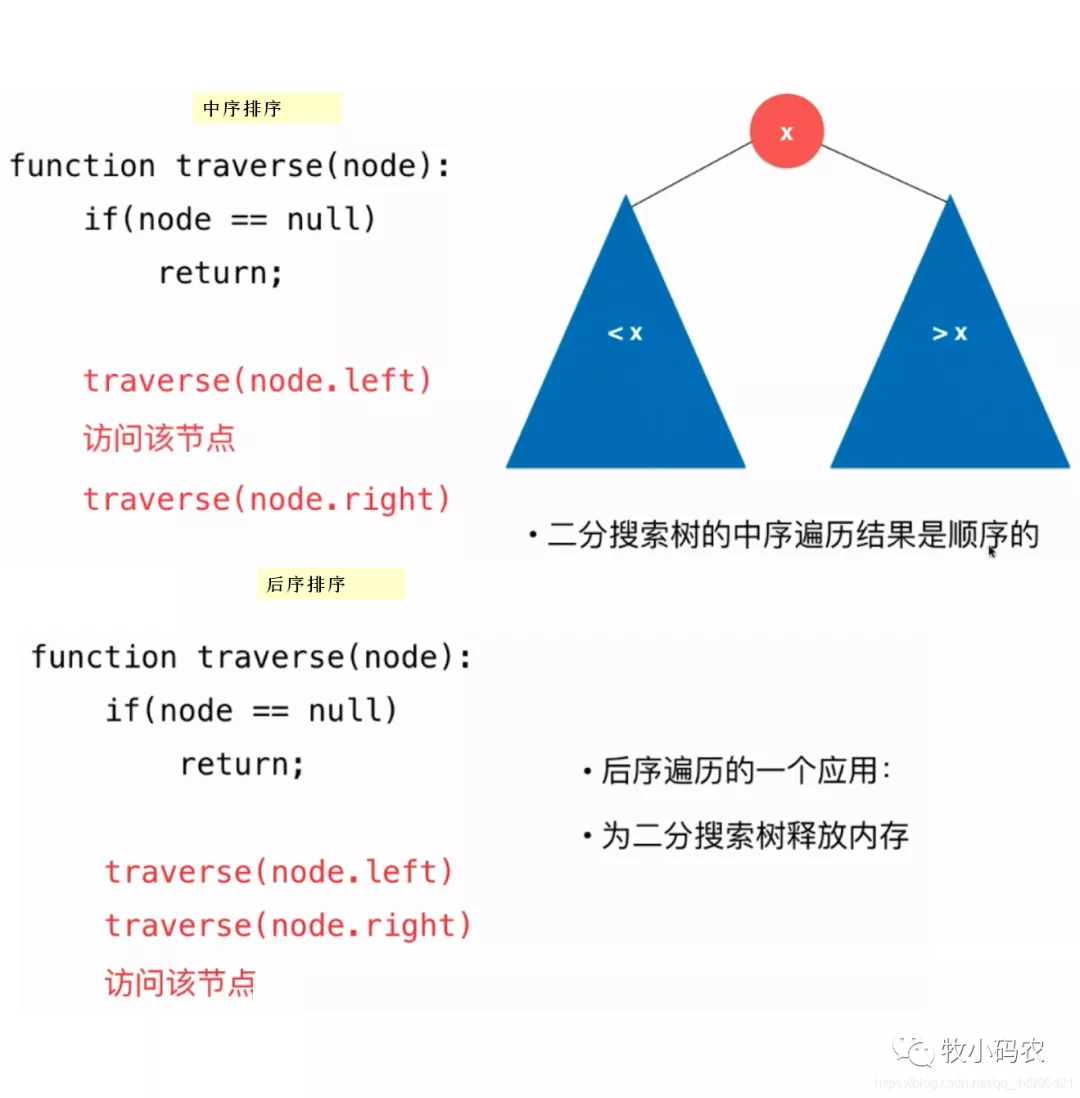
前序遍历 : 对当前节点的遍历在对左右孩子节点的遍历之前, 遍历顺序 : 当前节点->左孩子->右孩子中序遍历 : 对当前节点的遍历在对左右孩子节点的遍历中间, 遍历顺序 : 左孩子->当前节点->右孩子后序遍历 : 对当前节点的遍历在对左右孩子节点的遍历之后, 遍历顺序 : 左孩子->右孩子->当前节点

二、前序遍历

//二分搜索树前序遍历 
 
public void preOrder(){ 
 
preOrder(root); 
 
} 
 
//前序遍历以Node为根的二分搜索树，递归算法 
 
private void preOrder(Node node){ 
 
if(node == null) 
 
return; 
 
System.out.println(node.e); 
 
preOrder(node.left); 
 
preOrder(node.right); 
 
} 
 
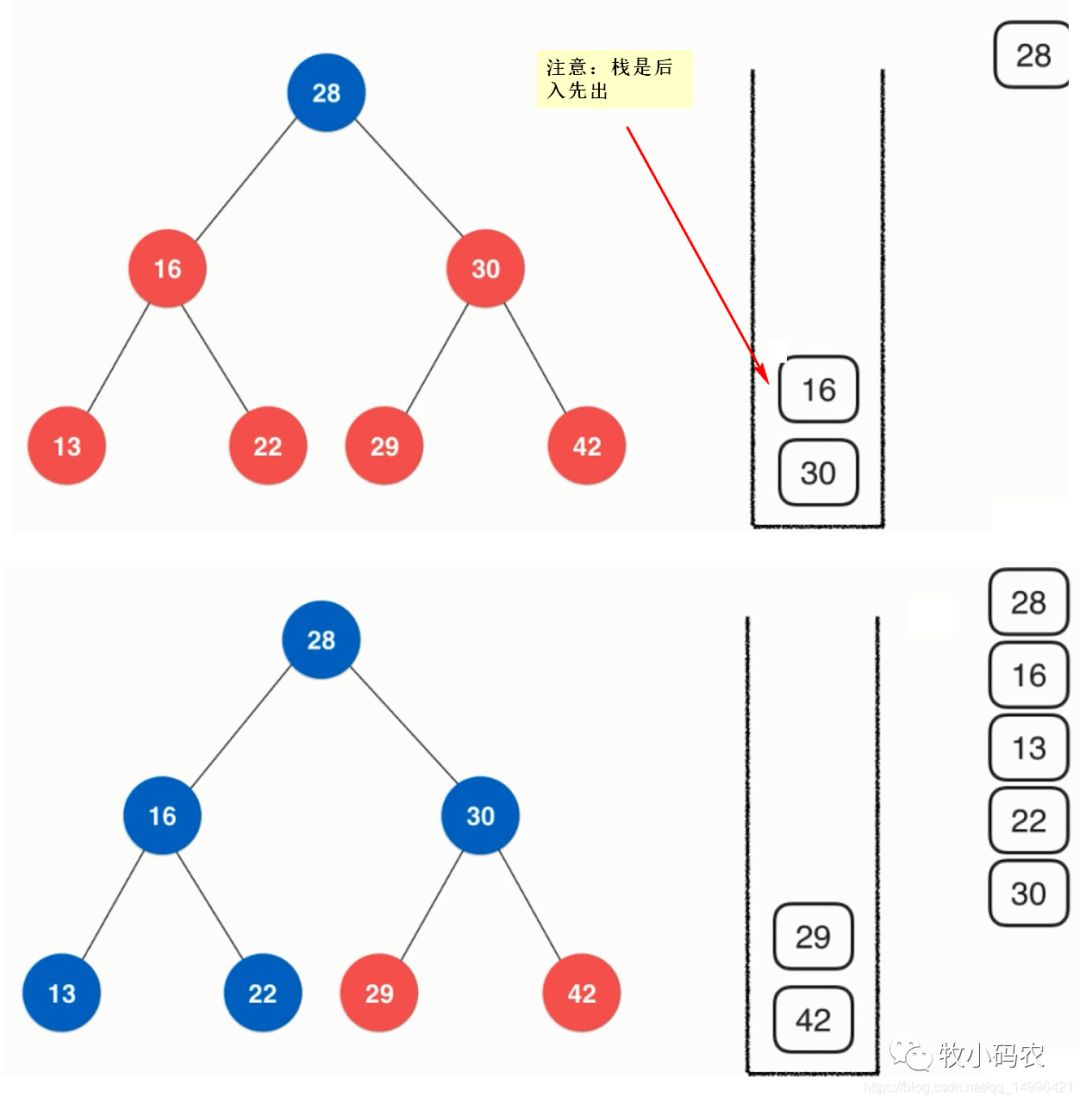
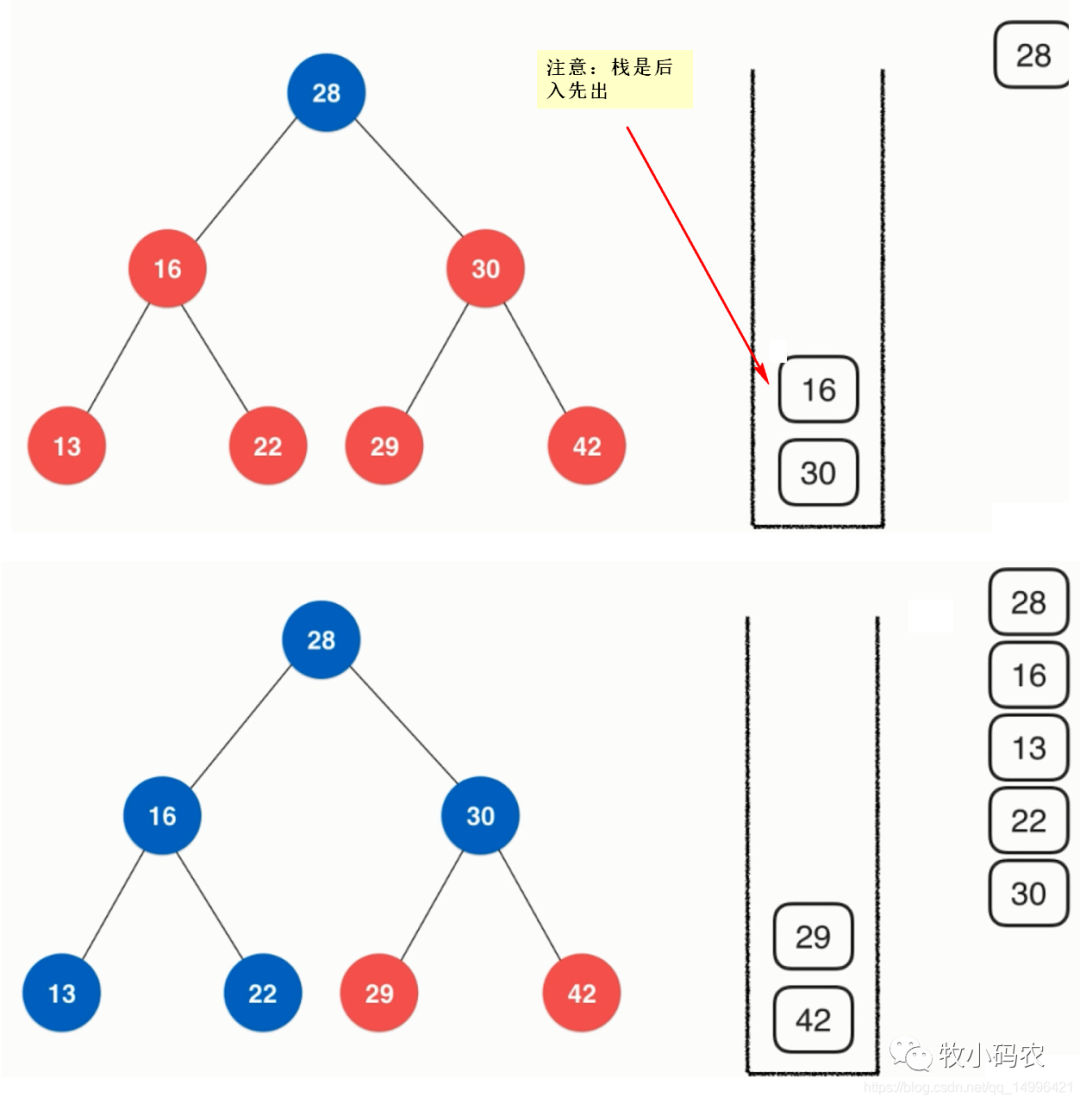
public void preOrderNR(){ 
 
Stack stack = new Stack<>(); 
 
stack.push(root); 
 
while(!stack.isEmpty()){ 
 
Node cur = stack.pop(); 
 
System.out.println(cur.e); 
 
if(cur.right != null) 
 
stack.push(cur.right); 
 
if(cur.left != null) 
 
stack.push(cur.left); 
 
} 
 
}

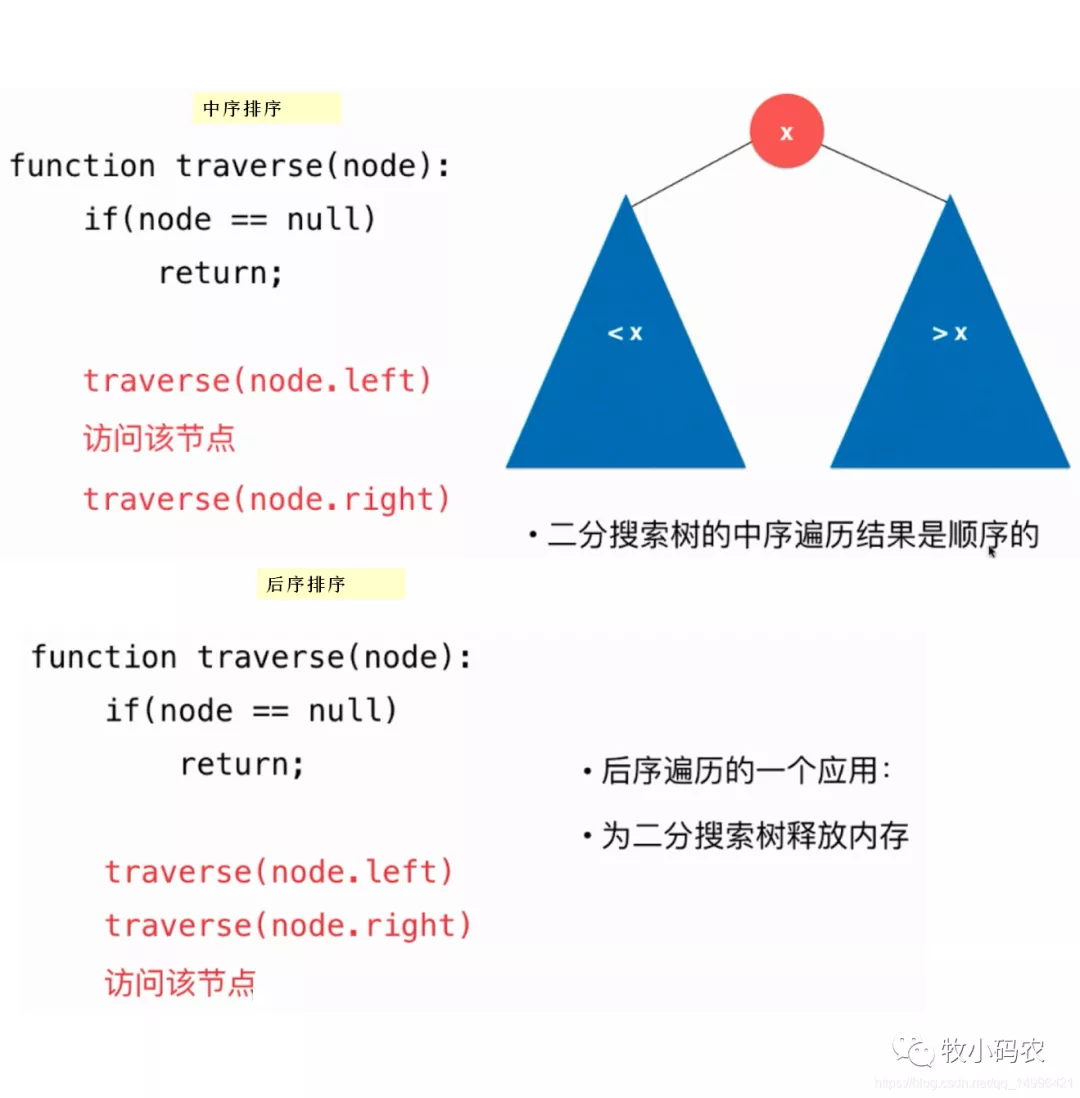
三、中序遍历

//二分搜索树的中序遍历 
 
public void inOrder(){ 
 
inOrder(root); 
 
} 
 
//中序遍历以Node为根的二分搜索树，递归算法 
 
private void inOrder(Node node){ 
 
if(node ==null) 
 
return; 
 
inOrder(node.left); 
 
System.out.println(node.e); 
 
inOrder(node.right); 
 
}

四、后序遍历

//二分搜索树的后序遍历 
 
public void postOrder(){ 
 
inOrder(root); 
 
} 
 
public void levelOrder(){ 
 
Queue q = new LinkedList(); 
 
q.add(root); 
 
while (!q.isEmpty()){ 
 
Node cur = q.remove(); 
 
System.out.println(cur.e); 
 
if(cur.left != null) 
 
q.add(cur.left); 
 
if(cur.right != null) 
 
q.add(cur.right); 
 
} 
 
} 
 
//后序遍历以Node为根的二分搜索树，递归算法 
 
private void postOrder(Node node){ 
 
if(node ==null) 
 
return; 
 
inOrder(node.left); 
 
inOrder(node.right); 
 
System.out.println(node.e); 
 
}

五、理解前中后

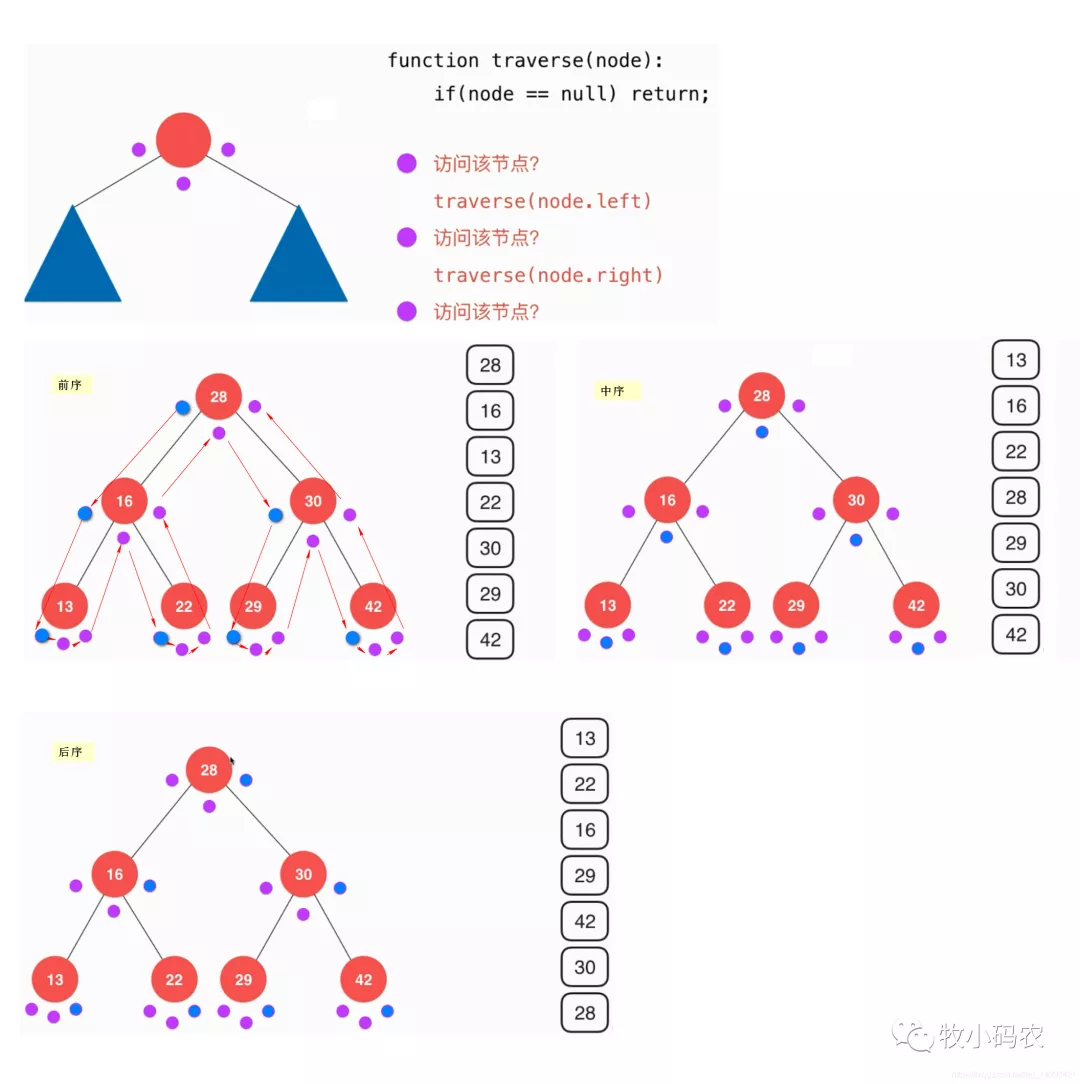
二分搜索树前序非递归写法

【数据结构】二分搜索树详解