一、前言
在前面两章我们讲解了动态数组、栈和队列的讲解,这些底层都是依托静态数组,靠 resize解决固定容量问题的,之前虽然用户看到的是动态数组,但是依然使用的是静态数组,他是依靠 resize 这个方法解决 固定容量问题 ,但是我们今天要讲解的 链表 不一样,链表是我们数据结构学习的一个重点,也有可能是一个难点,为什么链表这么重要呢?因为他是最简单的也是 真正的动态数据结构。
二、为什么链表很重要
- 链表是一个真正的动态数据结构
- 最简单的动态数据结构
- 更深入的理解引用(或者指针)
- 更深入的理解递归
- 辅助组成其他数据结构
更深入的理解引用(或者指针):和内存相关,虽然在 java 中大家不用手动的管理内存,但是对 链表 这种数据结构,更加深入的理解,可以帮助大家对引用、指针、甚至计算机系统中和内存管理相关的很多话题,有更加深入的认识。
更深入的理解递归:链表 本来也是有他非常清晰的递归结构的,、由于 链表 这种数据结构是 数据结构,我们可以更加 深入理解递归,对于递归这种深入理解是不可获取的。
链表 本身也是具有功能性:辅助组成其他数据结构(hashMap 、栈和队列)
三、什么是链表
链表 是一种数据结构,在内存中通过 节点记录内存地址 而相互链接形成一条链的储存方式。相比数组而言,链表在内存中不需要连续的区域,只需要每一个节点都能够 记录下一个节点 的 内存地址 ,通过 引用 进行查找,这样的特点也就造就了 链表 增删操作时间消耗很小,而查找遍历时间消耗很大的特点。
我们日常在 Java 中使用的 LinkedList 即为 双向链表。而在链表是由其基本组成单元节点 (Node) 来实现的。我们在日常中见到的链表大部分都是 单链表和双链表
单元节点 (Node):
- class Node{
- E e;
- Node next;
- }
e 就是链表元素
next 指的是当前节点的下一个节点
对于 链表 来说它就像我们的火车一样,每一个节点其实就是一节车厢,我们在车厢中存储真正的数据,而车厢和车厢之间还要进行连接,让我们数据是整合在一起的,用户可以方便的在所有的数据上进行查询或其他操作,那么 数据和数据连接 就是由这个 next 来完成的
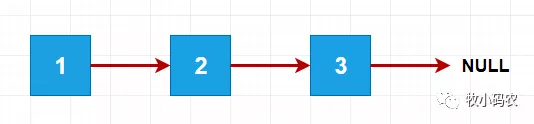
当然 链表 不能无穷无尽,如果一个节点的 next 是 Null 了,就说明这个节点是最后一个节点了,这就是 链表
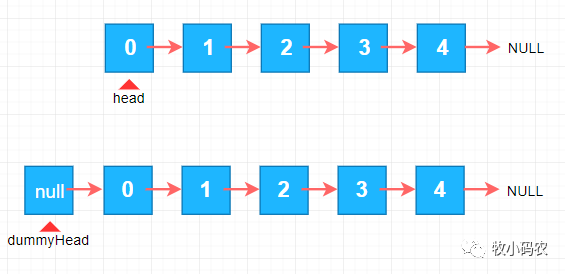
如下图所示(单链表):
链表的优点:真正的动态,不需要处理固定容量的问题链表的缺点:丧失了随机访问的能力
在数组中:每一个索引,直接从数组中拿出索引对应的元素,这是因为从底层机制上,数组所开辟的空间,在内存里是连续分布的,所以我们可以直接可以去找这个数组的偏移,直接计算出这个数据所存储的内存地址,可以直接使用。
链表:而链表是靠 Next 一层一层连接的,需要借助这个 Next 一点一点的去找我们需要取出来的元素。
四、创建我们自己的链表
4.1 链表基本结构
- /**
- * 底层链表的内部类
- * @param <E>
- */
- public class LinkedList<E> {
- //设计私有的内部类,对于用户来说不需要知道链表底层实现,
- // 不需要知道node这个节点,对用户屏蔽编码实现的底层实现
- private class Node{
- public E e;
- public Node next;//public 可以在LinkedList随意操作
- public Node(E e,Node next){
- this.e = e;
- this.next = next;
- }
- public Node(E e){
- this(e,null);
- }
- public Node(){
- this(null,null);
- }
- @Override
- public String toString() {
- return e.toString();
- }
- }
- }
内部类Node:设计私有的内部类,对于用户来说不需要知道链表底层实现,不需要知道node这个节点,对用户屏蔽编码实现的底层实现e:元素next:指向Node的一个引用
4.2 添加元素
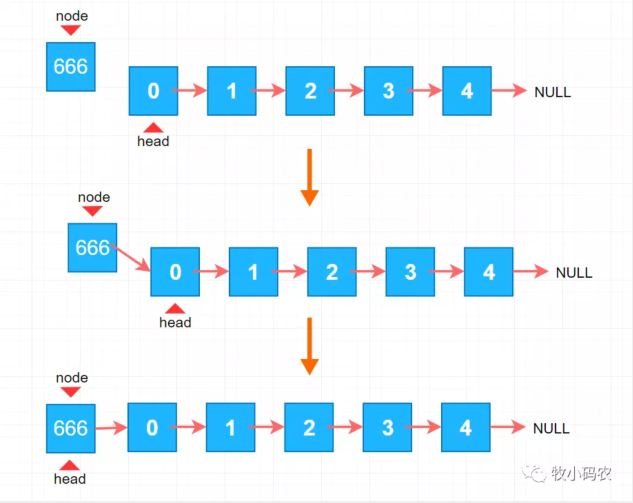
之前我们讲的是如何在数组中添加元素,我们在数组尾添加元素是非常方便的,因为对于数组来说是顺序排放的,有意思的是对于链表来说,恰恰相反,在链表头添加元素是非常方便的,其实这样非常好理解,对于数组来说我们有 size 这个变量,它直接指向了数组中最后一个元素下一个位置,也就是下一个待添加元素的位置,所以直接添加就非常容易,因为有 size 这个变量,在跟踪数组的尾巴,而对于链表来说我们设立了链表的一个头 head ,而没有变量来跟踪链表的尾巴,所以我们在链表头添加元素是非常方便的,最关键的就是 node.next = head 和 head = node,如下图所示:
4.2.1 链表头添加元素
代码实现:
- //在链表头中添加元素e
- public void addFirst(E e){
- //方式一
- // Node node = new Node(e);
- // node.next = head;
- // head = node;
- //方式二
- head = new Node(e,head);
- size ++;
- }
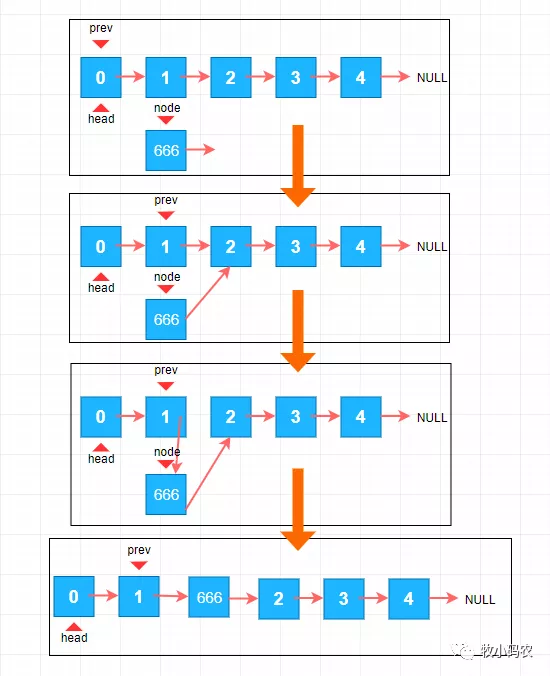
4.2.2 链表中间添加元素
我们需要在索引为2的地方添加元素 666,我们只需要找到 元素666要 插入之前的节点(1) ,我们管它叫 prev,然后把 之前节点的(1) next 指向 666,然后在将 666的这个 节点指向之前节点(1) 的 之后的节点(2) ,就完成了整个插入了,其中关键代码就是 node.next=prev.next和prev.next=node;,其中关键:我们要找到添加节点的前一个节点 。
代码实现:
- //在链表的index(0-based)位置添加新的元素e
- public void add(int index,E e){
- if(index < 0 || index > size)
- throw new IllegalArgumentException("Add failed. Illegal index.");
- if(index == 0)
- addFirst(e);
- else{
- Node prev = head;
- for (int i = 0; i < index - 1; i++) {//将prev 放入下一个节点,直到移动到index - 1
- prev = prev.next;
- //方式一
- // Node node = new Node(e);
- // node.next = prev.next;
- // prev.next = node;
- //方式二
- prev.next = new Node(e,prev.next);
- size++;
- }
- }
- }
- //在链表末尾添加新的元素e
- public void addLast(E e){
- add(size,e);
- }
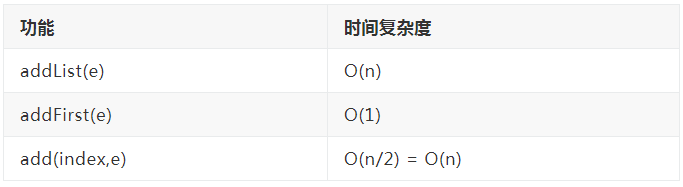
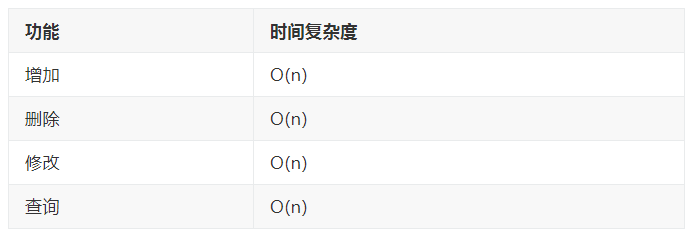
4.2.3 添加操作时间复杂度
4.3 为链表设计虚拟头结点
上面我们介绍了链表的添加操作,那么我们在添加的时候遇到了一个问题,就是在链表任意一个地方的时候,添加一个元素,在链表头添加一个元素,和在链表其他地方添加元素,逻辑上会有差别,为什么在链表头添加元素会比较特殊呢,因为我们在链表添加元素的过程,要找到待添加的 之前的一个节点,但是由于对于链表头没有之前的一个节点,不过我们可以自己创建一个头结点,这个头节点就是 虚拟头结点,这个节点对于用户来说是不存在, 用户也不会感知到这个节点的存在,我们是屏蔽了这个节点的存在,如下图所示:
代码实现:
- private Node dummyHead;
- int size;
- public LinkedList(){
- dummyHead = new Node(null,null);
- size = 0;
- }
- //获取链表中的元素个数
- public int getSize(){
- return size;
- }
- //返回链表是否为空
- public boolean isEmpty(){
- return size == 0;
- }
- //在链表的index(0-based)位置添加新的元素e
- public void add(int index,E e){
- if(index < 0 || index > size)
- throw new IllegalArgumentException("Add failed. Illegal index.");
- Node prev = dummyHead;
- for (int i = 0; i < index; i++)
- prev = prev.next;
- prev.next = new Node(e,prev.next);
- size ++;
- }
- //在链表头中添加元素e
- public void addFirst(E e){
- add(0,e);
- }
- //在链表末尾添加新的元素e
- public void addLast(E e){
- add(size,e);
- }
4.4 链表元素 get、set、是否存在操作
- //在链表的index(0-based)位置添加新的元素e
- public E get(int index){
- if(index < 0 || index > size)
- throw new IllegalArgumentException("Get failed. Illegal index.");
- Node cur = dummyHead.next;
- for (int i = 0; i < index; i++)
- cur = cur.next;
- return cur.e;
- }
- //获得链表的第一个元素
- public E getFirst(){
- return get(0);
- }
- //获取链表的最后一个元素
- public E getLast(){
- return get(size - 1);
- }
- //在链表的index(0-based)位置添加新的元素e
- public void set(int index,E e){
- if(index < 0 || index > size)
- throw new IllegalArgumentException("Set failed. Illegal index.");
- Node cur = dummyHead.next;
- for (int i = 0; i < index; i++)
- cur = cur.next;
- cur.e = e;
- }
- //查找链表中是否有元素e
- public boolean contains(E e){
- Node cur = dummyHead.next;
- while (cur != null){
- if(cur.e.equals(e))
- return true;
- cur = cur.next;
- }
- return false;
- }
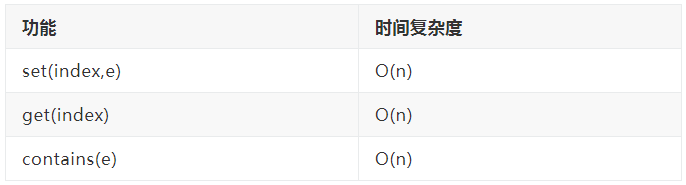
4.5.1 修改和查找操作时间复杂度
4.5 删除链表元素
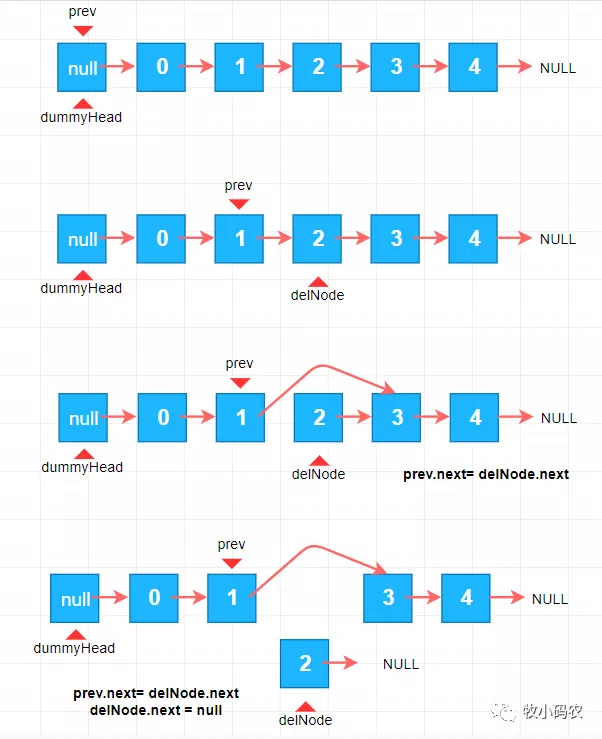
加入我们想要删除索引为 (2) 位置的元素,我们需要找到 待删除节点之前的一个位置,也就是(1) ,我们用 prev 表示,找到这个节点之后,那么 (2) 就是我们需要删除的索引了 我们叫 delNode,如下图所示:
代码实现:
- //从链表中删除Index(0-based)位置的元素,返回删除的元素
- public E remove(int index){
- if(index < 0 || index > size)
- throw new IllegalArgumentException("Remove failed. Illegal index.");
- Node prev = dummyHead;
- for (int i = 0; i < index; i++)
- prev = prev.next;
- Node retNode = prev.next;
- prev.next = retNode.next;
- retNode.next = null;
- size --;
- return retNode.e;
- }
- //从链表中删除第一个位置的元素
- public E removeFirst(){
- return remove(0);
- }
- //从链表中删除最后一个位置的元素
- public E removeLast(){
- return remove(size - 1);
- }
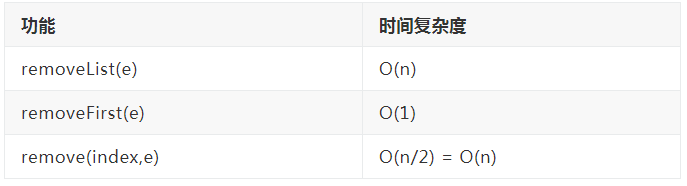
4.5.1 删除操作时间复杂度
4.6 完整代码
- /**
- * 底层链表的内部类
- * @param <E>
- */
- public class LinkedList<E> {
- private class Node{
- public E e;
- public Node next;//public 可以在LinkedList随意操作
- public Node(E e,Node next){
- this.e = e;
- this.next = next;
- }
- public Node(E e){
- this(e,null);
- }
- public Node(){
- this(null,null);
- }
- @Override
- public String toString() {
- return e.toString();
- }
- }
- private Node dummyHead;
- int size;
- public LinkedList(){
- dummyHead = new Node(null,null);
- size = 0;
- }
- //获取链表中的元素个数
- public int getSize(){
- return size;
- }
- //返回链表是否为空
- public boolean isEmpty(){
- return size == 0;
- }
- //在链表头中添加元素e
- public void addFirst(E e){
- //方式一
- // Node node = new Node(e);
- // node.next = head;
- // head = node;
- //方式二
- add(0,e);
- }
- //在链表的index(0-based)位置添加新的元素e
- public void add(int index,E e){
- if(index < 0 || index > size)
- throw new IllegalArgumentException("Add failed. Illegal index.");
- Node prev = dummyHead;
- for (int i = 0; i < index; i++)
- prev = prev.next;
- prev.next = new Node(e,prev.next);
- size ++;
- }
- //在链表末尾添加新的元素e
- public void addLast(E e){
- add(size,e);
- }
- //在链表的index(0-based)位置添加新的元素e
- public E get(int index){
- if(index < 0 || index > size)
- throw new IllegalArgumentException("Get failed. Illegal index.");
- Node cur = dummyHead.next;
- for (int i = 0; i < index; i++)
- cur = cur.next;
- return cur.e;
- }
- //获得链表的第一个元素
- public E getFirst(){
- return get(0);
- }
- //获取链表的最后一个元素
- public E getLast(){
- return get(size - 1);
- }
- //在链表的index(0-based)位置添加新的元素e
- public void set(int index,E e){
- if(index < 0 || index > size)
- throw new IllegalArgumentException("Set failed. Illegal index.");
- Node cur = dummyHead.next;
- for (int i = 0; i < index; i++)
- cur = cur.next;
- cur.e = e;
- }
- //查找链表中是否有元素e
- public boolean contains(E e){
- Node cur = dummyHead.next;
- while (cur != null){
- if(cur.e.equals(e))
- return true;
- cur = cur.next;
- }
- return false;
- }
- //从链表中删除Index(0-based)位置的元素,返回删除的元素
- public E remove(int index){
- if(index < 0 || index > size)
- throw new IllegalArgumentException("Remove failed. Illegal index.");
- Node prev = dummyHead;
- for (int i = 0; i < index; i++)
- prev = prev.next;
- Node retNode = prev.next;
- prev.next = retNode.next;
- retNode.next = null;
- size --;
- return retNode.e;
- }
- //从链表中删除第一个位置的元素
- public E removeFirst(){
- return remove(0);
- }
- //从链表中删除最后一个位置的元素
- public E removeLast(){
- return remove(size - 1);
- }
- @Override
- public String toString() {
- StringBuilder res = new StringBuilder();
- for (Node cur = dummyHead.next;cur != null; cur= cur.next)
- res.append(cur + "->");
- res.append("Null");
- return res.toString();
- }
- }
4.2.7 结果测试:
- public static void main(String[] args) {
- LinkedList<Integer> linkedList = new LinkedList<>();
- //添加元素 0-4
- for (int i = 0; i < 5 ; i++) {
- linkedList.addFirst(i);
- System.out.println(linkedList);
- }
- //添加第二个元素添加 666
- linkedList.add(2,666);
- System.out.println(linkedList);
- //删除第二个元素 666
- linkedList.remove(2);
- System.out.println(linkedList);
- //删除第一个元素
- linkedList.removeFirst();
- System.out.println(linkedList);
- //删除最后一个元素
- linkedList.removeLast();
- System.out.println(linkedList);
- }
打印结果:
- 0->Null
- 1->0->Null
- 2->1->0->Null
- 3->2->1->0->Null
- 4->3->2->1->0->Null
- 4->3->666->2->1->0->Null
- 4->3->2->1->0->Null
- 3->2->1->0->Null
- 3->2->1->Null
四、链表时间复杂度分析
对于增加和删除来说,如果是对链表头进行操作,那么就是 O(1) 级别的复杂度,对于查询来说,也是一样
五、链表应用
5.1 使用栈实现链表
5.1.1 接口类:
- /**
- * @program: Data-Structures
- * @ClassName Stack
- * @description:
- * @author: lyy
- * @create: 2019-11-20 21:51
- * @Version 1.0
- **/
- public interface Stack<E> {
- int getSize();
- boolean isEmpty();
- void push(E e);
- E pop();
- E peek();
- }
5.1.2 实现类:
- import com.lyy.datasty.Mystack.Stack;
- //链表栈实现
- public class LinkedListStack<E> implements Stack<E> {
- private LinkedList1<E> list;
- public LinkedListStack(){
- list = new LinkedList1<>();
- }
- @Override
- public int getSize() {
- return list.getSize();
- }
- @Override
- public boolean isEmpty() {
- return list.isEmpty();
- }
- @Override
- public void push(E e) {
- list.addFirst(e);
- }
- @Override
- public E pop() {
- return list.removeFirst();
- }
- @Override
- public E peek() {
- return list.getFirst();
- }
- @Override
- public String toString() {
- StringBuilder res = new StringBuilder();
- res.append("Stack:top ");
- res.append(list);
- return res.toString();
- }
- }
5.1.3 运行结果:
- public static void main(String[] args) {
- LinkedListStack<Integer> stack = new LinkedListStack<>();
- for (int i = 0; i < 5; i++) {
- stack.push(i);
- System.out.println(stack);
- }
- stack.pop();
- System.out.println(stack);
- }
5.1.4 结果打印:
- Stack:top 0->Null
- Stack:top 1->0->Null
- Stack:top 2->1->0->Null
- Stack:top 3->2->1->0->Null
- Stack:top 4->3->2->1->0->Null
- Stack:top 3->2->1->0->Null
5.2 使用链表实现队列
5.2.1 接口类
- /**
- * @program: Data-Structures
- * @ClassName Queue
- * @description:
- * @author: lyy
- * @create: 2019-11-21 21:54
- * @Version 1.0
- **/
- public interface Queue<E> {
- int getSize();
- boolean isEmpty();
- void enqueue(E e);
- E dequeue();
- E getFront();
- }
5.2.2 实现类
- public class LinkedListQueue<E> implements Queue<E>{
- //设计私有的内部类,对于用户来说不需要知道链表底层实现,
- // 不需要知道node这个节点,对用户屏蔽编码实现的底层实现
- private class Node{
- public E e;
- public Node next;//public 可以在LinkedList随意操作
- public Node(E e, Node next){
- this.e = e;
- this.next = next;
- }
- public Node(E e){
- this(e,null);
- }
- public Node(){
- this(null,null);
- }
- @Override
- public String toString() {
- return e.toString();
- }
- }
- private Node head,tail;
- private int size;
- public LinkedListQueue(){
- head = null;
- tail = null;
- size = 0;
- }
- @Override
- public int getSize() {
- return size;
- }
- @Override
- public boolean isEmpty() {
- return size == 0;
- }
- @Override
- public void enqueue(E e) {
- if(tail == null){
- tail = new Node(e);
- head = tail;
- }else{
- tail.next = new Node(e);
- tail = tail.next;
- }
- size ++;
- }
- @Override
- public E dequeue() {
- if(isEmpty())
- throw new IllegalArgumentException("Cannot dequeue from an empty queue.");
- Node retNode = head;
- head = head.next;
- retNode.next = null;
- if(head == null)
- tail = null;
- size --;
- return retNode.e;
- }
- @Override
- public E getFront() {
- if(isEmpty())
- throw new IllegalArgumentException("queue is empty.");
- return head.e;
- }
- @Override
- public String toString() {
- StringBuilder res = new StringBuilder();
- res.append("Queue:front ");
- Node cur = head;
- while (cur != null) {
- res.append(cur + "->");
- cur = cur.next;
- }
- res.append("Null tail");
- return res.toString();
- }
- }
5.2.2 测试类
- public static void main(String[] args) {
- LinkedListQueue<Integer> queue = new LinkedListQueue<>();
- for (int i = 0; i < 10; i++) {
- queue.enqueue(i);
- System.out.println(queue);
- if(i % 3 ==2){
- queue.dequeue();
- System.out.println(queue);
- }
- }
- }
打印结果:
- Queue:front 0->Null tail
- Queue:front 0->1->Null tail
- Queue:front 0->1->2->Null tail
- Queue:front 1->2->Null tail
- Queue:front 1->2->3->Null tail
- Queue:front 1->2->3->4->Null tail
- Queue:front 1->2->3->4->5->Null tail
- Queue:front 2->3->4->5->Null tail
- Queue:front 2->3->4->5->6->Null tail
- Queue:front 2->3->4->5->6->7->Null tail
- Queue:front 2->3->4->5->6->7->8->Null tail
- Queue:front 3->4->5->6->7->8->Null tail
- Queue:front 3->4->5->6->7->8->9->Null tail
六、更多链表结构
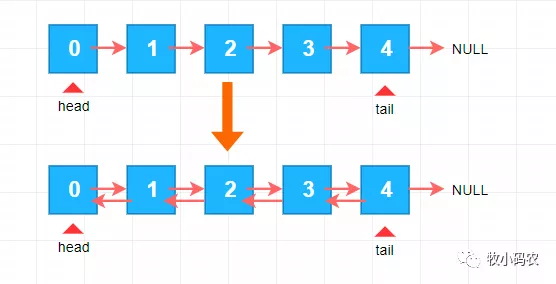
6.1 双链表
代码:
- class Node{
- E e;
- Node next,prev;
- }
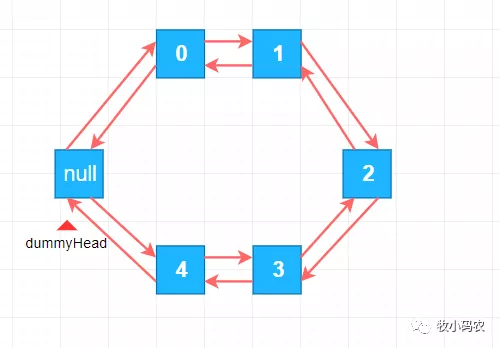
6.1 循环列表
代码:
- class Node{
- E e;
- Node next,prev;
- }
在java中,LinkedList 底层使用的就是 循环链表,也就是循环双向链表,到这里我们链表就讲解完成了。