算法介绍
- 分治法是一种很重要的算法。字面上的解释是“分而治之”,就是把一个复杂的问题分成两个或更多相同或相似的子问题,再把子问题分成更小的子问题…直到最后子问题可以简单的直接求解,原问题解即是子问题的解的合并。这个技巧是很多高效算法的基础,如排序算法(快速排序、归并排序),傅里叶变换(快速傅里叶变换)...
- 分支算法可以求解的一些经典文图:二分搜索、大整数乘法、棋盘覆盖、合并排序、快速排序、线性时间选择、最接近点对问题、循环赛日程表、汉诺塔。
分治算法的基本步骤
分治法在每一层递归上都有三个步骤:
- 分解:将原有问题分解为若干个规模较小,相互独立,与原问题形式相同的子问题
- 解决:若干子问题规模较小而容易被解决则直接解决,否则递归地解决各个子问题
- 合并:将各个子问题的解合并为原问题的解
分治算法设计模式
分治(Divide-and-Conquer(P))算法模式如下图,
其中|P| 表示问题P的规模,n0为一阀值,表示当问题p的规模不超过n0时,问题已容易直接解出,不必再继续分解。ADHOC(P)是该分治算法中的基本子算法,用于直接解小规模的问题P。因此,当P的规模不超过n0时直接用ADHOC(P)求解。算法MERGE(y1,y2,…yk)是该分治法中的合并子算法,用于将P的子问题P1,P2,…Pk的相应解y1,y2…yk合并为P的解。
分治算法实践-汉诺塔
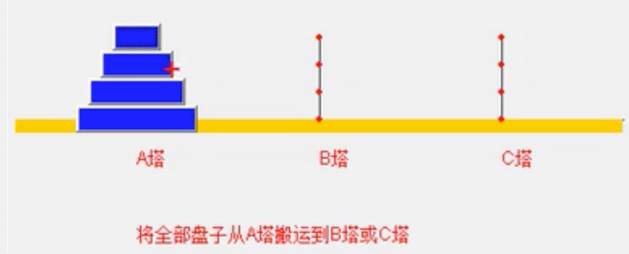
在一根柱子上从下往上按照大小顺序放着64片黄金圆盘,把圆盘从下面开始按大小顺序重新摆放在另一根柱子上,并且规定,在小圆盘上不能放大圆盘,在三根柱子之间一次只能移动一个盘。
思路分析:
- 如果是有一个盘,A->C
- 如果是 n>=2 盘情况,我们总是可以看成两个盘,一个是最下边的一个盘,一个是上面的所有盘:先把最上面的所有盘从A移动到B,把最下面的一个盘从A移动到C,把B塔的所有盘从B移动到C。
- package com.xie.algorithm;
- public class Hanoitower {
- public static void main(String[] args) {
- hanoiTower(3, 'A', 'B', 'C');
- /**
- * 第1个盘从A->C
- * 第2个盘从A->B
- * 第1个盘从C->B
- * 第3个盘从A->C
- * 第1个盘从B->A
- * 第2个盘从B->C
- * 第1个盘从A->C
- */
- }
- public static void hanoiTower(int num, char a, char b, char c) {
- //如果只有一个盘
- if (num == 1) {
- System.out.println("第1个盘从" + a + "->" + c);
- } else {
- //如果是 n>=2 盘情况,我们总是可以看成两个盘,一个是最下边的一个盘,一个是上面的所有盘
- //1.先把最上面的盘从A移动到B,移动过程会使用到C
- hanoiTower(num - 1, a, c, b);
- //2.把最下面的一个盘从A移动到C
- System.out.println("第" + num + "个盘从" + a + "->" + c);
- //3.把B塔的所有盘从B移动到C,移动过程使用到A塔
- hanoiTower(num - 1, b, a, c);
- }
- }
- }
【编辑推荐】