本文转载自微信公众号「景禹」,作者景禹。转载本文请联系景禹公众号。
页面替换算法
功能:当缺页中断发生,需要调入新的页面而内存已满时,选择内存当中哪个物理页面被置换。
目标:尽可能地减少页面的换进换出次数(即缺页中断的次数)。具体来说,把未来不再使用的或短期内较少使用的页面换出,通常只能在局部原理指导下依据过去的统计数据来进行预测。
最优页面替换算法
基本思路:当一个缺页中断发生时,对于保存在内存当中的每一个逻辑页面,计算在它的下一次访问之前,还需等待多长时间,从中选择等待时间最长的那个作为被置换的页面。
这只是一种理想情况,在实际中无法实现,因为操作系统无法知道每一个页面要等待多长时间以后才会被再次访问。
可用作其它算法的性能评价的依据(在一个模拟器上运行某个程序,并记录每一次的页面访问情况,在第二遍运行时即可使用最优算法)。
简单一句话,最优页面替换算法就是替换在将来最长时间内不需要的页面。
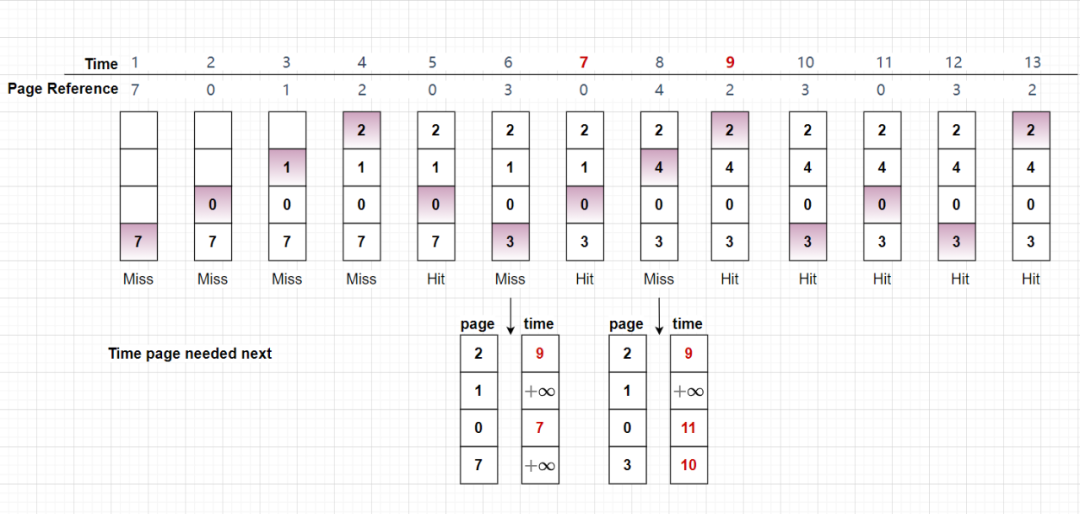
假设页帧(Page Frames)的大小为 4, 请求页面序列为:7, 0, 1, 2, 0, 3, 0, 4, 2, 3, 0, 3, 2,采用最优页面替换算法的缺页异常(Page Fault)的次数为多少?
初始时,页槽均为空,所以请求页面 7 0 1 2 被分配到空的页槽,产生 4 次缺页异常。
紧接着,请求页面 0 时,发现已经存在页帧中,0 次缺页异常;
当请求页面 3 时,页面 7 由于为在将来最长时间内不需要访问,所以被 3 替换,1 次缺页异常。
0 号页面命中,0 次页面异常;
请求页面 4 不存在页帧中,替换页面 1 ,1 次缺页异常;
对之后的请求页面序列 2,3,0,3,2 而言,均命中,固无缺页异常。
所以总共发生了 6 次缺页异常,即图中的 Miss 状态,其中的 Hit 表示命中,无缺页异常产生。
模拟实现一个最优页面替换算法:
输入 : 页帧数 fn = 3
页面 pg[] = {7, 0, 1, 2, 0, 3, 0, 4, 2, 3, 0, 3, 2, 1, 2, 0, 1, 7, 0, 1};
输出 : 命中次数 hits = 11 缺页异常 miss = 9
输入 : 页帧数 fn = 4 页面 pg[] = {7, 0, 1, 2, 0, 3, 0, 4, 2, 3, 0, 3, 2};
输出 : 命中次数 hits = 7 缺页异常 miss = 6
我们以页帧数 4 ,请求序列 {7, 0, 1, 2, 0, 3, 0, 4, 2, 3, 0, 3, 2} 为例进行说明。
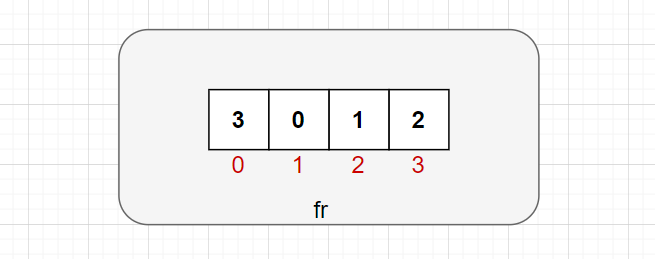
首先我们创建一个空的数组 fr 模拟页帧:
请求页面 7,发现不在数组 fr 当中且数组 fr 的大小 fr.size() < fn 页帧大小,则直接将请求页面 7 插入数组 fr中:
请求页面 {0,1,2} 与请求页面 7 情况类似,则依次将其添加到数组当中:
紧接着请求页面 0,遍历数组 fr ,发现 0 号页面已经在其中了,则命中次数 hit 加 1。
请求 3 号页面,遍历数组 fr ,发现不在其中且数组已满(fr.size == fn ),则需要找到要替换的页面,此时选择替换在将来最长时间内不需要的页面 。这里的将来最长时间不需要的页面,我们可以使用页面数组 pg[] 的下标进行表示。
遍历数组 fr[] ,并结合请求页面数组 pg[] 找到在将来最长时间内不需要的页面。
fr[0] = 7 ,我们从 3 号页面开始在数组 pg[] 中向后查找 7 号页面,发现其根本不存在,也就说 7 号页面就是在将来最长时间内不需要的页面。所以 3 号页面替换 7 号页面。
再访问 0 号页面,发现存在,则跳过;
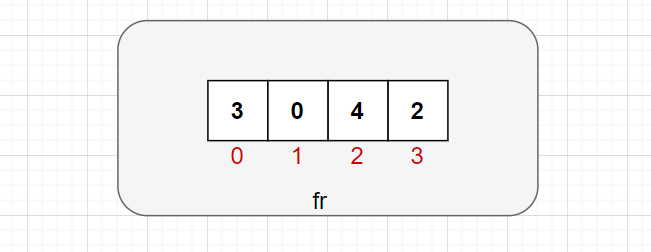
访问 4 号页面,发现不在页帧数组 fr 当中,则替换掉在将来最长时间内不需要的页面 1:
之后访问页面 {2, 3, 0, 3, 2} 均为命中,总共命中 6 次。
参考实现
#include <bits/stdc++.h>
using namespace std;
// 用于检查页帧中是否存在当前要访问的页 key
bool search(int key, vector<int>& fr)
{
for (int i = 0; i < fr.size(); i++)
if (fr[i] == key)
return true;
return false;
}
// 用于预测将来
int predict(int pg[], vector<int>& fr, int pn, int index)
{
// 存储在将来最近要使用的页面的索引
int res = -1, farthest = index;
for (int i = 0; i < fr.size(); i++) {
int j;
for (j = index; j < pn; j++) {
if (fr[i] == pg[j]) {
if (j > farthest) {
farthest = j;
res = i;
}
break;
}
}
// 如果某个页面将来从未被引用过,请将其返回。
if (j == pn)
return i;
}
// 如果 fr 中的所有页在将来都没出现过,则返回其中任何页,我们返回 0。否则我们将返回 res。
return (res == -1) ? 0 : res;
}
/**
* pg[] 请求页面序列
* pn 请求页面数
* fn 页帧数
*/
。
void optimalPage(int pg[], int pn, int fn)
{
// 为给定数量的帧创建一个数组,并将其初始化为空。
vector<int> fr;
// 遍历页面引用数组并检查未命中和命中。
int hit = 0;
for (int i = 0; i < pn; i++) {
// 在内存中命中页面 : HIT
if (search(pg[i], fr)) {
hit++;
continue;
}
// 页面在内存中不存在 : MISS
// 如果页帧中有可用的空间,则直接将缺失页加入其中。
if (fr.size() < fn) {
fr.push_back(pg[i]);
}
else { // 找到要替换的页
int j = predict(pg, fr, pn, i + 1);
fr[j] = pg[i];
}
}
cout << "命中次数 = " << hit << endl;
cout << "未命中次数 = " << pn - hit << endl;
}
int main()
{
int pg[] = { 7, 0, 1, 2, 0, 3, 0, 4, 2, 3, 0, 3, 2 };
int pn = sizeof(pg) / sizeof(pg[0]);
int fn = 4;
optimalPage(pg, pn, fn);
return 0;
}
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
- 25.
- 26.
- 27.
- 28.
- 29.
- 30.
- 31.
- 32.
- 33.
- 34.
- 35.
- 36.
- 37.
- 38.
- 39.
- 40.
- 41.
- 42.
- 43.
- 44.
- 45.
- 46.
- 47.
- 48.
- 49.
- 50.
- 51.
- 52.
- 53.
- 54.
- 55.
- 56.
- 57.
- 58.
- 59.
- 60.
- 61.
- 62.
- 63.
- 64.
- 65.
- 66.
- 67.
- 68.
- 69.
- 70.
- 71.
- 72.
- 73.
- 74.
- 75.
- 76.
- 77.
- 78.
其中的 search 函数大家可以换成哈希或者二分查找等,其中最关键的是 predict() 函数,用于查找在将来最长时间内不会使用到的页面,其实也就是两层 for 循环嵌套。
先进先出算法
FIFO(First In,First Out)就是先进先出算法。
基本思路:选择在内存中驻留时间最长的页面并淘汰。具体来说,系统维护着一个链表,记录了所有位于内存当中的逻辑页面。从链表的排列顺序来看,链首页面的驻留时间最长,链尾页面的驻留时间最短。当发生一个缺页中断时,把链首页面淘汰出局,并把新的页面添加到链表的末尾。
性能较差,调出的页面可能是经常要访问的页面,并且产生 Belady 现象,FIFO 算法很少单独使用。
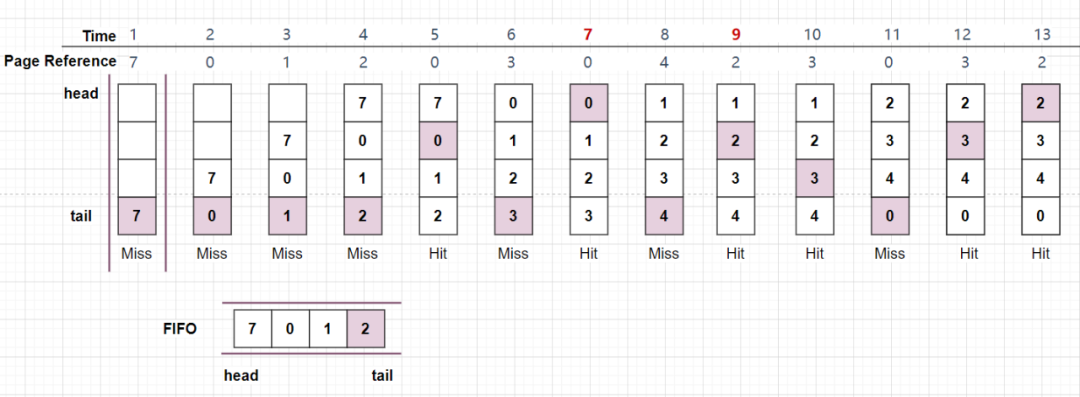
假设页帧(Page Frames)的大小为 4, 请求页面序列为:7, 0, 1, 2, 0, 3, 0, 4, 2, 3, 0, 3, 2,采用 FIFO 算法的缺页异常的次数为多少?
如上图所示,FIFO,先进先出,类似队列的特性。
对于请求页面 7,0,1,2 ,发生 4 次缺页中断,分别为其分配页;
访问页面 0 时,命中;
访问页面 3 时,缺页异常,此时会淘汰掉位于队列头的页面 7 ,将页面 3 插入到队尾,即选择在内存中驻留时间最长的页面并淘汰。
页面 0 命中;
访问页面 4 时,发生缺页异常,此时淘汰页面 0 ;
访问页面 2 和 3 时,均命中;
访问页面 0 时,缺页异常,淘汰页面 1 ,插入页面 0 ;
最后访问页面 3 和 2 均命中。
共发生缺页异常次数为 7 次。
最近最少使用算法
关于最近最少页面替换是算法的详细信息可以参考:最近最少使用 LRU 算法
时钟页面置换算法
Clock 页面置换算法,LRU 的近似,对 FIFO 的一种改进;
基本思路:
- 需要用到页表顶当中的访问位(Access Bit),当一个页面被装入内存时,把该位初始化为 0。然后如果这个页面被访问(读写),则把该位置置为 1。
- 把各个页面组织成环形链表(类似钟表面),把指针指向最老的页面(最先进来的页面);
- 当发生一个缺页中断时,考察指针所指向的最老页面,若它的访问位为 0 ,立即淘汰;若访问位为 1,则把该位置置为 0,然后指针向下移动一格。如此下去,直到找到被淘汰的页面,然后把指针移动到它的下一格。
假设页帧(Page Frames)的大小为 4, 请求页面序列为:7, 0, 1, 2, 0, 3, 0, 4, 2, 3, 0, 3, 2,采用 时钟页面替换算法的缺页异常的次数为多少?
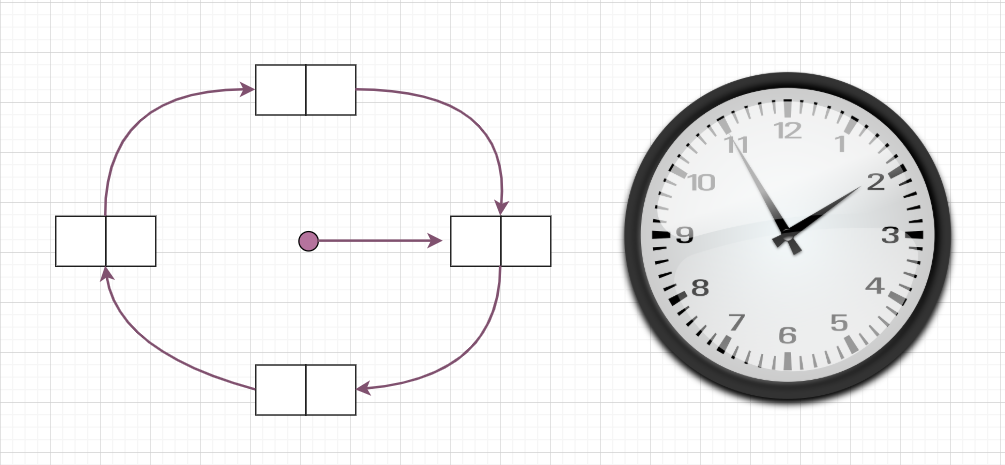
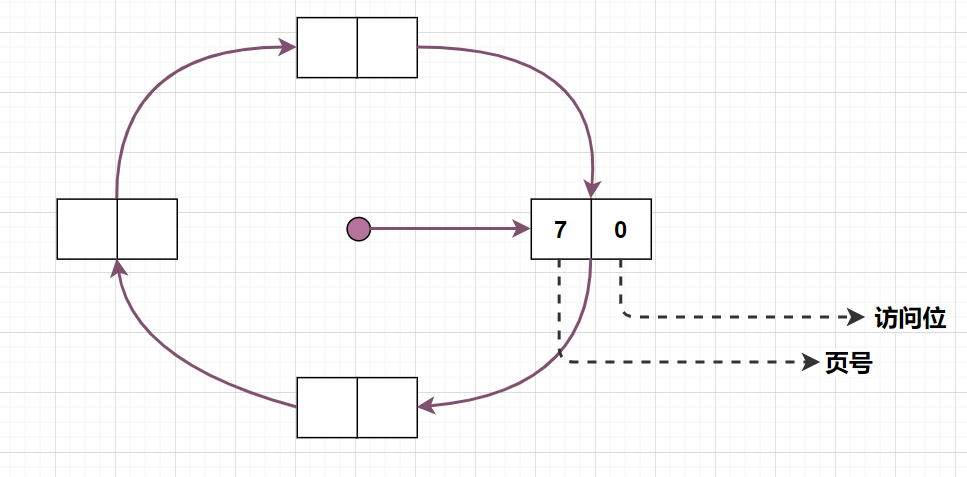
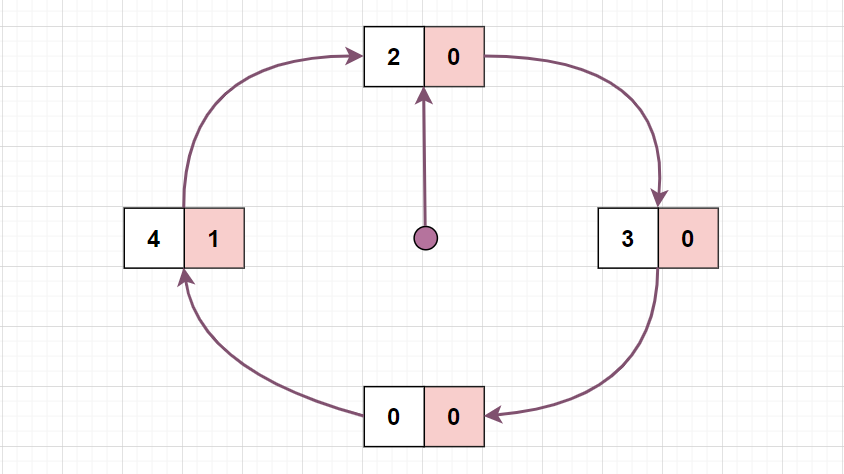
初始时,页帧为空,如下图所示的一个环形链表,是不是很想一个时钟:
请求页面 7,产生缺页中断,则将其装入内存,把该页面的访问位初始化为 0:
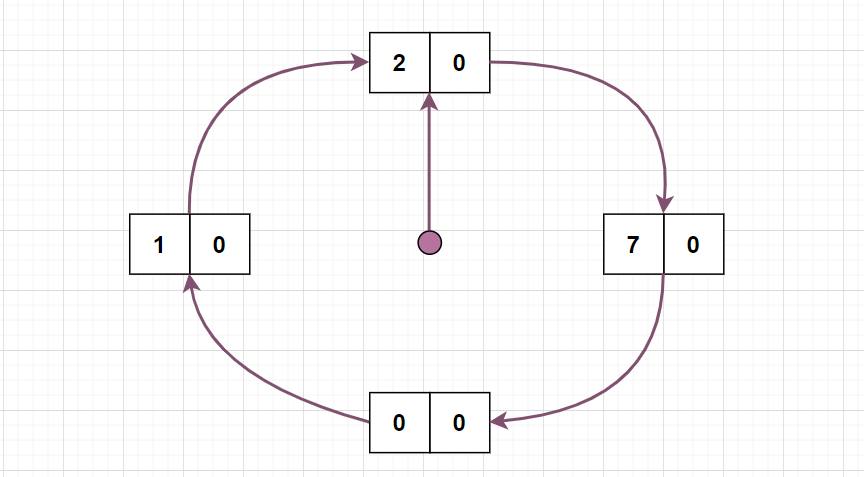
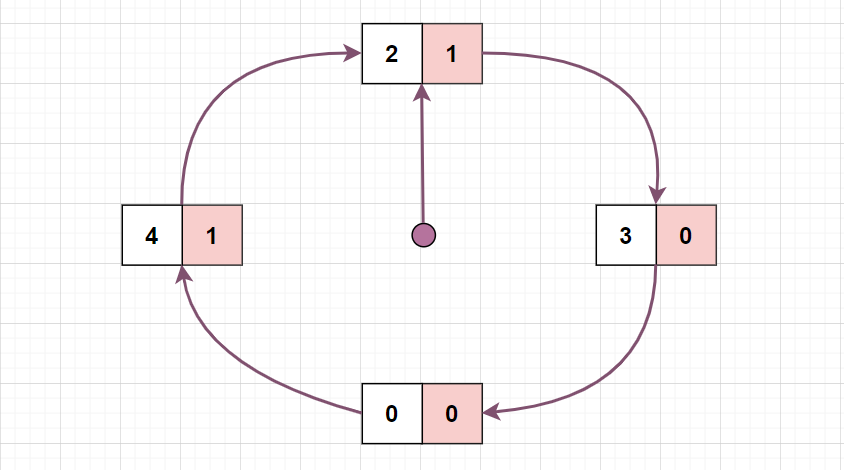
依次访问页面 0、1 和 2,与前面的方法类似:
紧接着请求页面 0 ,发现页面 0 已经在内存中了,则硬件会把访问位置为 1,并将指针下移:
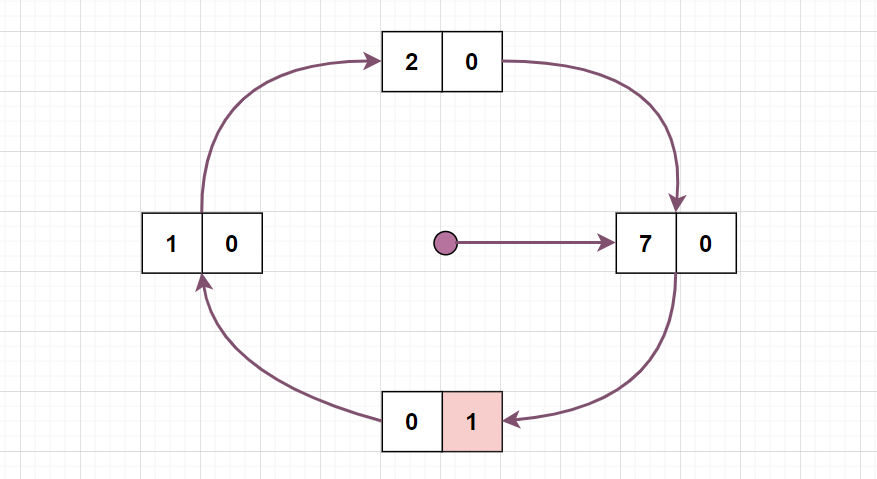
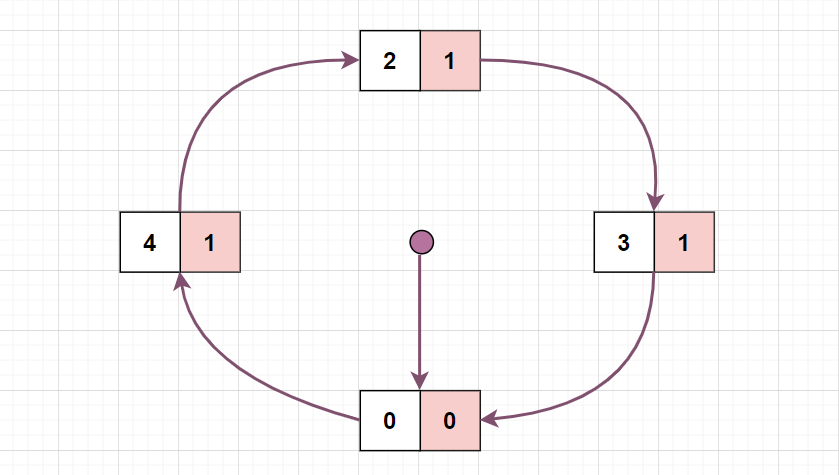
请求页面 3 时,发生缺页中断,此时指针所指向的页面 7 的访问位为 0,则立即淘汰掉并替换为页面 3,访问位为 1:
请求页面 0,已存在内存中,硬件将其访问位置为 1,与上图一样,没有变化;
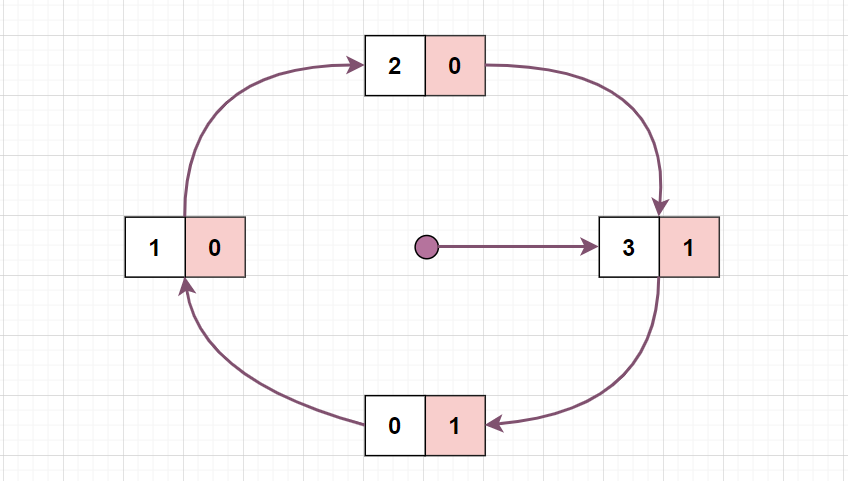
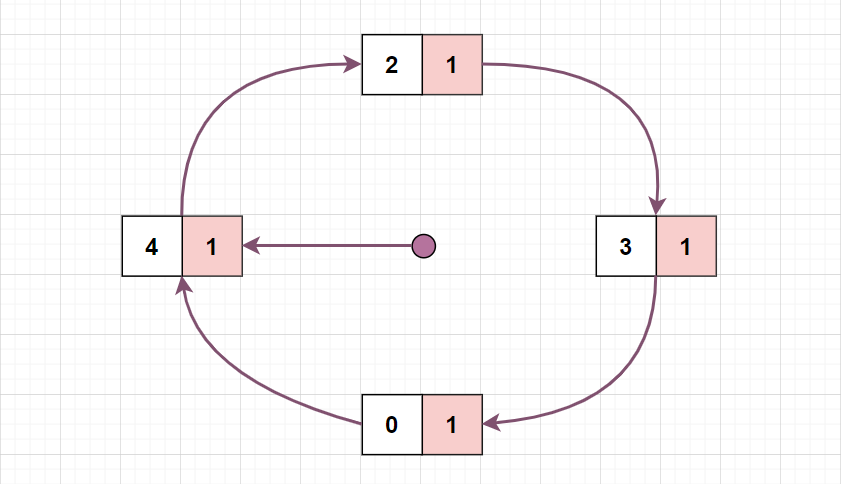
请求页面 4,发生缺页中断,首先将 3号页面的访问位置为 0, 0 号页面的访问位置为 0,指针下移,发现 1 号页面的访问位为0,则淘汰页面 1,替换为 4,访问位置 1 并下移指针:
请求页面 2 ,已存在内存中,硬件将其访问位置 1:
请求 3 号页面,将 3 号页面的访问位置为 1,将指针下移:
请求 0 号页面,将 0 号页面的访问位置 1,指针下移:
总的缺页中断次数为 5 次。
最不常用算法 LFU
基本思路:当一个缺页中断发生时,选择访问次数最少的那个页面,并淘汰之。
实现方法:对每一个页设置一个访问计数器,每当一个页面被访问时,该页面的访问计数器加 1。在发生缺页中断时,淘汰计数值最小的那个页面。如果所有页具有相同的频率,则对该页采取 LRU 方法并删除该页。
LRU 和 LFU 的区别:LRU 考察的是多久未访问,时间越短越好;而 LFU 考虑的是访问次数或频度,访问次数越多越好。
本文转载自微信公众号「景禹」,可以通过以下二维码关注。转载本文请联系景禹公众号。