本文经AI新媒体量子位(公众号ID:QbitAI)授权转载,转载请联系出处。
强化学习(RL)算法持续“进化”中……
来自Google Research的研究人员,证明可以使用图表示 (graph representation)和AutoML的优化技术,来学习新的、可解析和可推广的RL算法!
他们发现的其中两种算法可以推广到更复杂的环境中,比如具有视觉观察的Atari游戏。
这一成就使得RL算法越来越优秀!
具体怎么个“优秀法”,请看下文:
损失函数表示为计算图
首先,对于强化学习算法研究的难点,研究人员认为,一种可能的解决方案是设计一种元学习方法。
该方法可以设计新的RL算法,从而自动将其推广到各种各样的任务中。
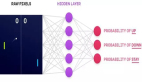
受神经架构搜索(NAS)在表示神经网络结构的图空间中搜索的思想启发,研究人员通过将RL算法的损失函数表示为计算图(computational graph)来元学习RL算法。
其中使用有向无环图来表示损失函数,该图带有分别表示输入、运算符、参数和输出的节点。
该表示方法好处有很多,总的来说就是可用来学习新的、可解析和可推广的RL算法。
并使用PyGlove库实现这种表示形式。
基于进化的元学习方法
接下来,研究人员使用基于进化的元学习方法来优化他们感兴趣的RL算法。
其过程大致如下:
新提出的算法必须首先在障碍环境中表现良好,然后才能在一组更难的环境中进行训练。算法性能被评估并用于更新群体(population),其中性能更好的算法进一步突变为新算法。在训练结束时,对性能最佳的算法在测试环境中进行评估。
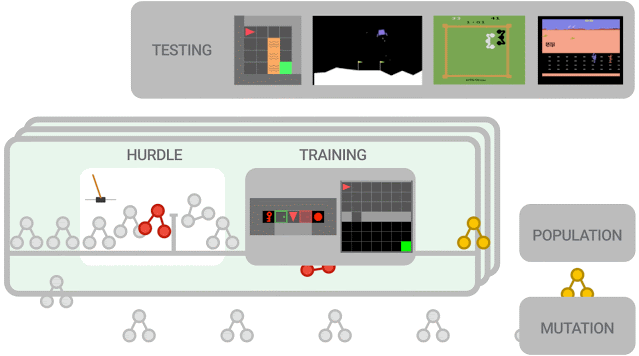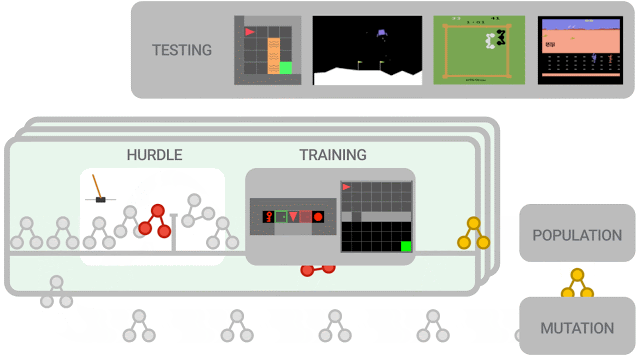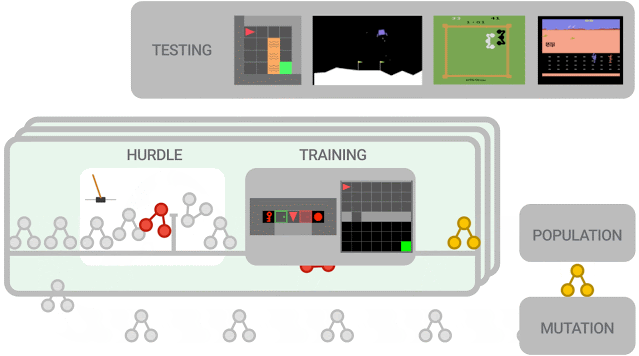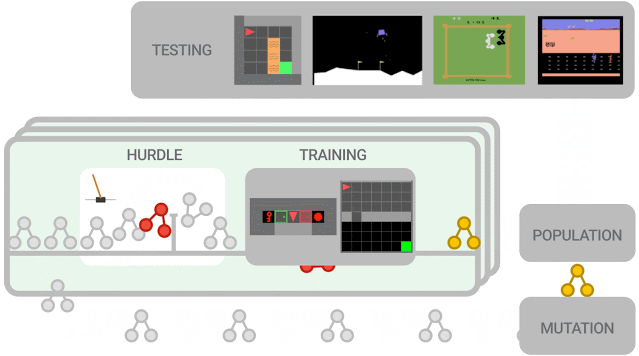
本次实验中的群体(population)规模约为300个智能体,研究人员观察到在2-5万个突变后,发现候选损失函数的进化需要大约3天的训练。
为了进一步控制训练成本,他们在初始群体中植入了人类设计的RL算法,eg. DQN(深度Q学习算法)。
发现两种表现出良好泛化性能的算法
最终,他们发现了两种表现出良好泛化性能的算法:
一种是DQNReg,它建立在DQN的基础上,在Q值上增加一个加权惩罚(weighted penalty),使其成为标准的平方Bellman误差。
第二种是DQNClipped,尽管它的支配项(dominating term)有一个简单的形式——Q值的最大值和平方Bellman误差(常数模),但更为复杂。
这两种算法都可以看作是正则化Q值的一种方法,都以不同的方式解决了高估Q值这一问题。
最终DQNReg低估Q值,而DQNClipped会缓慢地接近基本事实,更不会高估。
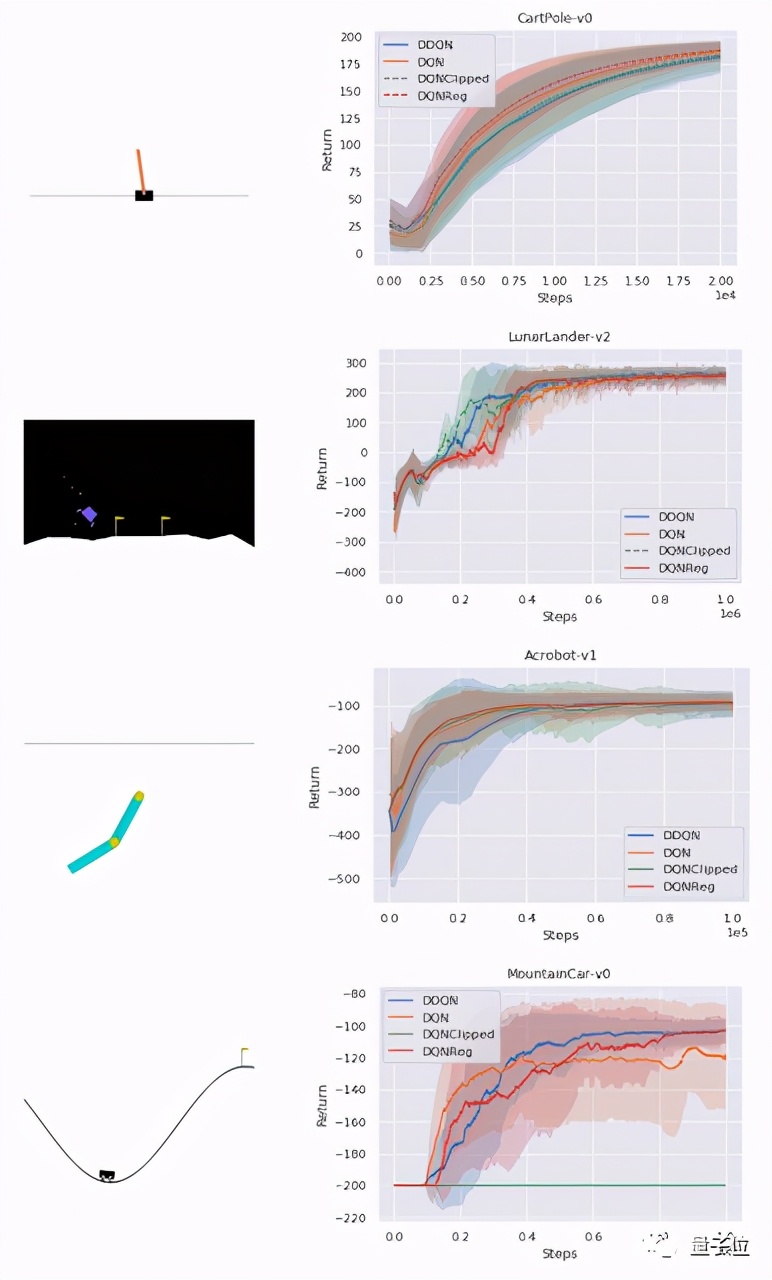
性能评估方面,通过一组经典的控制环境,这两种算法都可以在密集奖励任务(CartPole、Acrobot、LunarLander)中持平基线,在稀疏奖励任务(MountainCar)中,性能优于DQN。
其中,在一组测试各种不同任务的稀疏奖励MiniGrid环境中,研究人员发现DQNReg在训练和测试环境中的样本效率和最终性能都大大优于基线水平。
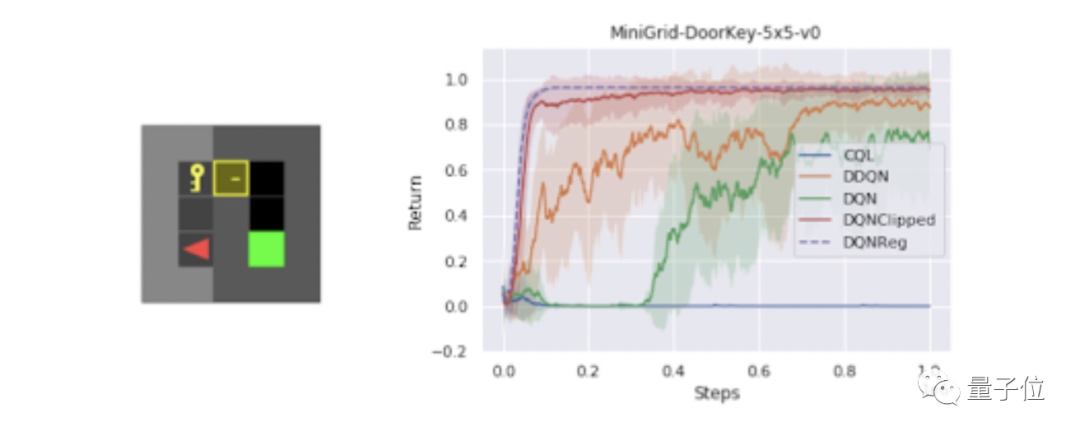
另外,在一些MiniGrid环境将DDQN(Double DQN)与DQNReg的性能进行可视化比较发现,当DDQN还在挣扎学习一切有意义的行为时,DQNReg已经可以有效地学习最优行为了。
最后,即使本次研究的训练是在基于非图像的环境中进行的,但在基于图像的Atari游戏环境中也观察到DQNReg算法性能的提高!
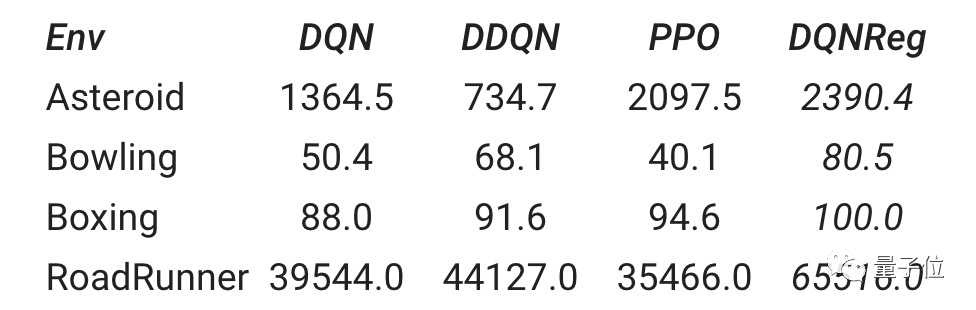
这表明,在一组廉价但多样化的训练环境中进行元训练,并具有可推广的算法表示,可以实现根本的算法推广。
此研究成果写成的论文,已被ICLR 2021接收,研究人员门未来将扩展更多不同的RL设置,如Actor-Critic算法或离线RL。