一、数组基础
1.1 定义
数组(Array)是一种线性表数据结构,它用一组连续的内存空间来存储一组具有相同类型的数据。
1.2 创建流程
当我们在 java 中当创建一个数组时,会在内存中划分出一块 连续的内存,当有数据进入的时候会将数据 按顺序的存储在这块连续的内存中。当需要读取数组中的数据时,需要提供数组中的 索引,然后数组根据索引将内存中的数据取出来,返回给读取程序。
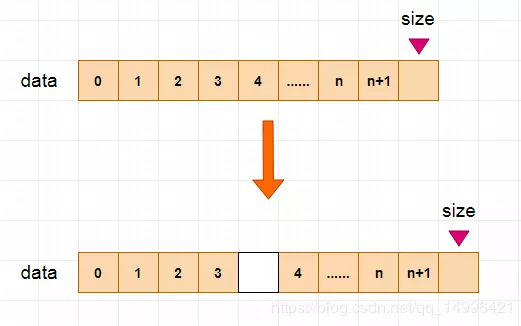
把数据码成一排进行存放:
所有的数据结构都支持几个基本操作:读取、插入、删除数组索引可以有语意,也可以没有语意,比如说 student[2],就代表是这个数组中的第三个学生。
因为数组在存储数据时是按顺序存储的,存储数据的内存也是连续的,所以数组最大的优点就是能够 快速查询,寻址读取数据比较容易,但是插入和删除就比较困难。
为什么数组最大的优点就是能够 快速查询。因为当我们在读取数据时,只需要告诉数组获取数据的索引位置就可以了,数组就会把对应位置的数据,读取出来
插入和 删除比较困难是因为这些存储数据的内存是连续的,数组大小固定,插入和删除都需要移动元素
例如:一个数组中编号 0>1>2>3>4这五个内存地址中都存了数组的数据,但现在你需要往4中插入一个数据,那就代表着从4开始,后面的所有内存中的数据都要往后移一个位置。
二、编写我们自己的数组类
我们知道想要维护某一个数据,我们需要对这个数据有这最基本的 增、删、改、查,这几个基本功能,所以我们自己手动编写的数组类,也是需要有用这几个最基本的功能,虽然不会像 List、Map这些类,那么强大,但是对于我们普通的开发来说,基本是可以满足,下图所示就是我们一个基本的数组类,那么我们是如何对数组进行改造,来编写一个属于我们自己的数组类的呢,这里我们以 增加和删除做重点讲解,本文中的所有源码会在最后贴出来,请往下看。
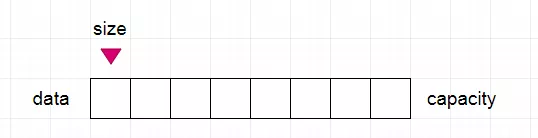
从上图中我们可以得知,我们创建数组类的时候,需要三个元素 data、size、capacity,而我们所需要使用的数组,肯定是要能够支持 多种数据类型,而不是单一的数据结构,因此,我们可以在设计类的时候,是需要加上泛型支持,让我们的数据结构可以支持放置 任何数据类型。
data:需要传递的数据size:元素中的个数capacity:数组的初始容量
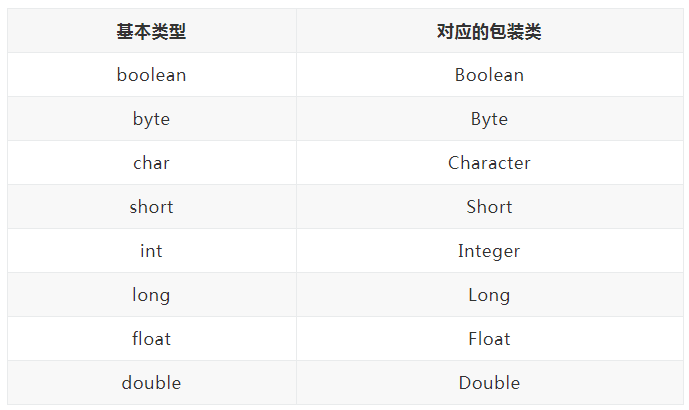
注意:我们上面所说的放置 任何数据类型,只能是类对象,不可以是基本数据类型,但是我们每个基本数据类型都有对应的包装类,所以我们的基本类型也是可以使用的,不过只是使用的是它的包装类
因此,我们在设计我们的数组类的时候,我们可以这么设计
- /**
- * @program:
- * @ClassName ArrayPlus
- * @description:
- * @author: lyy
- * @create: 2019-11-18 22:27
- * @Version 1.0
- **/
- public class ArrayPlus<E> {
- private E[] data;
- private int size;
- //构造函数,传入数组的容量capacity 构造array
- public ArrayPlus(int capacity){
- data = (E[])new Object[capacity];
- size = 0;
- }
- //无参数的构造函数,传入数组的容量capacity=10
- public ArrayPlus(){
- this(10);
- }
- //获取元素中的个数
- public int getSize(){
- return size;
- }
- //获取数组的容量
- public int getCapacity(){
- return data.length;
- }
- //返回数组是否为空
- public boolean isEmpty(){
- return size == 0;
- }
- @Override
- public String toString(){
- StringBuffer res = new StringBuffer();
- res.append(String.format("Array:Size = %d,capacity = %d\n",size,data.length));
- res.append("[");
- for (int i = 0; i < size; i++) {
- res.append(data[i]);
- if(i != size - 1)
- res.append(",");
- }
- res.append("]");
- return res.toString();
- }
- }
2.1 数组添加元素
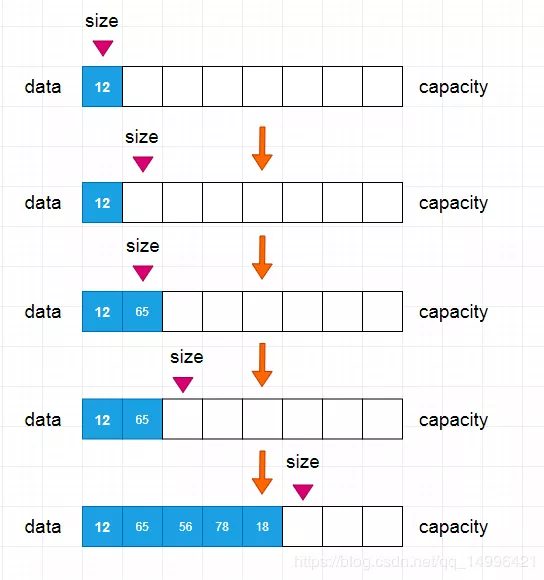
在数组中是如何添加数据的呢,首先我们需要创建一个 拥有初始容量的数组,当我们创建完成之后,size是指向第一个元素的,也就是 index=0的地方,当我们添加第一个数据后 也就是 data[0]=12后,我们的元素中的个数 size,需要往后挪一位的,也就是 size++的操作,每当我们操作一位,就需要将上面的操作重复执行,直到最后一个元素添加到我们的数组中。
如下图所示:
知道了怎么操作,但是我们要如果通过代码来完成呢?
首先我们要清楚在添加的时候, 在哪里?添加什么数据?,在哪里:我们要在数据的什么地方进行添加,也就是要添加到数组中的哪个下标—— index的地方,知道了在下标,我们只需要将添加的数据,添加到数组中为 index 的地方即可,除此之外,我们只需要对添加时,做一些基本的判断就可以了,代码如下:
- //在所有元素后添加一个新元素
- public void addLast(E e){
- add(size,e);
- }
- //想所有元素前添加一个新元素
- public void addFirst(E e){
- add(0,e);
- }
- //在第Index个位置插入一个新元素e
- public void add(int index,E e){
- if(size == data.length)
- throw new IllegalArgumentException("Add failed . Array is full.");
- if(index < 0 || index > size)
- throw new IllegalArgumentException("Add failed . Require index < 0 || index > size.");
- for (int i = size - 1; i >= index ; i--)
- data[i+1] = data[i];
- data[index] = e;
- size++;
- }
测试代码:
- public class Main2 {
- public static void main(String[] args) {
- ArrayPlus<Integer> arr = new ArrayPlus<>();
- for (int i = 12; i < 16; i++)
- arr.addLast(i);
- System.out.println(arr);
- }
- }
返回结果:
- Array:Size = 4,capacity = 10
- [12,13,14,15]
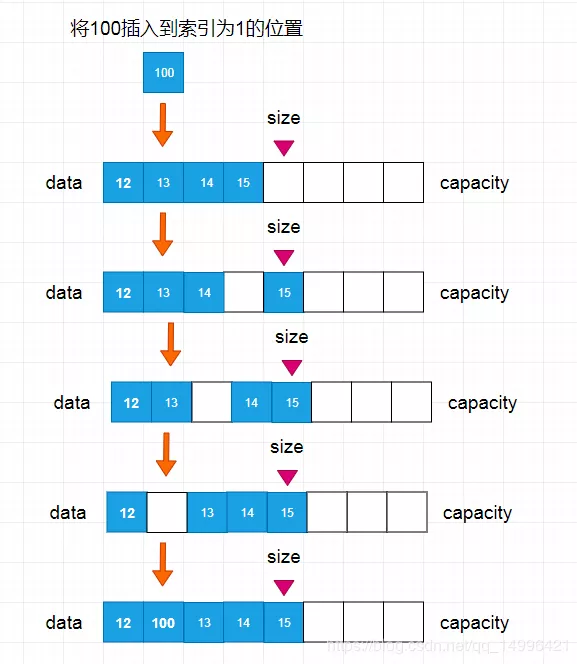
在数组中是如何执行插入呢?如下图所示:
测试代码:
- public static void main(String[] args) {
- ArrayPlus<Integer> arr = new ArrayPlus<>();
- for (int i = 12; i < 16; i++)
- arr.addLast(i);
- System.out.println(arr);
- arr.add(1,100);
- System.out.println(arr);
- }
返回结果:
- Array:Size = 4,capacity = 10
- [12,13,14,15]
- Array:Size = 5,capacity = 10
- [12,100,13,14,15]
2.2 数组删除元素
如果我们想要删除 索引为1的元素,是怎样操作的呢,首先我们需要先将 索引为2的数据,覆盖到 索引为1的元素上,再将 索引为3的数据放到 索引为2上,依次循环操作,直到最后一位元素,我们在将最后一位元素的数据设置为 null,这样垃圾回收机制就会自动帮我们清除这个元素。整个过程就完成了删除元素的功能,具体流程如下图所示:
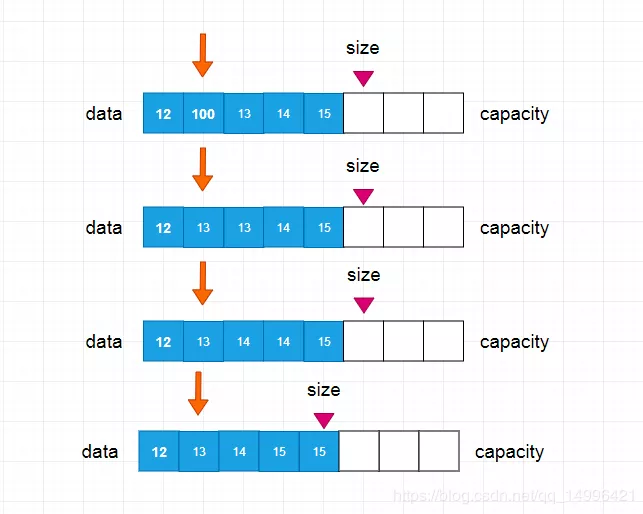
实现代码:
- //查找数组中元素e所在的索引,如果不存在元素e,则返回-1
- public int find(E e){
- for (int i = 0; i < size; i++) {
- if(data[i].equals(e))
- return i;
- }
- return -1;
- }
- //从数组中删除index位置的元素,返回删除的元素
- public E remove(int index){
- if(index < 0 || index >= size)
- throw new IllegalArgumentException("remove failed . Index is illegal.");
- E ret = data[index];
- for (int i = index+1 ; i < size; i++)
- data[i - 1] = data[i];
- size--;
- // loitering objects != memory leak
- data[size] = null;//如果一旦使用新的元素,添加新的对象就会覆盖掉
- return ret;
- }
- //从数组中删除第一个位置的元素,返回删除的元素
- public E removeFirst(){
- return remove(0);
- }
- //从数组中删除最后一个位置的元素,返回删除的元素
- public E removeLast(){
- return remove(size-1);
- }
- //从数组中删除元素e
- public void removeElement(E e){
- int index = find(e);
- if(index != -1)
- remove(index);
- }
测试:
- import com.bj.array.ArrayPlus;
- public class Main2 {
- public static void main(String[] args) {
- ArrayPlus<Integer> arr = new ArrayPlus<>();
- for (int i = 12; i < 16; i++)
- arr.addLast(i);
- System.out.println(arr);
- arr.add(1,100);
- System.out.println(arr);
- arr.remove(1);
- System.out.println(arr);
- }
- }
返回示例:
- Array:Size = 4,capacity = 10
- [12,13,14,15]
- Array:Size = 5,capacity = 10
- [12,100,13,14,15]
- Array:Size = 4,capacity = 10
- [12,13,14,15]
我们看到结果已经把索引为1的删除了,到这里我们已经完成了一大半了,还有一小点也是最重要的,就是当我们添加数据超过了我们的初始容量大小的时候,就会报错,初始容量,无法添加超过的数据,那么我们应该怎么操作呢?其实很简单,我们只需要给我们数组类,添加一个扩容的方法即可,当我们元素的个数等于数组长度的时候,我们就进行扩容,我们称之为 动态数组。
2.3 动态数组
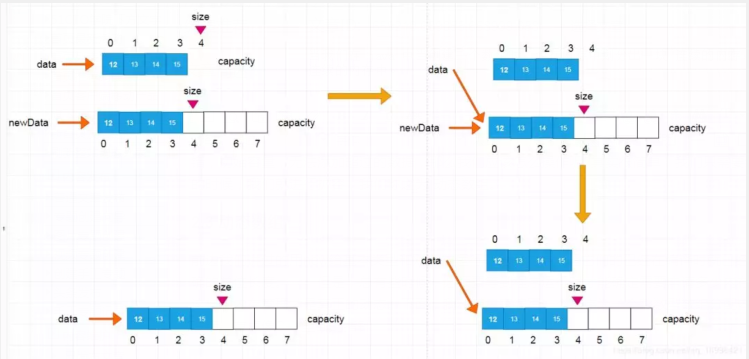
前边我们讲过的用new给基本类型和对象在运行时分配内存,但它们的已经在编译时就已经确定下来,因为我们为之申请内存的数据类型在程序里有明确的定义,有明确的单位长度。 但是,总有些时候,必须要等到程序运行时才能确定需要申请多少内存,甚至还需要根据程序的运行情况追加申请更多的内存。从某种意义上讲,这样的内存管理才是真正的动态。下面,我将带大家编写一个程序为一个整数型数组分配内存,实现动态数组。 当你们看到下面这个图的时候,有没有想到什么,没错,有点像C++里面的指针
实现代码:
- //在第Index个位置插入一个新元素e
- public void add(int index,E e){
- if(index < 0 || index > size)
- throw new IllegalArgumentException("Add failed . Require index < 0 || index > size.");
- if(size == data.length)
- resize(2 * data.length);
- for (int i = size - 1; i >= index ; i--)
- data[i+1] = data[i];
- data[index] = e;
- size++;
- }
- private void resize(int newCapacity) {
- E[] newData = (E[])new Object[newCapacity];
- for (int i = 0; i < size; i++)
- newData[i] = data[i];
- data = newData;
- }
动态数组测试:
- import com.bj.array.ArrayPlus;
- public class Main2 {
- public static void main(String[] args) {
- ArrayPlus<Integer> arr = new ArrayPlus<>();
- for (int i = 0; i < 10; i++)
- arr.addLast(i);
- System.out.println(arr);
- arr.add(1,100);
- System.out.println(arr);
- for (int i = 0; i < 6; i++)
- arr.remove(i);
- arr.removeLast();
- System.out.println(arr);
- }
- }
测试结果:
- Array:Size = 10,capacity = 10
- [0,1,2,3,4,5,6,7,8,9]
- Array:Size = 11,capacity = 20
- [0,100,1,2,3,4,5,6,7,8,9]
- Array:Size = 4,capacity = 10
- [100,2,4,6]
从结果中我们可以看到,当我们数组元素超过初始容量大小时,自动扩容到初始容量的 两倍也就是20,当我们数组长度小于1/4的时候,为什么是1/4的时候而不是1/2的时候呢,下面我们会做详细介绍。当我们数组长度小于1/4的时候,会自动缩回到初始10的容量,不会去占据大量的内存空间。
三、时间复杂度分析
3.1 基础
五种常见的时间复杂度 1) O(1):常数复杂度, 最快的算法,数组的存取是O(1) 1) O(n):线性复杂度, 例如:数组, 以遍历的方式在其中查找元素 1) O(logN):对数复杂度 1) O(nlogn):求两个数组的交集, 其中一个是有序数组,A数组每一个元素都要在B数组中进行查找操作,每次查找如果使用二分法则复杂度是 logN 1) O(n2):平方复杂度,求两个无序数组的交集
在这里,大O描述的是算法的运行时间和输入数据之间的关系
3.2 举例说明
大家可以看下面一个例子
- public static int sum(int[] nums){
- int sum = 0;
- for(int num: nums) sum += num;
- return sum;
- }
- 这个算法是 O(n) 复杂度的,其中 n是nums中的元素个数,算法和n呈线性关系
- 为什么说他是 O(n)的时间复杂度呢,因为这个算法运行的时间的多少是和 nums中元素的个数成线性关系的,那么这个线性关系,表现在我们的 n 是一次方,它不是 O(n) 方的,也不是 O(n) 的立方,n 对应的是一次方。
- 我们忽略常数,实际时间是:T=c1*n+c2c1:我们要把这个数据从 nums数组中取出来,其次我们还要把 sum这个数取出来,然后 num这个数和 sum相加,最终呢我们要这个结果扔回给 sum中c2:开始开辟了一个Int型的空间,我们把它叫 sum ,要把 0 初始化赋值给sum,在最终呢我们还要把这个 sum 给 return 回去
一方面把 c1 和 c2 具体分析出来是不大必要的,另一方面也是不太可能的,为什么说不可能呢?如果说把 num 从 nums 中取出来,基于 不同的语言,基于 不同的实现,它实际运行的 时间是不等的,就算转换成机器码,它对应的机器码的指令数也有可能是不同的,就算是指令数是相同的,同样的一个指令,在我们 cpu 的底层,你使用的 cpu 不同,很有可能,执行的操作也是不同的,所以在实际上我们可能说出 c1 是几条指令,但是却很难说出 c1 到底是多少,c2也是同理,正因为如此,我们在进行时间复杂度时,是忽略这些常数的。
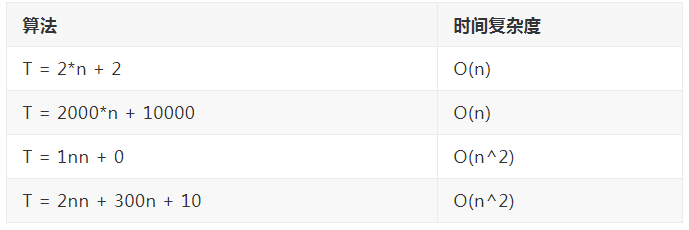
忽略这些常数就意味着什么,就意味着这些 t=2*n+2和t=2000*n+10000算法这些都是 O(n) 的算法,见下面列表:换句话说他们都是线性数据的算法,也就是说我们这个算法消耗的时间是和我们输入数据的规模成一个线性相关的, t=1*n*n+0也线性算法是和我们成平方关系的 ,他的性能比上面的差,因为他是 O(n^2)的
O(n)和O(n^2)并不代表说 O(n)的算法快于 O(n^2)的算法,我们要看 n 的常数,比如 n=3000的时候,或者 n>3000的时候, O(n^2)消耗的时间是远远大于 O(n)的,n越大 O(n)远远快于 O(n^2)O:描述的是一个算法,也就是说渐进时间复杂度当高阶项和低阶项同时出现的时候,低阶项会被忽略,比如说:T=2*n*n+300n+10当中 2*n*n,是 O(n^2)级别的算法,属于高阶项, 300n是 O(n)的算法低阶项,当n无穷大的时候,低阶项起的作用很小。
3.3 分析动态数组的时间复杂度
3.3.1 添加操作
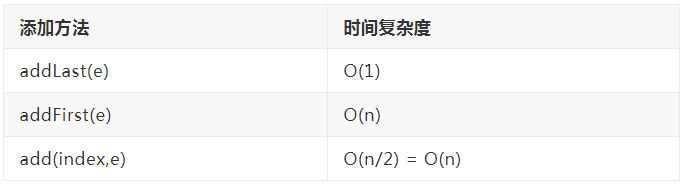
添加操作 总体来说属于 O(n) 级别的复杂度,如下列表
在程序设计中,我们要采用最严谨的设计,需要考虑到最坏的情况,所以我们说添加操作时属于 O(n)级别的复杂度,是因为我们在 addLast的时候,有可能会进行 resize的操作,我们从最坏的情况分析是对的,但是 addLast不可能每次都是进行 resize操作,比如 size 有十个,我们要添加十个元素后才会触发一个 resize,我们要在添加十个元素才会触发一个 resize,因此我们使用最坏情况进行分析的是不合理的,那么分析 addLast时间复杂度呢,请看下面小节。
3.3.2 resize的复杂度分析
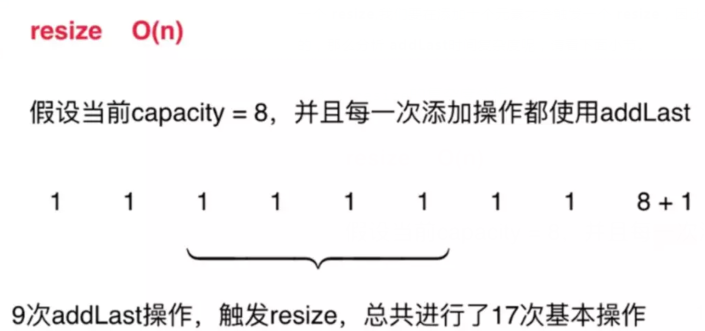
总共进行了17次基本操作:9次添加操作8次元素转移操作
- 9次addLast操作,触发resize,总共进行了17次基本操作,平均每次addLast操作,进行了2次基本操作
- 假设 capacity = n,n+1 次addLast,触发resize,总共进行了2n+1次基本操作,平均,每次addLast操作,进行了2次基本操作
- 这样均摊计算,时间复杂度是O(1)的,在这个例子里,这样均摊计算,比计算最坏情况有意义
- addLast 均摊复杂度是O(1)的,同理我们看 removeLast操作,均摊复杂度也是O(1)
3.3.3 复杂度震荡
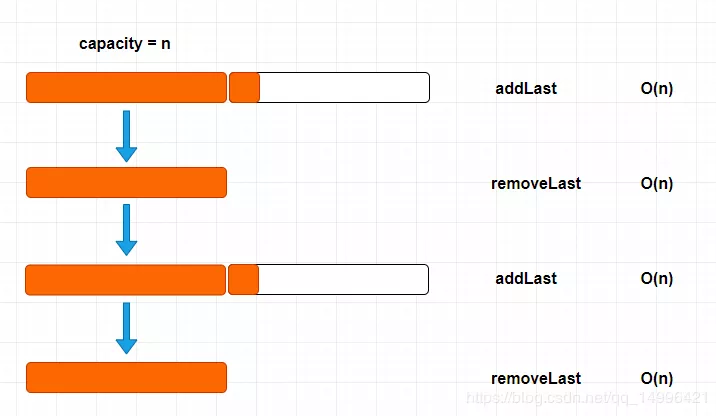
当我们数组容量满了的时候,因为是动态数组,回去自动扩容,我们又马上去remove 一个操作的时候,因为数组容量小于 初始容量的一半的时候,又会 自动 resize缩减为一半的大小,如此操作,就会一个问题,就是我们在 removeLast的时候 resize 过于着急(Eager)
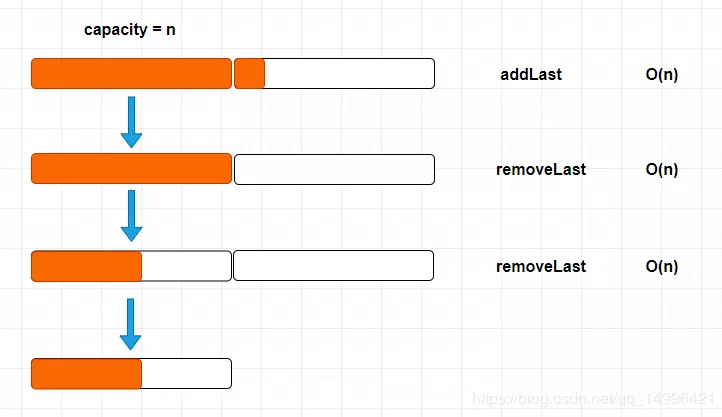
解决方案:Lazy,懒散的,其实也很简单,如下图所示:
当我们的 size == capacity /4 时候,才将capacity 减半,实现方式如下:
- //从数组中删除index位置的元素,返回删除的元素
- public E remove(int index){
- if(index < 0 || index >= size)
- throw new IllegalArgumentException("remove failed . Index is illegal.");
- E ret = data[index];
- for (int i = index+1 ; i < size; i++)
- data[i - 1] = data[i];
- size--;
- // loitering objects != memory leak
- data[size] = null;//如果一旦使用新的元素,添加新的对象就会覆盖掉
- if(size == data.length / 4 && data.length / 2 != 0)
- resize(data.length / 2);
- return ret;
- }
完整代码:
- package com.bj.array;
- /**
- * @program: Data-Structures
- * @ClassName Array
- * @description:
- * @author: lyy
- * @create: 2019-11-18 22:27
- * @Version 1.0
- **/
- public class ArrayPlus<E> {
- private E[] data;
- private int size;
- //构造函数,传入数组的容量capacity 构造array
- public ArrayPlus(int capacity){
- data = (E[])new Object[capacity];
- size = 0;
- }
- //无参数的构造函数,传入数组的容量capacity=10
- public ArrayPlus(){
- this(10);
- }
- //获取元素中的个数
- public int getSize(){
- return size;
- }
- //获取数组的容量
- public int getCapacity(){
- return data.length;
- }
- //返回数组是否为空
- public boolean isEmpty(){
- return size == 0;
- }
- //在所有元素后添加一个新元素
- public void addLast(E e){
- add(size,e);
- }
- //想所有元素前添加一个新元素
- public void addFirst(E e){
- add(0,e);
- }
- //在第Index个位置插入一个新元素e
- public void add(int index,E e){
- if(index < 0 || index > size)
- throw new IllegalArgumentException("Add failed . Require index < 0 || index > size.");
- if(size == data.length)
- resize(2 * data.length);
- for (int i = size - 1; i >= index ; i--)
- data[i+1] = data[i];
- data[index] = e;
- size++;
- }
- //获取index索引位置的元素
- public E get(int index){
- if(index < 0 || index >= size)
- throw new IllegalArgumentException("Get failed . Index is illegal.");
- return data[index];
- }
- //修改index索引位置的元素为e
- public void set(int index,E e){
- if(index < 0 || index >= size)
- throw new IllegalArgumentException("Set failed . Index is illegal.");
- data[index] = e;
- }
- //查找数组中是否有元素e
- public boolean contains(E e){
- for (int i = 0; i < size; i++) {
- if(data[i].equals(e))
- return true;
- }
- return false;
- }
- //查找数组中元素e所在的索引,如果不存在元素e,则返回-1
- public int find(E e){
- for (int i = 0; i < size; i++) {
- if(data[i].equals(e))
- return i;
- }
- return -1;
- }
- //从数组中删除index位置的元素,返回删除的元素
- public E remove(int index){
- if(index < 0 || index >= size)
- throw new IllegalArgumentException("remove failed . Index is illegal.");
- E ret = data[index];
- for (int i = index+1 ; i < size; i++)
- data[i - 1] = data[i];
- size--;
- // loitering objects != memory leak
- data[size] = null;//如果一旦使用新的元素,添加新的对象就会覆盖掉
- if(size == data.length / 4 && data.length / 2 != 0)
- resize(data.length / 2);
- return ret;
- }
- //从数组中删除第一个位置的元素,返回删除的元素
- public E removeFirst(){
- return remove(0);
- }
- //从数组中删除最后一个位置的元素,返回删除的元素
- public E removeLast(){
- return remove(size-1);
- }
- //从数组中删除元素e
- //思考?如果返回是否删除成功 2、如果存在重复数据,如何删除多个
- public void removeElement(E e){
- int index = find(e);
- if(index != -1)
- remove(index);
- }
- @Override
- public String toString(){
- StringBuffer res = new StringBuffer();
- res.append(String.format("Array:Size = %d,capacity = %d\n",size,data.length));
- res.append("[");
- for (int i = 0; i < size; i++) {
- res.append(data[i]);
- if(i != size - 1)
- res.append(",");
- }
- res.append("]");
- return res.toString();
- }
- private void resize(int newCapacity) {
- E[] newData = (E[])new Object[newCapacity];
- for (int i = 0; i < size; i++)
- newData[i] = data[i];
- data = newData;
- }
- }
有时候更"懒",会让我们的程序更方便点,我是牧小农,大家加油!