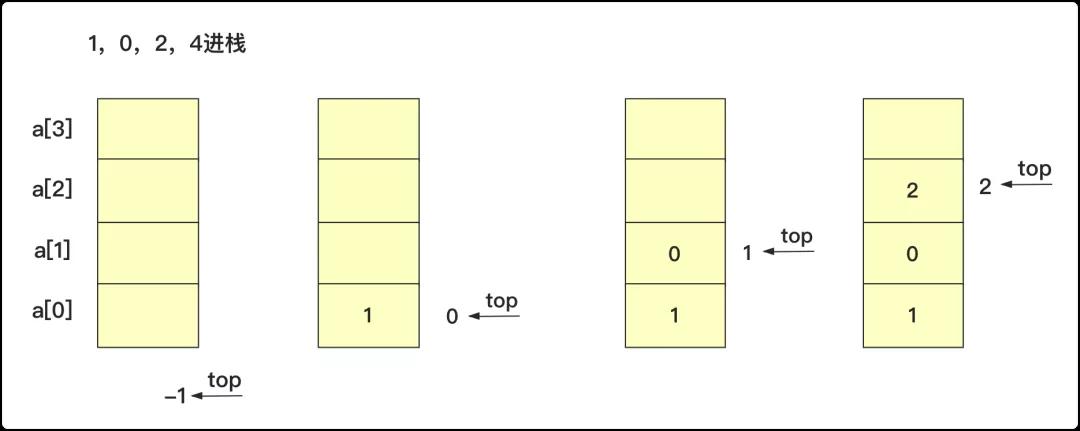
什么是栈
栈在我们日常编码中遇到的非常多,很多人对栈的接触可能仅仅局限在 递归使用的是栈 和 StackOverflowException,栈是一种后进先出的数据结构(可以想象生化金字塔的牢房和生化角斗场的狗洞)。栈,简单而又不简单,是因为直接学习栈比较容易,但使用栈解决问题很多时候需要巧妙的方法。
本文着重讲解栈数据结构的设计与实现,然后在文末补充两道栈非常非常经典的问题!一定要会!
勾起一波回忆
栈是这么定义的:
栈(stack)又名堆栈,它是一种运算受限的线性表。限定仅在表尾进行插入和删除操作的线性表。这一端被称为栈顶,相对地,把另一端称为栈底。向一个栈插入新元素又称作进栈、入栈或压栈,它是把新元素放到栈顶元素的上面,使之成为新的栈顶元素;从一个栈删除元素又称作出栈或退栈,它是把栈顶元素删除掉,使其相邻的元素成为新的栈顶元素。
稍微介绍一下关键名词:
运算受限:也就是这个表你不能随便的删除插入。只能按照它的规则进行插入删除。比如栈就只能在一端进行插入和删除。同样,队列也是运算受限,只能在两头操作。
线性表:栈也是一种线性表,前面详细介绍过线性表,它表达的是一种数据的逻辑关系。也就是在栈内各个元素是相邻的。当然在具体实现上也分数组和链表实现,他们的物理存储结构不同。但是逻辑结构(实现的目的)相同。
栈顶栈底: 这个描述是偏向于逻辑上的内容,因为大家知道数组在末尾插入删除更容易,而单链表通常在头插入删除更容易。所以数组可以用末尾做栈顶,而链表可以头做栈顶。
栈的应用: 栈的应用广泛,比如你的程序执行查看调用堆栈、计算机四则加减运算、算法的非递归形式、括号匹配问题等等。所以栈也是必须掌握的一门数据结构。最简单大家都经历过,你拿一本书上下叠在一起,就是一个后进先出的过程,你可以把它看成一个栈。下面我们介绍数组实现的栈和链表实现的栈。
数组实现
数组实现的栈用的比较多,我们经常刷题也会用数组去实现一个简单的栈去解决简单的问题。
结构设计
对于数组来说,我们模拟栈的过程很简单,因为栈是后进先出,我们很容易在数组的末尾进行插入和删除。所以我们选定末尾为栈顶。所以对于一个栈所需要的基础元素是 一个data[]数组和一个top(int)表示栈顶位置。
那么初始化函数代码为:
- private T data[];
- private int top;
- public seqStack() {
- data=(T[]) new Object[10];
- top=-1;
- }
- public seqStack(int maxsize)
- {
- data=(T[]) new Object[maxsize];
- top=-1;
- }
push插入
栈的核心操作之一push():入栈操作。
- 如果top<数组长度-1。入栈,top++;a[top]=value;
- 如果top==数组长度-1;栈满。
pop弹出并返回首位
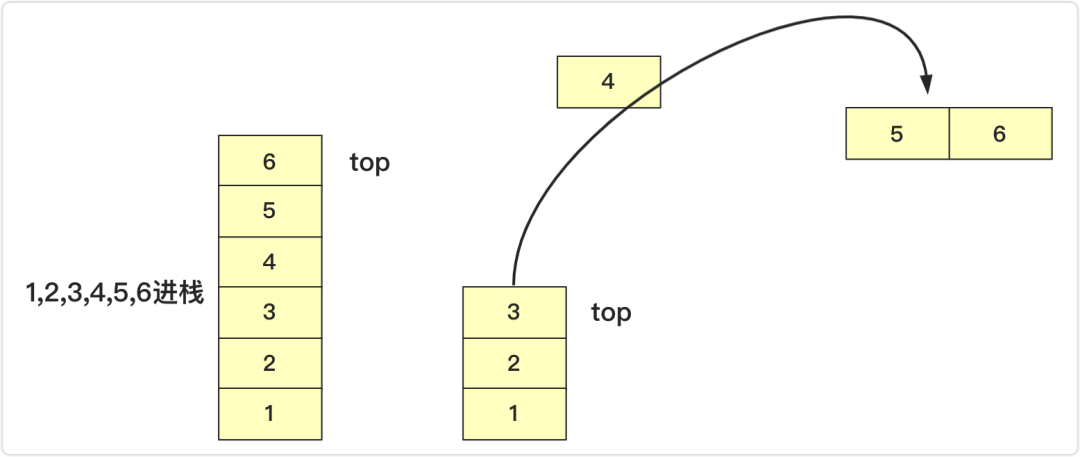
如果top>=0,栈不为空,可以弹出。return data[top--];
如下图,本来栈为1,2,3,4,5,6(栈顶),执行pop操作,top变为3的位置并且返回4;
其他操作
例如peek操作时返回栈顶不弹出.所以只需满足要求时候return data[top]即可。
数组实现:
- package 队栈;
- public class seqStack<T> {
- private T data[];
- private int top;
- public seqStack() {
- data=(T[]) new Object[10];
- top=-1;
- }
- public seqStack(int maxsize)
- {
- data=(T[]) new Object[maxsize];
- top=-1;
- }
- boolean isEmpty()
- {
- return top==-1;
- }
- int length()
- {
- return top+1;
- }
- boolean push(T value) throws Exception//压入栈
- {
- if(top+1>data.length-1)
- {
- throw new Exception("栈已满");
- }
- else {
- data[++top]=value;
- return true;
- }
- }
- T peek() throws Exception//返回栈顶元素不移除
- {
- if(!isEmpty())
- {
- return data[top];
- }
- else {
- throw new Exception("栈为空");
- }
- }
- T pop() throws Exception
- {
- if(isEmpty())
- {
- throw new Exception("栈为空");
- }
- else {
- return data[top--];
- }
- }
- public String toString()
- {
- if(top==-1)
- {
- return "";
- }
- else {
- String va="";
- for(int i=top;i>=0;i--)
- {
- va+=data[i]+" ";
- }
- return va;
- }
- }
- }
链表实现
有数组实现,链表当然也能实现。对于栈的设计,大致可以分为两种思路:
- 像数组那样在尾部插入删除。大家都知道链表效率低在查询,而查询到尾部效率很低,就算用了尾指针,可以解决尾部插入效率,但是依然无法解决删除效率(删除需要找到前驱节点),还需要双向链表。前面虽然详细介绍过双向链表,但是这样未免太复杂!
- 所以我们采用带头节点的单链表在头部插入删除,把头当成栈顶,插入直接在头节点后插入,删除也直接删除头节点后第一个节点即可,这样就可以完美的满足栈的需求。
结构设计
设计上和链表很相似,长话短说,短话不说,直接上代码就懂。
链表的节点:
- static class node<T>
- {
- T data;
- node next;
- public node() {
- }
- public node(T value)
- {
- this.data=value;
- }
- }
基本结构:
- public class lisStack <T>{
- int length;
- node<T> head;//头节点
- public lisStack() {
- head=new node<>();
- length=0;
- }
- //其他方法
- }
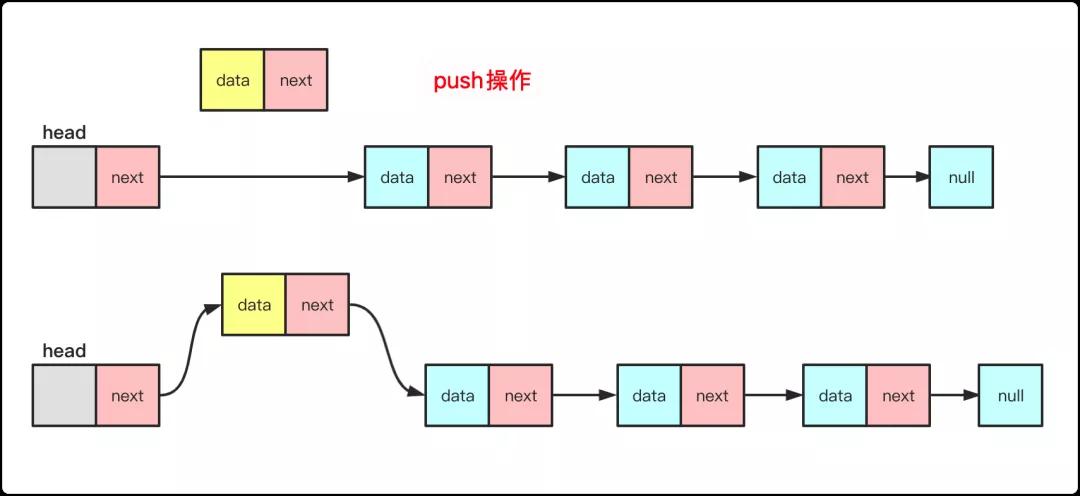
push插入
与单链表头插入一致,如果不太了解可以看看前面写的线性表有具体讲解过程。
和数组形成的栈有个区别,链式实现的栈理论上栈没有大小限制(不突破内存系统限制),不需要考虑是否越界,而数组则需要考虑容量问题。
如果一个节点team入栈:
- 空链表入栈head.next=team;
- 非空入栈team.next=head.next;head.next=team;
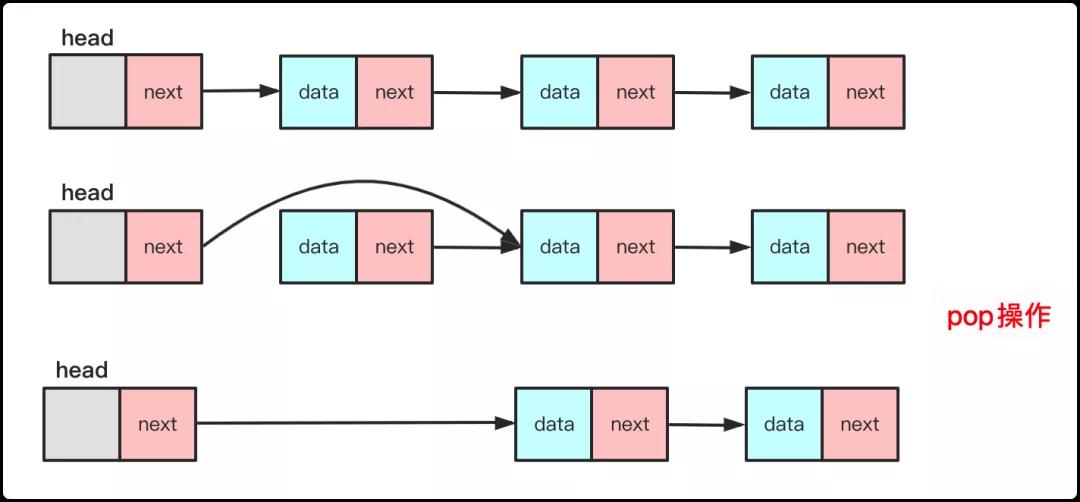
pop弹出
与单链表头删除一致,如果不太了解请先看笔者对线性表介绍的。
和数组同样需要判断栈是否为空,如果节点team出栈:head指向team后驱节点。
其他操作
其他例如peek操作时返回栈顶不弹出.所以只需判空满足题意时候return head.next.data即可。而length你可以遍历链表返回长度,也可以动态设置(本文采取)跟随栈长变化。
链表实现:
- package 队栈;
- public class lisStack <T>{
- static class node<T>
- {
- T data;
- node next;
- public node() {
- }
- public node(T value)
- {
- this.data=value;
- }
- }
- int length;
- node<T> head;//头节点
- public lisStack() {
- head=new node<>();
- length=0;
- }
- boolean isEmpty()
- {
- return head.next==null;
- }
- int length()
- {
- return length;
- }
- public void push(T value) {//近栈
- node<T> team=new node<T>(value);
- if(length==0)
- {
- head.next=team;
- }
- else {
- team.next=head.next;
- head.next=team;}
- length++;
- }
- public T peek() throws Exception {
- if(length==0) {throw new Exception("链表为空");}
- else {//删除
- return (T) head.next.data;
- }
- }
- public T pop() throws Exception {//出栈
- if(length==0) {throw new Exception("链表为空");}
- else {//删除
- T value=(T) head.next.data;
- head.next=head.next.next;//va.next
- length--;
- return value;
- }
- }
- public String toString(){
- if(length==0) {return "";}
- else {
- String va="";
- node team=head.next;
- while(team!=null)
- {
- va+=team.data+" ";
- team=team.next;
- }
- return va;
- }
- }
- }
栈能这么玩
既然上面详细讲解设计栈,这里来两道栈非常经典非常经典的例题(非常高频,很容易忘,又很重要,普通问题就不放的)
力扣20有效的括号:
题意:给定一个只包括 '(',')','{','}','[',']' 的字符串,判断字符串是否有效。
有效字符串需满足:
左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。
注意空字符串可被认为是有效字符串。
示例 :
输入: "()[]{}"
输出: true
示例 :
输入: "([)]"
输出: false
分析:
括号类的问题是经典栈类问题,肯定要想到用栈处理。判断一个字符串满不满足一个有效的字符串,就要看它是不是都能组成对。
从单个括号对来说,((,))都是不满足的,只有()才可满足,即一左一右。
从多个括号对来说 {[(字符串还可接受任意无限(,[,{的括号。但是如果向左的括号只能先接收)括号(变成{[)。
从上面可以看作一种相消除的思想。例如(({[()()]}))字符串遍历时候可以这样处理:
- (({[(下一个)消掉成(({[
- (({[(下一个)消掉成(({[
- (({[下一个]消掉成(({
- (({下一个}消掉成((
- ((下一个)消掉成(
- (下一个)消掉成 这样就满足题意
每次操作的时候都判断剩余有效括号最顶部那个括号是否能够和遍历的相消除,这个过程利用栈判断当前是加入栈还是消除顶部,到最后如果栈为空说明满足,否则不满足,当然具体括号要对应,具体实现代码为:
- public boolean isValid(String s) {
- Stack<Character>stack=new Stack<Character>();
- for(int i=0;i<s.length();i++)
- {
- char te=s.charAt(i);
- if(te==']')
- {
- if(!stack.isEmpty()&&stack.pop()=='[')
- continue;
- else {
- return false;
- }
- }
- else if(te=='}')
- {
- if(!stack.isEmpty()&&stack.pop()=='{')
- continue;
- else {
- return false;
- }
- }
- else if(te==')')
- {
- if(!stack.isEmpty()&&stack.pop()=='(')
- continue;
- else {
- return false;
- }
- }
- else
- stack.push(te);
- }
- return stack.isEmpty();
- }
当然,JDK自带的栈用起来不快,可以用数组优化:
- public boolean isValid(String s) {
- char a[]=new char[s.length()];
- int index=-1;
- for(int i=0;i<s.length();i++)
- {
- char te=s.charAt(i);
- if(te==']')
- {
- if(index>=0&&a[index]=='[')
- index--;
- else {
- return false;
- }
- }
- else if(te=='}')
- {
- if(index>=0&&a[index]=='{')
- index--;
- else {
- return false;
- }
- }
- else if(te==')')
- {
- if(index>=0&&a[index]=='(')
- index--;
- else {
- return false;
- }
- }
- else
- a[++index]=te;
- }
- return index==-1;
- }
力扣32最长有效括号(困难)
题目描述:给定一个只包含 '(' 和 ')' 的字符串,找出最长的包含有效括号的子串的长度。
示例 :
- 输入: "(()"
- 输出: 2
- 解释: 最长有效括号子串为 "()"
示例 :
- 输入: ")()())"
- 输出: 4
- 解释: 最长有效括号子串为 "()()"
方案一暴力
这种题核心思想就是使用栈模拟。本题的话更简单一点因为只有(和)两种括号,使用暴力的时候就可以循环每次找到最长的有效括号。而括号匹配的时候可以直接终止的情况是)右括号多出无法匹配。
例如())(到第三个不可能和前面相连。如果来(只需要期待后面能够来),一个)可以和一个(组成一对,消除栈中的一个(。
当然,在具体的实现上,我们用数组模拟栈,实现代码为:
- public int longestValidParentheses(String s) {
- char str[]=s.toCharArray();//字符数组
- int max=0;
- for(int i=0;i<str.length-1;i++)
- {
- int index=-1;
- if(max>=str.length-i)
- break;
- for(int j=i;j<str.length;j++)
- {
- if(str[j]=='(')
- index++;
- else {
- if(index<0)
- {
- i=j;
- break;
- }
- else {
- index--;
- }
- }
- if(index==-1&&(j-i+1>max))
- {
- max=j-i+1;
- }
- }
- }
- return max;
- }
这个复杂度太高,我们看看如何用栈优化。
方案二栈优化
如何将这道题从一个O(n2)的时间复杂度优化到O(n)?很容易, 我们需要注意他的过程。我们先随便看几个可能的最大情况。
- ( ) ) ( ) ( ( ) ( ) ) 最大为后面部分(空格分开)
- ( ) ( ) ( ( ( ) 最大为前面部分
- ( ( ( ( ( ( ) ( ) ( ) ( ) 最大为后面部分
对于这么一次获取你会发现不同括号会有些区别:
(:左括号一旦出现那么他就期待一个)进行匹配,但它的后面可能有)并且在这中间有很多其他括号对。
):右扩号有两种情况:
- 一种是当前已经超过左括号前面已经不可能连续了。例如( ) ) ( )第三个括号出现已经使得整个串串不可能连续,最大要么在其左面,要么在其右面。 你可以理解其为一种清零初始机制。
- 另一种情况)就是目标栈中存在(可与其进行匹配。匹配之后要叠加到消除后平级的数量上,并且判断是否是最大值。(下面会解释)
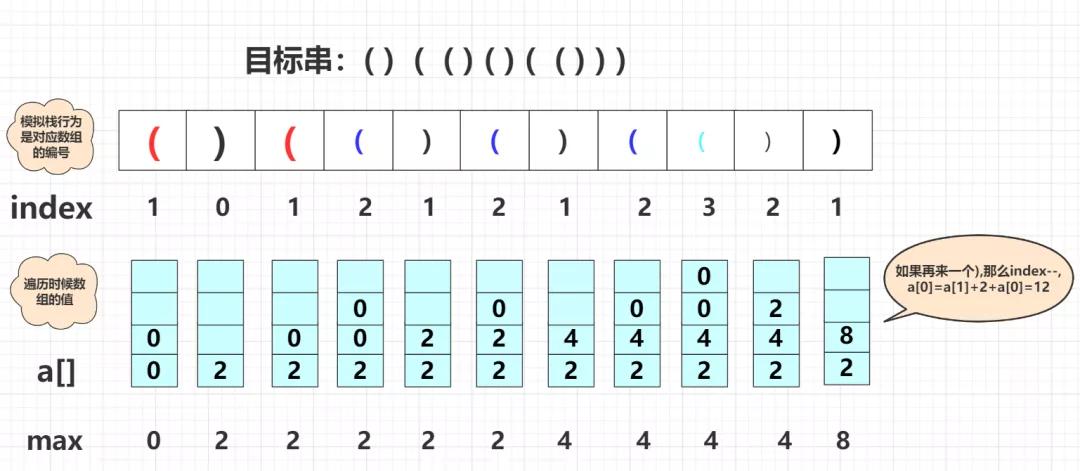
在具体实现的思路上,就是使用一个int数组标记当前层级(栈深)有正确的括号数量。模拟一次栈行为从左向右,遇到)太多(当前栈中不存在(进行匹配)就将数据清零重新开始。这样一直到最后。你可以把它看成台阶,遇到(就上一个台阶并清零该新台阶,遇到)就下一个台阶并且把数量加到下降后的台阶上。具体可以看下面图片模拟的过程:
( ) ( ( ) ( ) ( ( ) ) )
仔细看看这张图,具体实现代码为:
- public static int longestValidParentheses(String s) {
- int max=0;
- int value[]=new int[s.length()+1];
- int index=0;
- for(int i=0;i<s.length();i++)
- {
- if(s.charAt(i)=='(')
- {
- index++;
- value[index]=0;
- }
- else {//")"
- if(index==0)
- {
- value[0]=0;
- }
- else {
- value[index-1]+=value[index--]+2;//叠加
- if(value[index]>max)//更新
- max=value[index];
- }
- }
- }
- return max;
- }
用栈也可以实现,但是效率比数组略低:
- public int longestValidParentheses(String s) {
- int maxans = 0;
- Stack<Integer> stack = new Stack<>();
- stack.push(-1);
- for (int i = 0; i < s.length(); i++) {
- if (s.charAt(i) == '(') {//(将当前的
- stack.push(i);
- } else {
- stack.pop();
- if (stack.empty()) {
- stack.push(i);
- } else {//i-stack.peek就是i是出现的总个数 peek是还没匹配的个数
- maxans = Math.max(maxans, i - stack.peek());
- }
- }
- }
- return maxans;
- }
总结
到这里,本文对栈的介绍就结束了,相信你可以手写个栈并且可以小试牛刀解决括号匹配问题!当然栈能解决的问题还有很多比如接雨水问题、二叉树非递归遍历等等,有些重要的还会再总结。