2019 年,日本东北大学和普渡大学的研究者进行了一个概念证明实验,用「概率比特」代替量子比特解决困扰经典计算机的整数分解问题。相关研究发表在《Nature》杂志上,证明了一种名为「概率计算机」的装置的可行性。作者表示,这种「概率计算机」可以解决一些通常认为需要依靠量子计算机解决的问题,但建造的条件没有那么苛刻(可在室温下运行),因此实现起来可能更加容易,他们还将「概率比特」称为「穷人的量子比特」。最近,该研究的作者又在《IEEE Spectrum》上发表了一篇短文,用通俗的语言介绍了这种计算机的基本原理。
近年来,随着摩尔定律走向消亡,量子计算机被人们寄予厚望。许多评论者指出,如果工程人员能够设计出实用的量子计算机,人类的计算方式将发生结构式转变。
但是,这一断言有个重要的「如果」。
从理论上来说,量子计算机前景广阔,但建造一台实用的量子计算机需要克服巨大的困难。一些怀疑者甚至认为,由于技术难度过大,人们可能无法在可预见的未来建造出一台通用量子计算机。当然,也有人比较乐观,认为只要花 5-10 年就能实现这一愿景,这些人来自谷歌、IBM、英特尔等正在建造量子计算机的科技巨头。
但是,即使整个量子计算产业的发展比支持者预期的要慢很多,有一件事似乎是确定的。量子计算已经激发了人们对概率在计算系统中所扮演角色的深刻理解——正如已故物理学家理查德 · 费曼在上世纪 80 年代将这一想法重新带回人们视野时所期望的那样。
在 2012 年开始着手概率比特(p-bit)的研究时,我们寻求的正是这种理解。「概率比特」是基于量子比特(qubit)起的一个名字。费曼曾将这种这种概率计算机视为他所展望的量子计算机的一种对比。因此,我们问了自己一个问题:怎么才能造一个出来?
有两个磁化方向的磁体可以存储一个比特。早期的计算机使用这种方法造出了磁芯存储器。然而,将磁芯存储器变小是非常困难的,因为它的体积越小,性质就越不稳定。
在 2019 年的一篇《Nature》论文中,我们成功利用了这个看起来像 bug 的特点,使用不稳定的小磁体来实现 p-bit。在日本东北大学研究者的帮助,我们构建了一台有 8 个 p-bit 的概率计算机。

这种新的基于磁体的 p-bit 在建造概率计算机时并不是必需的。其实,早些时候,我们已经构建了一种利用复杂电子电路从确定性比特中产生伪随机序列以实现 p-bit 的概率计算机。富士通等公司也已经开始销售类似的概率计算机。但是,使用不稳定的磁体作为基本构建块,我们就可以用几个晶体管(而不是几千个)来实现一个 p-bit,这使得大型概率计算机的构建成为可能。
在这样一台计算机中,p-bit 组成的系统从初始状态演化到最终状态,并通过许多可能的中间状态之一。计算机走哪条路径完全是一种偶然,每条路径都有一定的概率。把所有可能路径的概率加起来,你就得到了到达一个给定最终状态的总概率。
量子计算机也做类似的事情,但它用的是量子比特,而不是概率比特。这就意味着,这里每条路径都有物理学家所说的概率振幅,它可以是负的。更准确地说,它是一个复数,既有实部也有虚部。
在量子计算机中,要想确定从某个初始状态到最终状态的总体概率,你首先要把所有可能路径的振幅相加,得到最终状态的概率振幅。最终的振幅也是一个复数,然后求其大小的平方得到实际概率,这个数字介于 0 和 1 之间。
简而言之,这就是概率计算机和量子计算机之间的关键区别。前者将所有概率加起来,后者将复数概率振幅加起来。
这种差异其实非常重要。概率是一个小于 1 的正数,所以加上一个额外的路径只会提高最终概率。但概率振幅是复数,这就意味着增加一个额外的路径可能会抵消一个现有的路径。这就好像一条路径有一个负的概率。
量子计算的力量直接来自这种使概率为负的能力。用于整数分解的 Shor 以及用于数据搜索的 Grover 等知名算法都会小心翼翼地编排可用的中间路径,以确保那些导致错误输出的路径被抵消,而那些通往正确答案的路径可以被添加。
但是,这一力量的实现是要付出代价的。携带这些复数振幅的量子比特必须被小小翼翼地保护,以免受环境的影响。这通常需要极低的温度。相比之下,在室温下使用更简单的技术就可以创建概率计算机。但这样的计算缺乏负概率的魔力,因此只对不需要路径抵消的算法有效。
用概率比特模拟量子计算机在理论上是可能的,但这并不是一个实用的策略。尽管如此,与确定性计算机相比,概率计算机还是能在很多重要问题上提供显著加速,这就是为什么我们对建造这种计算机如此感兴趣。
概率计算机如何工作?其实,它的原理和我们日常使用的数字系统非常不同,甚至大多数计算机工程专业的学生都对此知之甚少。因此,我们想以对话的方式聊一聊这个话题。
对话人物的名字取自伽利略的一本书——《两种世界体系的对话》。这是一本写得很机智的书,书中内容以三个人物的对话展开——Simplicio(主张地心说的亚里士多德主义者)、Salviati(主张日心说的哥白尼主义者)和 Sagredo(在这场辩论中持中立态度的博学智者)。在这场对话中,Salviati 系统地驳斥了 Simplicio 的所有观点,并得出了伽利略所主张的关于地球围绕太阳运转的证明。Sagredo 最终总结道,睿智的 Salviati(其实就是伽利略本人在书中的投影)是正确的。亚里士多德错了。然后三人退下,享受餐点和美酒。
本文的对话也在这三人之间展开,只是角色的使命略有变化。Salviati 负责传达作者的知识和观点;Sagredo 可以看成读者(你);Simplicio 只是路人甲。三人在飞机上相遇。
以下是对话部分:
什么是「概率计算机」
Sagredo:我看你在读 IEEE 杂志,你是电气工程师吗?
Salviati:是啊,我是研究计算的。
Sagredo:你最近在忙什么有趣的事情吗?
Salviati:我和我的同事在研究一种新的计算方法。你知道,我们的所有电子设备,比如手机,都是基于电路的,每个输入都有对应的输出,比如输入 5 和 6,这些设备就可以给出它们相乘的结果 30。但现在,我们构建了一个反向的电路:给一个数字 30,设备可以给出你所有的输入组合,比如 5 和 6、15 和 2、10 和 3 以及 30 和 1。
Sagredo:听起来很有意思。但这是做什么用的?
Salviati:它有很多用途,因为现在很多问题反过来都会变得很难,比如乘法计算就比因式分解简单得多。很多小孩都可以迅速算出 711 x 85 等于 65535,但把 65535 分解为 711 x 85 就没那么简单了,进一步得到其他组合(比如 257 x 255)就更难了。
Sagredo:我明白了。但是我听说现在的计算机都能打败围棋大师,那解决这类问题也不难吧?
Salviati:的确,现在的数字计算机可以打败围棋大师,但鲜为人知的是,它们要消耗 10 兆瓦的电才能做到这一点,而人类围棋大师只需要消耗 10 到 20 瓦。人们对降低复杂计算的能耗非常感兴趣,我们认为我们正在研究的「反向计算」可以实现这一愿景。
Sagredo:您应该很难向我这种小白解释你们的设计理念吧?
Salviati:确实得多花点时间,我需要画几张画。(Salviati 看到旁边的人有张没用过的餐巾纸。)不好意思,可以用一下您的餐巾纸吗?
Simplicio:没问题。
Salviati:(Salviati 放下小桌板开始画画。)你看,在数字计算机中,所有的东西都能用比特(0 和 1)来表示,后者又可以用拥有两种状态的物理实体来表示,比如磁铁。
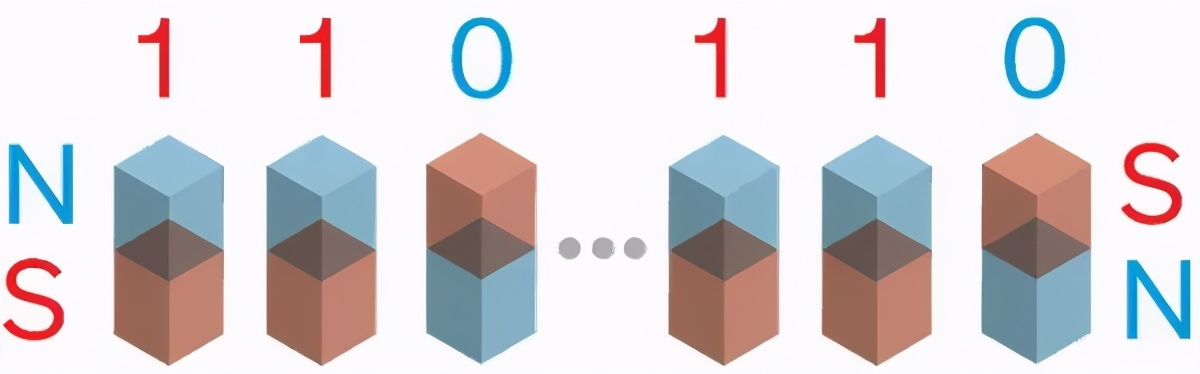
工程师们制造复杂的电路来执行特定的操作。比如,我们可以构造一个电路来做一比特二进制乘法运算:输出的比特是 0 或 1(我们称它为 C),具体结果取决于输入比特 A 和 B 的乘积。
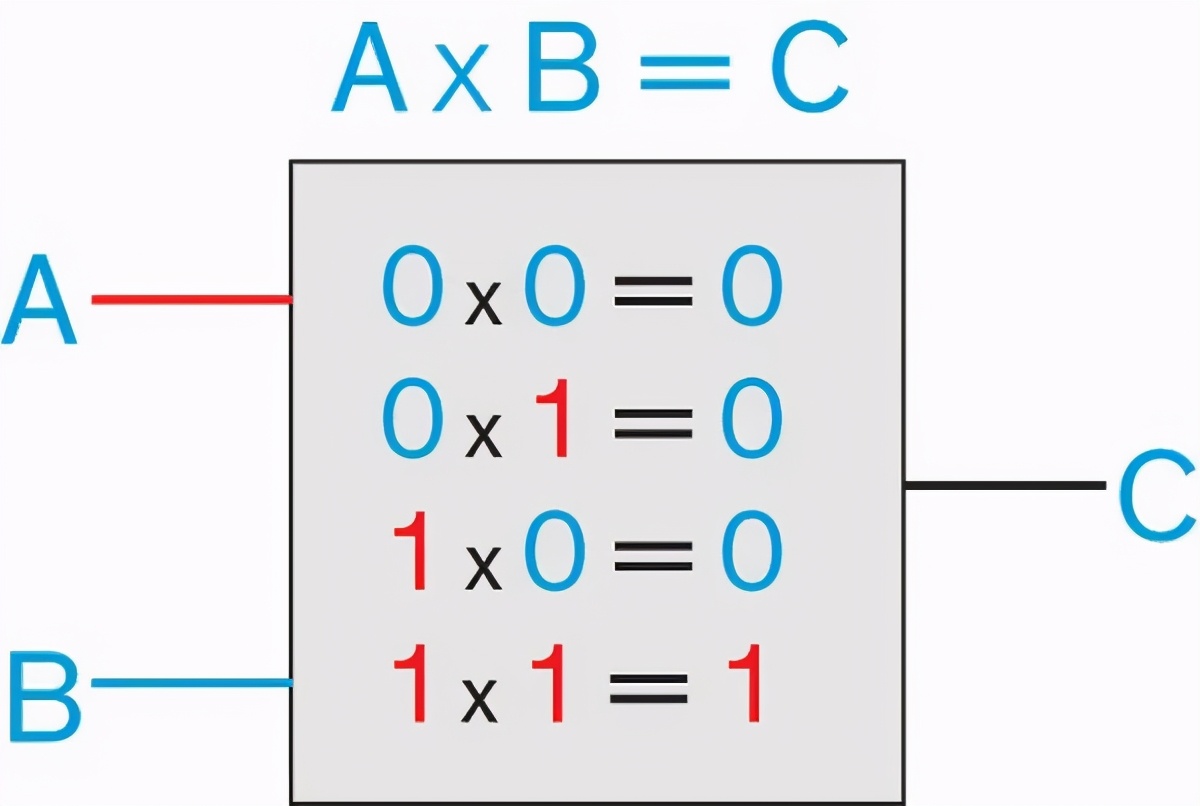
Sagredo:这和你们的反向电路区别在哪儿?
Salviati:我们用 p-bit 来构建电路,它既不是 0 也不是 1,而是在二者之间快速波动,一半的时间是 0,一半的时间是 1。
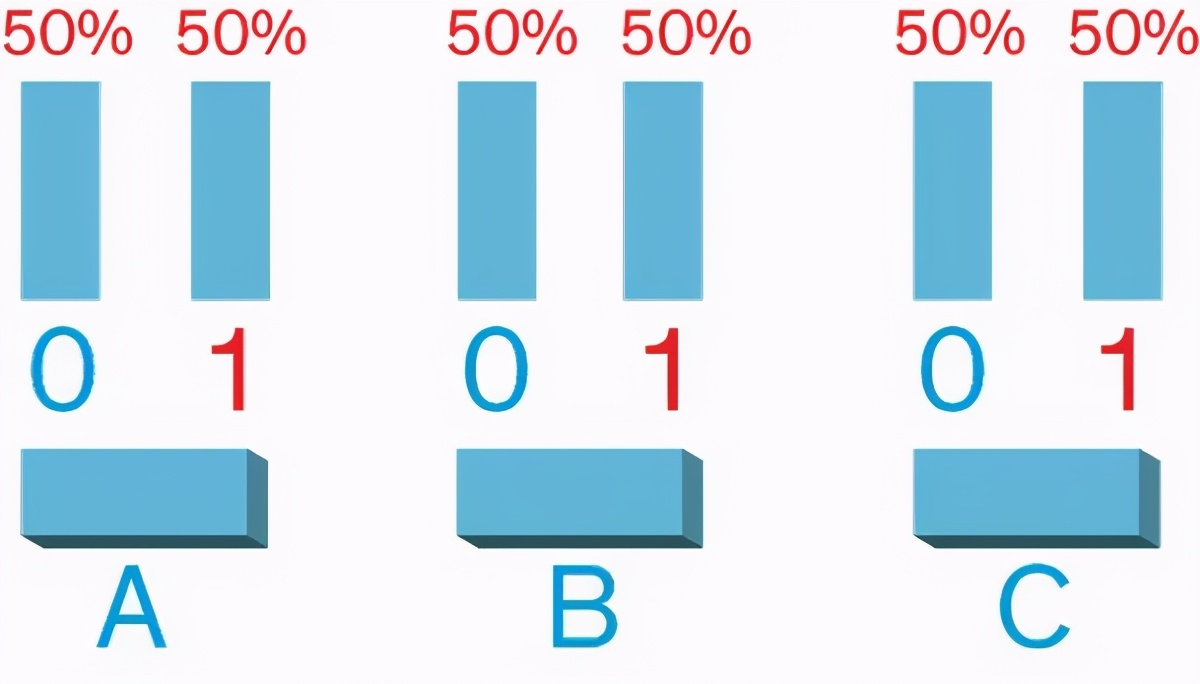
Sagredo:那这有什么用呢?这些比特根本不携带任何信息。
Salviati:没错,但如果我们让它们互相沟通,这些比特就有用了。你看,如果它们彼此之间不互相沟通,它们就会独立地在 0 和 1 之间波动。我们可以画一个像这样的直方图来表示 A、B 和 C 所有组合的概率。八种可能性中的每一种都是等可能的。
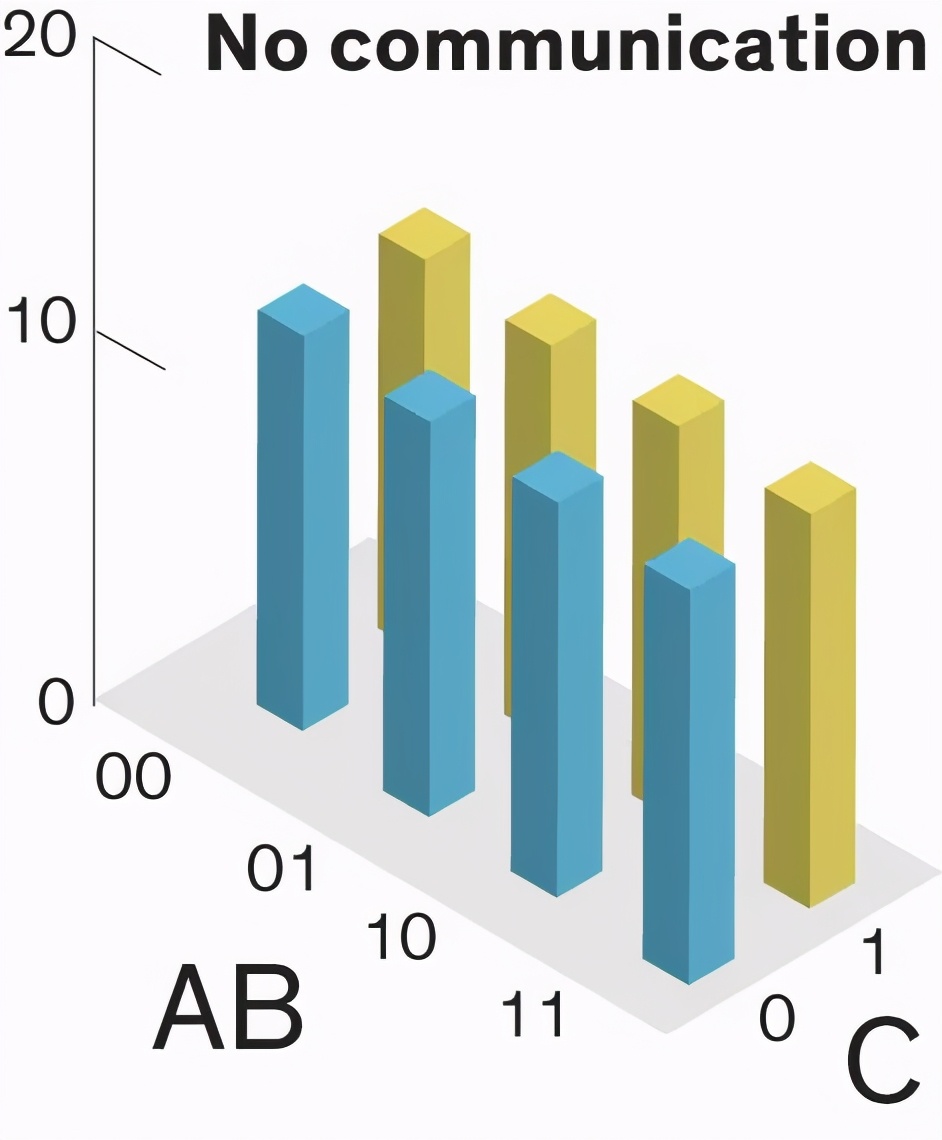
Salviati:现在假设 A、B 和 C 可以互相沟通,而且它们喜欢相互倾听和模仿。那么如果 A 变成 1,B 和 C 也会变成 1。如果 A 变成 0,B 和 C 也会相继变成 0。现在再画一个直方图,我们可以看到峰值只剩下两个。
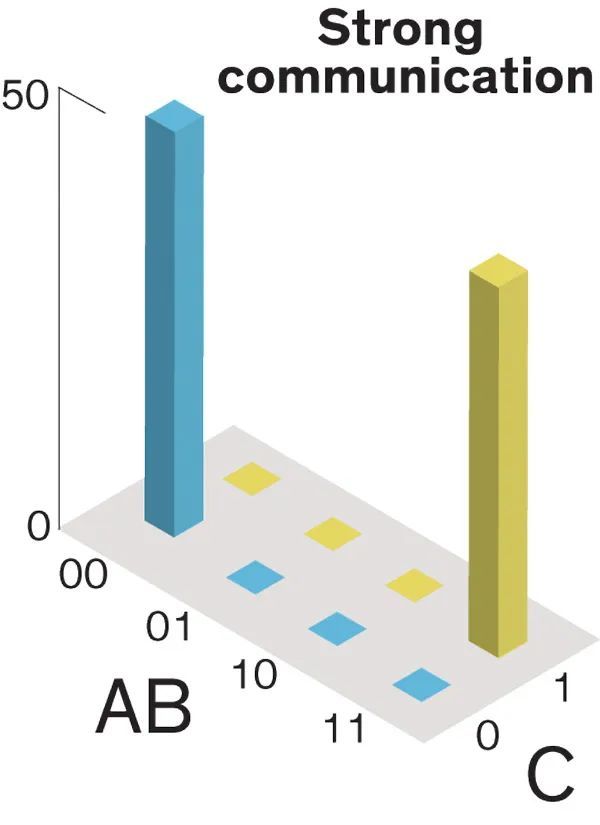
此时,我们的 p-bit 小磁体仍旧保持波动,但它们的波动是一致的。
Sagredo:就好像你有了一个在 0 和 1 之间波动的大磁体,但这个大磁铁看起来也没多大用。
Salviati:确实如此。如果我们有一个非常积极的沟通,就能得到一个大磁体。为了使这一点有用,我们必须巧妙地设计它们之间的通信,以便出现所需的一组峰值。
举个例子,如果我们想实现 1 比特乘法器,我们只需要 8 个峰值中的 4 个出现。对于 ,我们想要看到的是:, , , 。
如果能通过精心设计 p-bit 之间的通信来实现这一点,我们就得到了前面提到的可逆电路。
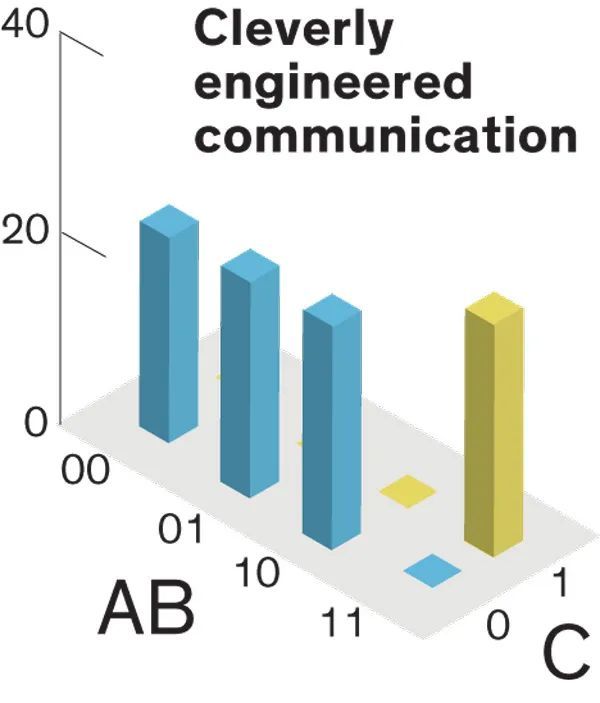
Sagredo:这是怎么做到的?
Salviati:让三个磁体在四种可能之间自由穿梭:, , , 。
但如果我们强制地将 A 和 B 磁体锁定为 0,那么这些磁体就只剩下了一种选择:,也就是说,C 只能为 0。
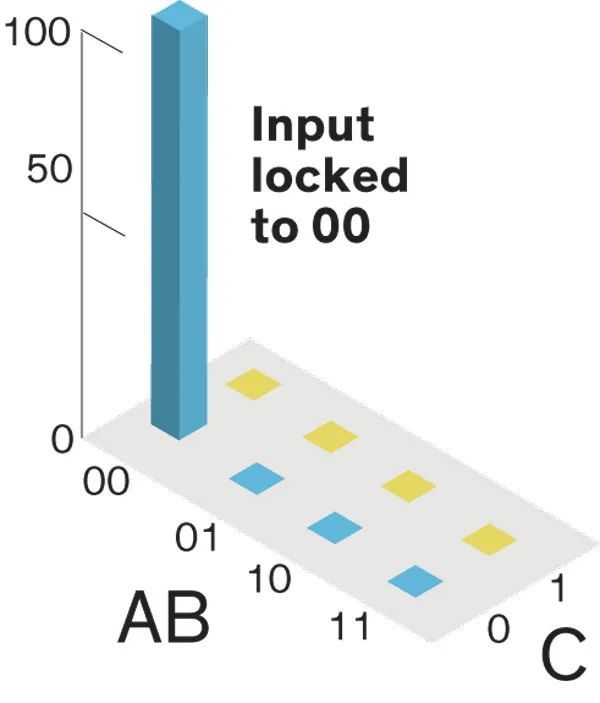
Sagredo:这就像一个以正向模式运行的乘法器:0 x 0 = 0,对不对?
Salviati:是的。如果要以反向模式运行,我们可以将 C 锁定为 0。如此一来,该系统将在以下三个选项之间波动:, , 。这是反向的乘法器。给定输出 0,系统告诉我们有三种可能的输入与之对应,分别是:0 x 0, 0 x 1, 和 1 x 0。
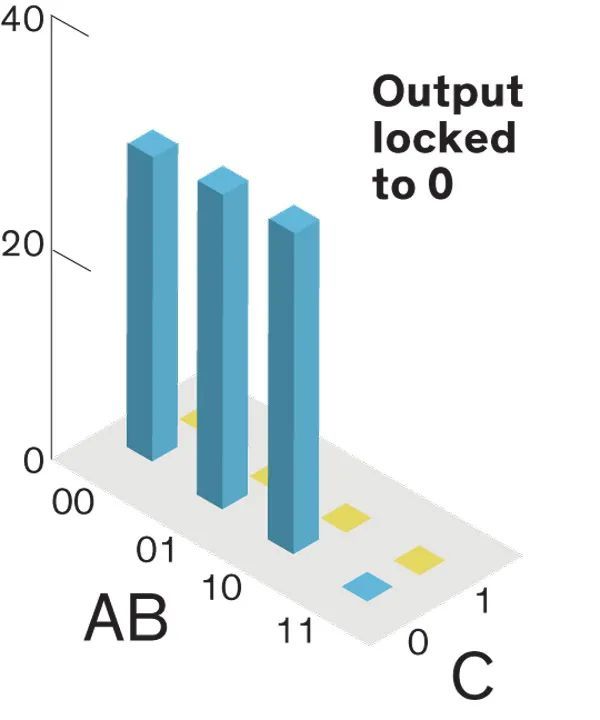
Sagredo:我明白了。但是你如何在你的 p-bit 之间设计这种神奇的通信呢?换句话说,你怎么知道要设计什么样的通信方式?
Salviati:有一些成熟的方法可以用来确定创建一组所需的峰值需要何种通信方式。
Sagredo:你这是在闪烁其词。根据你前面的说法,我还以为这是你们自己想出来的,所以才那么兴奋。
Salviati:事实上,这部分是众所周知的,至少对某些应用是这样。一些公司正在使用普通硬件和随机数生成器来构建概率计算机,以模拟我刚才说的概率位翻转。但这样做会浪费很多能量,很快就能把笔记本电脑的电池耗尽。我们的电路只需要三个晶体管和一个特殊的硬件元件就能实现同样的功能,这个硬件元件的内在物理特性产生了随机数。
Sagredo:能否介绍一下这个特殊元件?
Salviati:我们使用了一种名为磁穿隧接面(magnetic tunnel junction)的东西来建造一个简洁的装置,该装置可以让 p-bit 沟通起来非常容易。我们设它的输出为 V_out,这个输出是波动的。如果 V_in 为 0,V_out 就会有 50% 的时间为 1,50% 的时间为 0。但如果 V_in 是正的,V_out 就更有可能是 0。如果 V_in 是负的,V_out 就更有可能是 1。如果你让 V_in 一直是正的或负的,你就可以将输出「锁定」为某个状态。
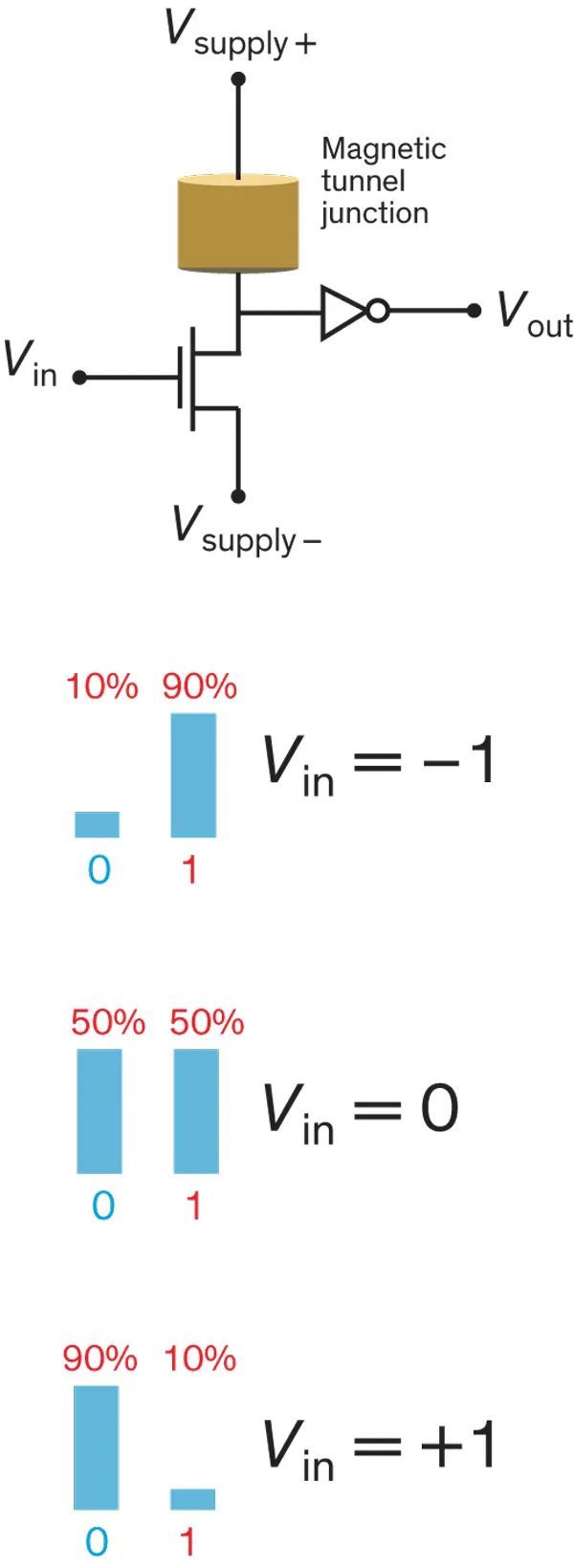
这就是每个 p-bit 通过输入电压 V_in 倾听其他 p-bit 的方式,它通过输出电压 Vout 来「说话」。比如,p-bit A 可以通过将 A 的输出反馈给 B 的输入来与 p-bit B 通信。我们用这个装置构造了可逆电路。到目前为止,我们还没有做什么惊天动地的事情:它们只是一个概念性的证明。但我们已经表明,这样的设备可以用先进的技术构造出来。有朝一日,我们可以利用这样的技术构造出巨大的电路,以解决现实世界的问题。
Sagredo:现实世界的问题是指哪些问题?
Salviati:比如优化问题,在这类问题中,你需要找到使某个成本函数最小化的配置。
人们每天都在解决优化问题,比如找到递送一堆包裹的最佳顺序,使得快递员走的距离最短。类似的问题可以映射到我们使用的基本架构上。每个问题都需要特定的连接模式。一旦我们弄清楚这些模式并把它正确地连接起来,p-bit 电路就能以配置峰值的形式给出答案。
Sagredo:Okay,你激发了我对这个系统的兴趣。但我们马上就要着陆了,还有什么渠道能让我了解你们的研究吗?
Salviati:我们最近发表了一篇文章,介绍了如何构造一台能够计算亲属之间遗传亲缘程度的 p-bit 计算机,你可以看一下。

文章链接:
https://spectrum.ieee.org/computing/hardware/waiting-for-quantum-computing-try-probabilistic-computing
两年过去,研究者取得了哪些新进展
自 2019 年展示用于概率计算机的硬件以来,普渡大学等机构的研究团队还利用现有的硅技术,通过 Amazon Web Services 公开提供的传统硬件模拟了一台具有数千个 p-bit 的概率计算机(相关链接:
https://ieeexplore.ieee.org/abstract/document/9173656)。
此外,研究者还发表了几篇关于集成单个硬件组件的进展的论文,试图建模更大的系统,并从一开始就确保能源效率(相关链接:
https://onlinelibrary.wiley.com/doi/abs/10.1002/adma.201906021)。
「关于 p-bit 的最佳实现目前还没有定论。但我们已经展示了哪些是有效的,确定最佳实现是迟早的事。」普渡大学的一位电子与计算机工程教授表示。
普渡大学的概率计算研究隶属于一个名为「Purdue-P」的项目。从名字来看,这些研究者似乎是唯一一批从事概率计算研究的学者,但在世界的其他地方,还有一些团队在用不同的材料和范式研究相似的技术。
普渡大学前博士后研究员 Kerem Camsari 表示,「作为一个领域,我们着眼于自身还不能解决的计算问题。同时我们也在想,现在有数字计算,有量子计算,还有什么?」「其实,从更高的层次来看,有很多东西都可以被称作『概率计算』」。































