提到回归算法,我想很多人都会想起线性回归,因为它通俗易懂且非常简单。但是,线性回归由于其基本功能和有限的移动自由度,通常不适用于现实世界的数据。
实际上,它只是经常用作评估和研究新方法时进行比较的基准模型。在现实场景中我们经常遇到回归预测问题,今天我就给大家总结分享 5 种回归算法。
1、神经网络回归
理论
神经网络的强大令人难以置信的,但它们通常用于分类。信号通过神经元层,并被概括为几个类。但是,通过更改最后的激活功能,它们可以非常快速地适应回归模型。
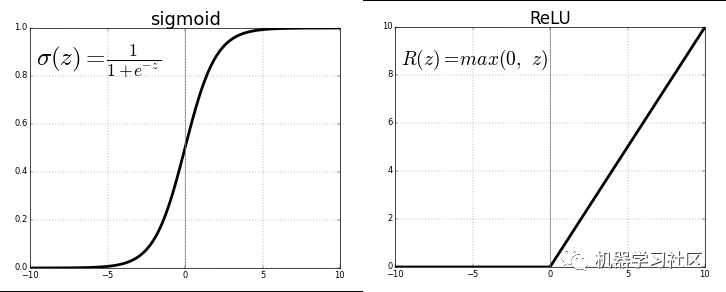
每个神经元通过激活功能传递以前连接的值,达到泛化和非线性的目的。常用的激活函数:Sigmoid 或 ReLU 函数。
通过将最后一个激活函数(输出神经元)替换为线性激活函数,可以将输出映射到固定类别之外的各种值。这样,输出不是将输入分类到任何一个类别中的可能性,而是神经网络将观测值置于其上的连续值。从这个意义上讲,它就像是线性回归的神经网络的补充。
神经网络回归具有非线性(除了复杂性)的优点,可以在神经网络中较早地通过S型和其他非线性激活函数引入神经网络。但是,由于 ReLU 忽略了负值之间的相对差异,因此过度使用 ReLU 作为激活函数可能意味着该模型倾向于避免输出负值。这可以通过限制 ReLU 的使用并添加更多的负值适当的激活函数来解决,也可以通过在训练之前将数据标准化为严格的正范围来解决。
实现
使用Keras,我们构建了以下人工神经网络结构,只要最后一层是具有线性激活层的密集层或简单地是线性激活层即可。
- model = Sequential()
- model.add(Dense(100, input_dim=3, activation='sigmoid'))
- model.add(ReLU(alpha=1.0))
- model.add(Dense(50, activation='sigmoid'))
- model.add(ReLU(alpha=1.0))
- model.add(Dense(25, activation='softmax'))
- #IMPORTANT PART
- model.add(Dense(1, activation='linear'))
神经网络的问题一直是其高方差和过度拟合的趋势。在上面的代码示例中,有许多非线性源,例如SoftMax或Sigmoid。如果你的神经网络在纯线性结构的训练数据上表现良好,则最好使用修剪后的决策树回归法,该方法可以模拟神经网络的线性和高变异性,但可以让数据科学家更好地控制深度、宽度和其他属性以控制过度拟合。
2、决策树回归
理论
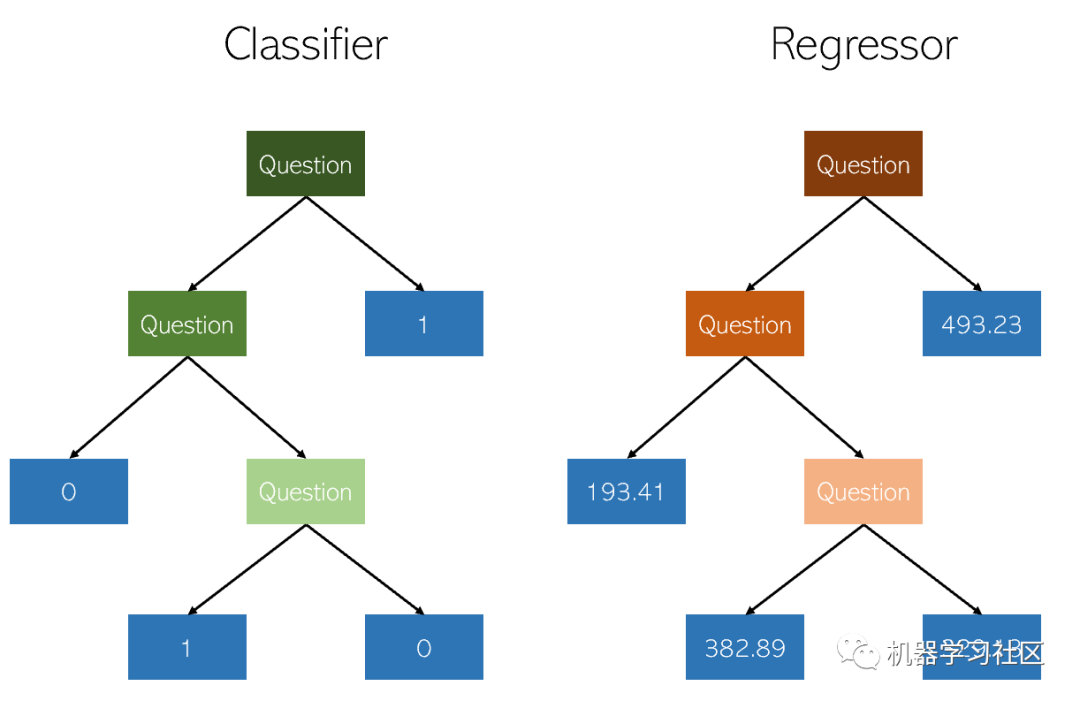
在决策树中分类和回归非常相似,因为两者都通过构造是/否节点的树来工作。虽然分类结束节点导致单个类值(例如,对于二进制分类问题为1或0),但是回归树以连续值(例如4593.49或10.98)结尾。
由于回归作为机器学习任务的特殊性和高差异性,因此需要仔细修剪决策树回归器。但是,它进行回归的方式是不规则的,而不是连续地计算值。因此,应该修剪决策树,使其具有最大的自由度。
实现
决策树回归可以很容易地在 sklearn 创建:
- from sklearn.tree import DecisionTreeRegressor
- model = DecisionTreeRegressor()
- model.fit(X_train, y_train)
由于决策树回归参数非常重要,因此建议使用sklearn的GridCV参数搜索优化工具来找到模型的正确准则。在正式评估性能时,请使用K折检验而不是标准的训练分割,以避免后者的随机性干扰高方差模型的精细结果。
3、LASSO 回归
理论
LASSO回归是线性回归的一种变体,特别适合于多重共线性(要素彼此之间具有很强的相关性)的数据。它可以自动执行部分模型选择,例如变量选择或参数消除。
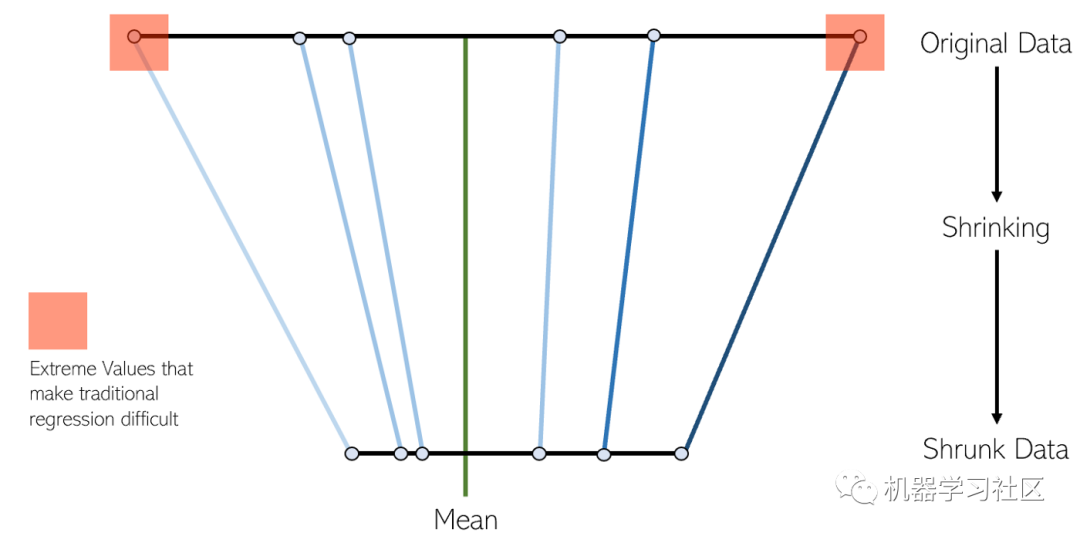
缩小的过程为回归模型增加了许多好处:
- 对真实参数的估计更加准确和稳定。
- 减少采样和非采样错误。
- 空间波动更平滑。
LASSO并没有像神经网络的高方差方法和决策树回归那样通过调整模型的复杂性来补偿数据的复杂性,而是试图通过变形空间来降低数据的复杂性,从而能够通过简单的回归技术来处理。在此过程中,LASSO自动以低方差方法帮助消除或扭曲高度相关和冗余的特征。
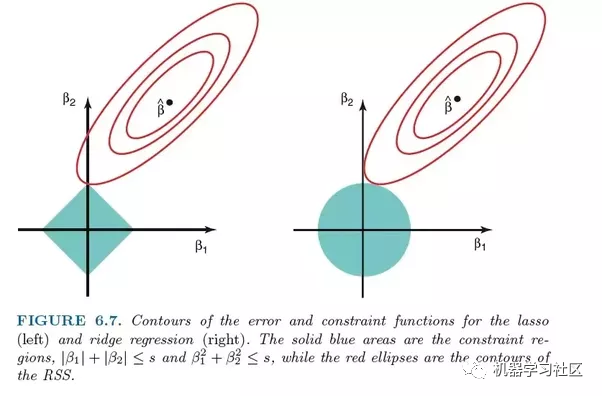
LASSO回归使用L1正则化,这意味着它按绝对值加权误差。这种正则化通常会导致具有较少系数的稀疏模型,这使得它具有可解释性。
实现
在sklearn中,LASSO回归附带了一个交叉验证模型,该模型可以选择许多具有不同基本参数和训练路径的训练模型中表现最佳的模型,从而使需要手动完成的任务实现自动化。
- from sklearn.linear_model import LassoCV
- model = LassoCV()
- model.fit(X_train, y_train)
4、Ridge回归
理论
Ridge回归与LASSO回归非常相似,因为它适用于收缩。Ridge和LASSO回归都非常适用于具有大量彼此不独立(共线性)的特征的数据集,但是两者之间最大的区别是Ridge利用L2正则化,由于L2正则化的性质,系数越来越接近零,但是无法达到零。
正因为如此,如果你希望对每个变量的优先级产生小的影响进行优先级排序,则 Ridge 是更好的选择。如果希望在模型中考虑几个变量,每个变量具有中等到较大的影响,则 LASSO 是更好的选择。
实现
Ridge回归可以在sklearn中实现,如下所示。像 LASSO 回归一样,sklearn可以实现交叉验证选择许多受过训练的模型中最好的模型的实现。
- from sklearn.linear_model import RidgeCV
- model = Ridge()
- model.fit(X_train, y_train)
5、ElasticNet 回归
理论
ElasticNet 试图通过结合L1和L2正则化来利用 Ridge 回归和 LASSOb回归中的最佳方法。
LASSO和Ridge提出了两种不同的正则化方法。λ是控制惩罚强度的转折因子。
- 如果λ= 0,则目标变得类似于简单线性回归,从而获得与简单线性回归相同的系数。
- 如果λ=∞,则由于系数平方的权重无限大,系数将为零。小于零的值会使目标无限。
- 如果0 <λ<∞,则λ的大小决定赋予物镜不同部分的权重。
除了λ参数之外,ElasticNet还添加了一个附加参数α,用于衡量L1和L2正则化应该如何"混合":
- 当α等于0时,该模型是纯粹的岭回归模型,
- 而当α等于1时,它是纯粹的LASSO回归模型。
“混合因子”α只是确定在损失函数中应考虑多少L1和L2正则化。
实现
可以使用 sklearn 的交叉验证模型来实现ElasticNet:
- from sklearn.linear_model import ElasticNetCV
- model = ElasticNetCV()
- model.fit(X_train, y_train)