计数排序虽然不是面试常考题目,但是计数排序的求统计数组步骤和最后元素归位思想是我们刷题时经常用到的,例如原地置换,使用数组模拟 hashmap 等,所以还是很有必要看一下的。
今天我们就一起来看看线性排序里的计数排序到底是怎么回事吧。
我们将镜头切到袁记菜馆
因为今年袁记菜馆的效益不错,所以袁厨就想给员工发些小福利,让小二根据员工工龄进行排序,但是菜馆共有 100000 名员工,菜馆开业 10 年,员工工龄从 0 - 10 不等。
看来这真是一个艰巨的任务啊。
当然我们可以借助之前说过的 归并排序 和 快速排序 解决,但是我们有没有其他更好的方法呢?
了解排序算法的老哥可能已经猜到今天写什么啦。是滴,我们今天来写写用空间换时间的线性排序。
说之前我们先来回顾一下之前的排序算法,最好的时间复杂度为 O(nlogn) ,且都基于元素之间的比较来进行排序。
我们来说一下非基于元素比较的排序算法,且时间复杂度为 O(n),时间复杂度是线性的,所以我们称其为线性排序算法。
其优势在于在对一定范围内的整数排序时,它的复杂度为Ο(n+k),此时的 k 则代表整数的范围。快于任何一种比较类排序算法,不过也是需要牺牲一些空间来换取时间。
下面我们先来看看什么是计数排序,这个计数的含义是什么?
我们假设某一分店共有 10 名员工,
工龄分别为 1,2,3,5,0,2,2,4,5,9
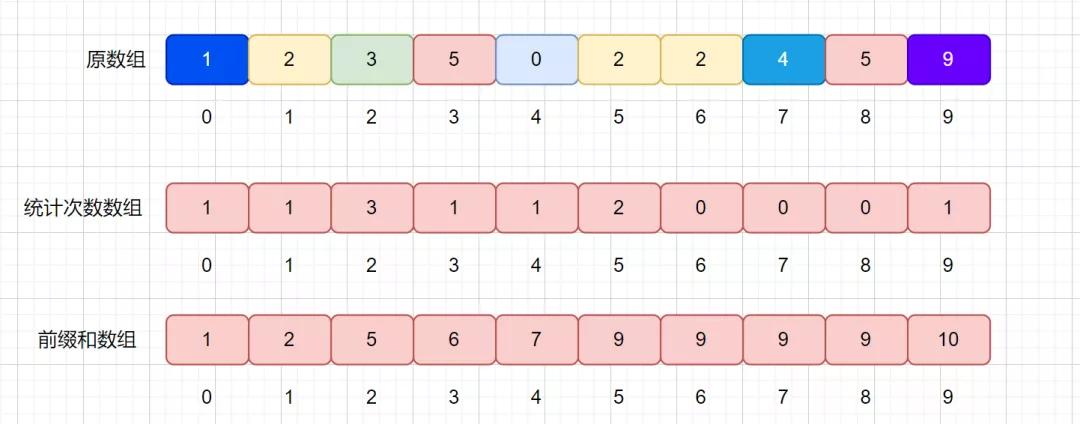
那么我们将其存在一个长度为 10 的数组里,,但是我们注意,我们数组此时存的并不是元素值,而是元素的个数。见下图
注:此时我们这里统计次数的数组长度根据最大值来决定,上面的例子中最大值为 9 ,则长度为 9 + 1 = 10。暂且先这样理解,后面会对其优化 。
我们继续以上图的例子来说明,在该数组中,索引代表的为元素值(也就是上面例子中的工龄),数组的值代表的则是元素个数(也就是不同工龄出现的次数)。
即工龄为 0 的员工有 1 个, 工龄为 1 的员工有 1 个,工龄为 2 的员工有 3 个 。。。
然后我们根据出现次数将其依次取出看看是什么效果。
0,1,2,2,2,3,4,5,5,9
我们发现此时元素则变成了有序的,但是这并不是排序,只是简单的按照统计数组的下标,输出了元素值,并没有真正的给原始数组进行排序。
这样操作之后我们不知道工龄属于哪个员工。
见下图
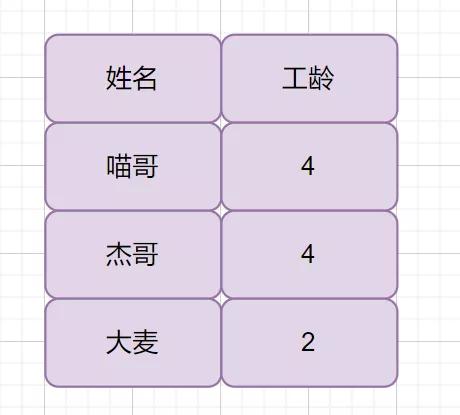
举例
虽然喵哥和杰哥工龄相同,如果我们按照上面的操作输出之后,我们不能知道工龄为 4 的两个员工,哪个是喵哥哪个是杰哥。
所以我们需要借助其他方法来对元素进行排序。
大家还记不记得我们之前说过的前缀和,下面我们通过上面统计次数的数组求出其前缀和数组。
因为我们是通过统计次数的数组得到了前缀和数组,那么我们来分析一下 presum 数组里面值的含义。
例如我们的 presum[2] = 5 ,代表的则是原数组小于等于 2 的值共有 5 个。presum[4] = 7 代表小于等于 4 的元素共有 7 个。
是不是感觉计数排序的含义要慢慢显现出来啦。
其实到这里我们已经可以理解的差不多了,还差最后一步,
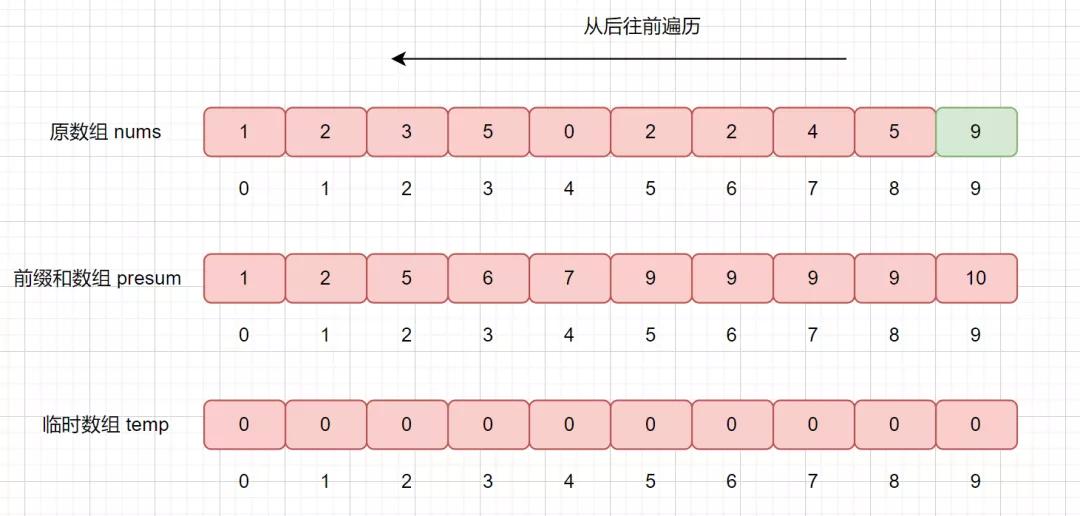
此时我们要从后往前遍历原始数组,然后将遍历到的元素放到临时数组的合适位置,并修改 presum 数组的值,遍历结束后则达到了排序的目的。
这时有人要问了,为什么我们要从后往前遍历呢?
这个问题的答案,我们等下说,继续往下看吧。
计数排序
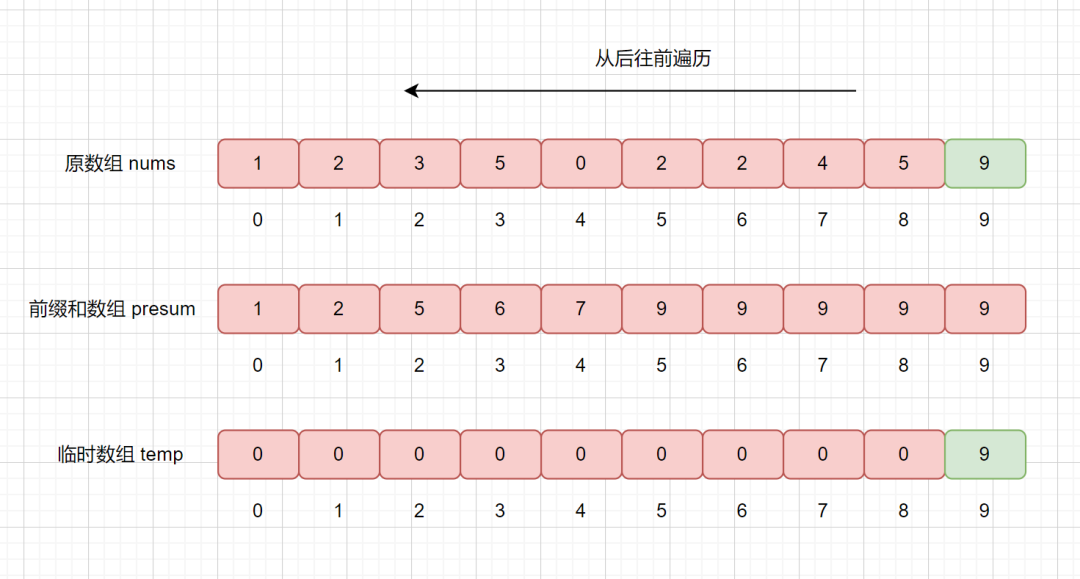
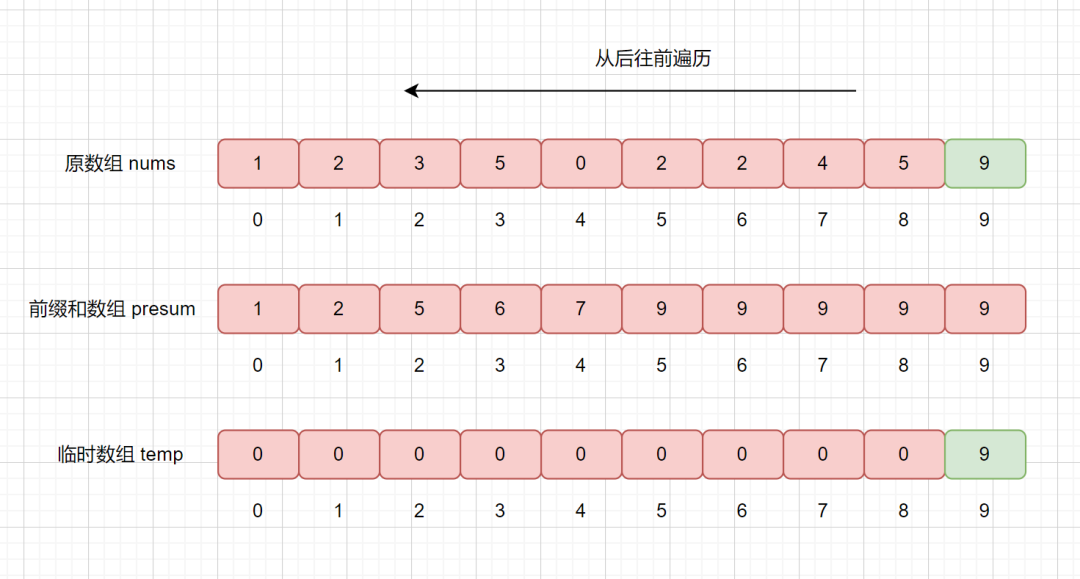
我们从后往前遍历,nums[9] = 9,则我们拿该值去 presum 数组中查找,发现 presum[nums[9]] = presum[9] = 10 ,
大家还记得我们 presum 数组里面每个值的含义吗,我们此时 presum[9] = 10,则代表在数组中,小于等于的数共有 10 个,则我们要将他排在临时数组的第 10 个位置,也就是 temp[9] = 9。
我们还需要干什么呢?我们想一下,我们已经把 9 放入到 temp 数组里了,已经对其排好序了,那么我们的 presum 数组则不应该再统计他了,则将相应的位置减 1 即可,也就是 presum[9] = 10 - 1 = 9;
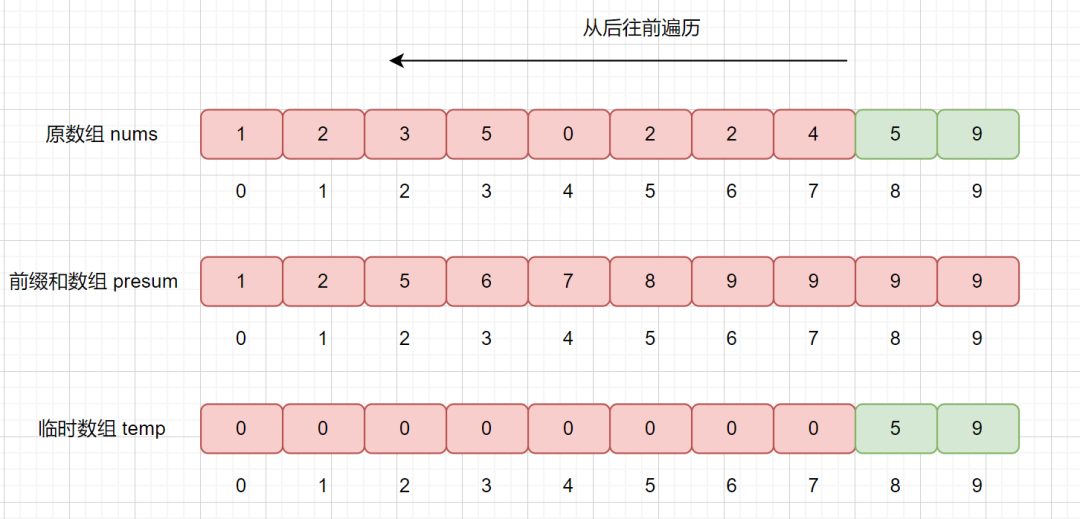
下面我们继续遍历 5 ,然后同样执行上诉步骤
我们继续查询 presum 数组,发现 presum[5] = 9,则说明小于等于 5 的数共有 9 个,我们将其放入到 temp 数组的第 9 个位置,也就是
temp[8] = 5。然后再将 presum[5] 减 1 。
是不是到这里就理解了计数排序的大致思路啦。
那么我们为什么需要从后往前遍历呢?我们思考一下,如果我们从前往后遍历,相同元素的话,前面的元素则会先归位再减一,这样则会使计数排序变成不稳定的排序算法。
这个排序的过程像不像查字典呢?通过查询 presum 数组,得出自己应该排在临时数组的第几位。然后再修改下字典,直到遍历结束。
那么我们先来用动画模拟一下我们这个 bug 版的计数排序,加深理解。
注:我们得到 presum 数组的过程在动画中省略。直接模拟排序过程。
但是到现在就完了吗?显然没有,我们思考下这个情况。
假如我们的数字为 90,93,94,91,92 如果我们根据上面方法设置 presum 数组的长度,那我们则需要设置数组长度为 95(因为最大值是94),这样显然是不合理的,会浪费掉很多空间。
还有就是当我们需要对负数进行排序时同样会出现问题,因为我们求次数的时候是根据 nums[index] 的值来填充 presum 数组的,所以当 nums[index] 为负数时,填充 presum 数组时则会报错。
此时通过最大值来定义数组长度也不合理。
所以我们需要采取别的方法来定义数组长度。
下面我们来说一下偏移量的概念。
例如 90,93,94,91,92,我们 可以通过 max ,min 的值来设置数组长度即 94 - 90 + 1 = 5 。偏移量则为 min 值,也就是 90。那么我们的 90 则对应索引 0 。
见下图。
这样我们填充 presum 数组时就不会出现浪费空间的情况了,负数?出现负数的情况当然也可以。继续看
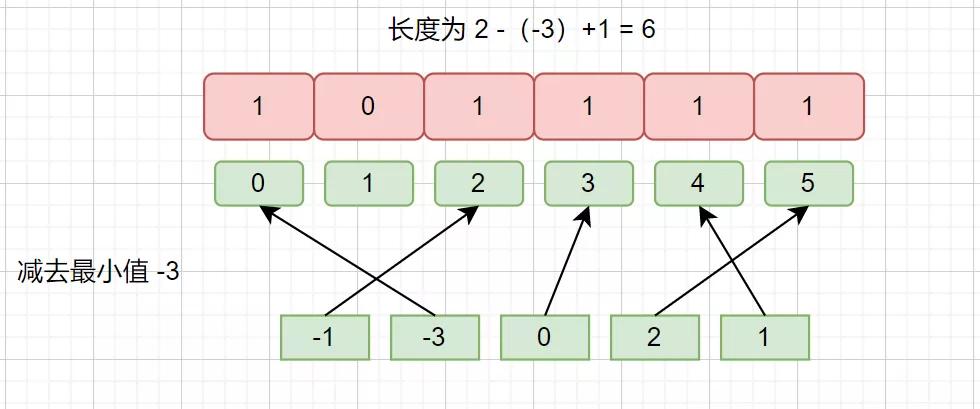
例如:-1,-3,0,2,1
一样可以,哦了,到这里我们就搞定了计数排序,下面我们来看一哈代码吧。
- class Solution {
- public int[] sortArray(int[] nums) {
- int len = nums.length;
- if (nums.length < 1) {
- return nums;
- }
- //求出最大最小值
- int max = nums[0];
- int min = nums[0];
- for (int x : nums) {
- if (max < x) max = x;
- if (min > x) min = x;
- }
- //设置 presum 数组长度,然后求出我们的前缀和数组,
- //这里我们可以把求次数数组和前缀和数组用一个数组处理
- int[] presum = new int[max-min+1];
- for (int x : nums) {
- presum[x-min]++;
- }
- for (int i = 1; i < presum.length; ++i) {
- presum[i] = presum[i-1]+presum[i];
- }
- //临时数组
- int[] temp = new int[len];
- //遍历数组,开始排序,注意偏移量
- for (int i = len-1; i >= 0; --i) {
- //查找 presum 字典,然后将其放到临时数组,注意偏移度
- int index = presum[nums[i]-min]-1;
- temp[index] = nums[i];
- //相应位置减一
- presum[nums[i]-min]--;
- }
- //copy回原数组
- System.arraycopy(temp,0,nums,0,len);
- return nums;
- }
- }
好啦,这个排序算法我们已经搞定了,下面我们来扒一扒它。
计数排序时间复杂度分析
我们的总体运算量为 n+n+k+n ,总体运算是 3n + k 所以时间复杂度为 O(N+K);
计数排序空间复杂度分析
我们用到了辅助数组,空间复杂度为 O(n)
计数排序稳定性分析
稳定性在我们最后存入临时数组时有体现,我们当时让其放入临时数组的合适位置,并减一,所以某元素前面的相同元素,在临时数组,仍然在其前面。所以计数排序是稳定的排序算法。
虽然计数排序效率不错但是用到的并不多。
- 这是因为其当数组元素的范围太大时,并不适合计数排序,不仅浪费时间,效率还会大大降低。
- 当待排序的元素非整数时,也不适用,大家思考一下这是为什么呢?
好啦,今天的文章就到这啦,我们下期再见,拜了个拜