0. 提要钩玄
前面在文章【数据结构之链表】看完这篇文章我终于搞懂链表了中已经介绍了链式存储结构,介绍了链式存储结构的最基本(简单)实现——单向链表。
单向链表,顾名思义,它是单向的。
因为单链表的每个结点只有一个数据域和一个指针域,而该指针域只存储了下一个结点的地址,所以我们只能通过某结点找到其直接后继结点,却不能通过某节点找到其直接前驱结点。
此外,由于单链表到尾结点(链表的最后一个结点)结束,所以尾结点的指针域是 NULL,以此来表示链表的终止,这就导致我们遍历到尾结点的时候,如果想再次遍历,只能手动回到头结点再开始遍历。
为了弥补单链表的上面两个缺点,下面介绍两种链表,它们都是单链表的变形,如果你理解了单链表,那么会很容易理解这两种变形。
目录
1. 单向循环链表
1.1. 结构
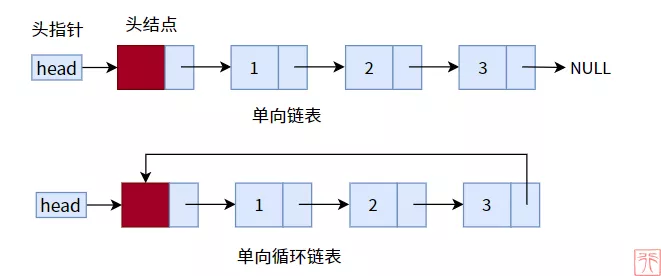
单链表的尾结点的指针域是 NULL,所以单链表到此终止。如果我们使用单链表的尾结点的指针域存储头结点的地址,即尾结点的直接后继结点为头结点,如此一来,单链表就构成了一个环(循环),称之为单项循环链表。
1.2. 实现思路
单向循环链表是由单链表进化而来的,算是单链表的“儿子”,所以单链表的那一套结构对于单向循环链表来说完全适用,从上图你也可以看出,结构并无较大改变,二者所不同只在尾结点,所以我们只需要在尾结点和与尾结点相关的操作上下功夫就行了。
因此,单向循环链表的结构体和单链表的结构体相同。
- /*单向循环链表的结点的结构体*/
- typedef struct _Node {
- int data; //数据域:存储数据
- struct _Node *next; //指针域:存储直接后继结点的地址
- } Node;
为了统一对空链表和非空链表的操作,我们使用带头结点的链表来实现它。
1.3. 空链表及初始化
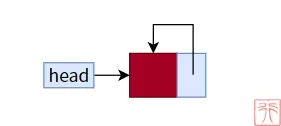
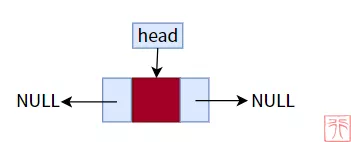
一个空链表如图所示,只有一个头指针和头结点:
空链表
头结点的指针域指向其本身构成一个循环,我们可以借此来判断链表是否为空。
- if (head->next == head) {
- printf("空链表。\n");
- }
想要初始化一个空链表很简单,创造头结点,使头结点的 next 指针指向其自身即可:
- Node *create_node(int elem)
- {
- Node *new = (Node *) malloc(sizeof(Node));
- new->data = elem;
- new->next = NULL;
- return new;
- }
- /**
- * 初始化链表
- * p_head: 指向头指针的指针
- */
- void init(Node **p_head)
- {
- //创建头结点
- Node *head_node = create_node(0);
- //头指针指向头结点
- *p_head = head_node;
- //头结点的next指针指向其本身,构成环
- head_node->next = head_node;
- }
1.4. 插入操作
这里只演示头插法和尾插法
【头插法】
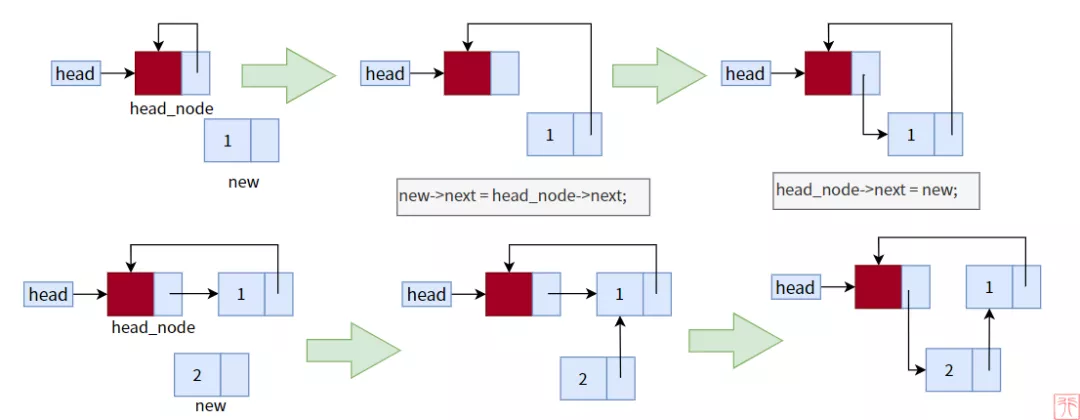
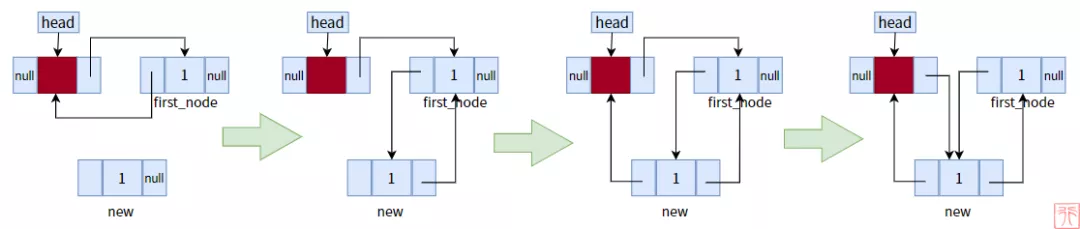
因为带头结点,所以不需要考虑是否为空链表。下图是向空链表中头插两个元素的过程:
单向循环链表头插法过程
- /**
- * 头插法,新结点为头结点的直接后继
- * p_head: 指向头指针的指针
- * elem: 新结点的数据
- */
- void insert_at_head(Node **p_head, int elem)
- {
- Node *new = create_node(elem);
- Node *head_node = *p_head; //头结点
- //新结点插入头结点之后
- new->next = head_node->next;
- head_node->next = new;
- }
【尾插法】
因为为了尽量简单,所以我们并没有设置指向尾结点的尾指针,所以在尾插之前,需要先借助某个指针,遍历至尾结点,然后再插入。
- /**
- * 尾插法:新插入的结点始终在链表尾
- * p_head: 指向头指针的指针
- * elem: 新结点的数据
- */
- void insert_at_tail(Node **p_head, int elem)
- {
- Node *new = create_node(elem);
- Node *head_node = *p_head; //头结点
- Node *tail = head_node; //tail指针指向头结点
- while (tail->next != head_node) { //tail遍历至链表尾
- tail = tail->next;
- }
- //尾插
- new->next = tail->next;
- tail->next = new;
- }
1.5. 删除操作
删除的本质是“跳过”待删除的结点,所以我们要找到待删除结点的直接前驱结点,然后让其直接前驱结点的 next 指针指向其直接后继结点,以此来“跳过”待删除结点,最后保存其数据域,释放结点,即完成删除。
这里只演示头删法。
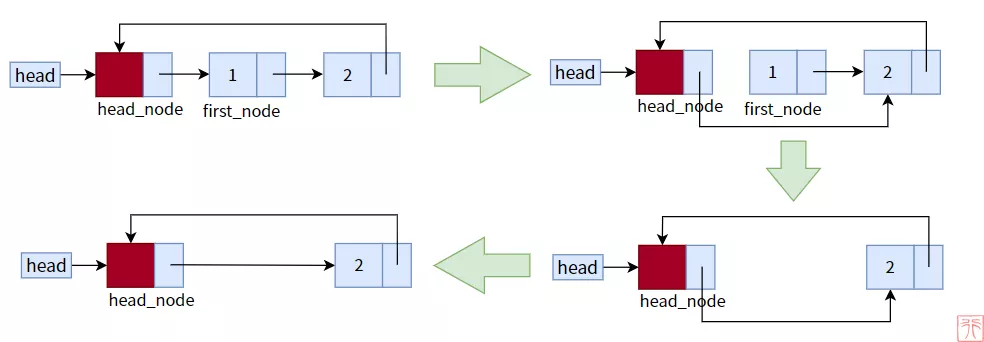
因为删除的是头结点的直接后继结点,所以我们不必再费力寻找待删除结点的直接前驱结点了。
单向循环链表头删法过程
- /**
- * 头删法:删除头结点之后的结点
- * p_head: 指向头指针的指针
- * elem: 指向保存数据变量的指针
- */
- void delete_from_head(Node **p_head, int *elem)
- {
- Node *head_node = *p_head; //头结点
- if (head_node->next == head_node) {
- printf("空链表,无元素可删。\n");
- return;
- }
- Node *first_node = head_node->next; //首结点:头结点的下一个结点
- *elem = first_node->data; //保存被删除结点的数据
- head_node->next = first_node->next; //删除结点
- free(first_node); //释放
- }
1.6. 遍历操作
我们可以一圈又一圈地循环遍历链表,下面是循环打印 20 次结点地代码:
- /**
- * 循环打印20次结点
- */
- void output_20(Node *head)
- {
- if (head->next == head) {
- printf("空链表。\n");
- return;
- }
- Node *p = head->next;
- for (int i = 0; i <= 20; i++) {
- if (p != head) { //不打印头结点
- printf("%d ", p->data);
- }
- p = p->next;
- }
- printf("\n");
- }
2. 双向链表
2.1. 结构
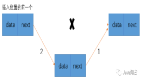
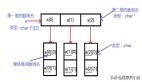
顾名思义,双向链表,就是有两个方向,一个指向前,一个指向后。这样我们就弥补了单链表的某个结点只能找到其直接后继的缺陷。如图所示:
双向链表
2.2. 实现思路
为了实现能指前和指后的效果,只靠 next 指针肯定是不够的,所以我们需要再添加一个指针 —— prev,该指针指向某结点的直接前驱结点。
- /*双向链表的结点结构体*/
- typedef struct _Node {
- int data; //数据域
- struct _Node *prev; //指向直接前驱结点的指针
- struct _Node *next; //指向直接后继结点的指针
- } Node;
2.3. 空链表及初始化
双向链表的空链表如图所示:
要初始化一个这样的空链表,需要创造出头结点,然后将两个指针域置空即可:
- Node *create_node(int elem)
- {
- Node *new = (Node *)malloc(sizeof(Node));
- new->data = elem;
- new->prev = NULL;
- new->next = NULL;
- return new;
- }
- void init(Node **p_head)
- {
- //创建头结点
- Node *head_node = create_node(0);
- //头指针指向头结点
- *p_head = head_node;
- }
2.4. 插入操作
这里只演示头插法,过程如下:
双向链表头插法过程
代码如下:
- /**
- * 头插法,新结点为头结点的直接后继
- * p_head: 指向头指针的指针
- * elem: 新结点的数据
- */
- void insert_at_head(Node **p_head, int elem)
- {
- Node *new = create_node(elem);
- Node *head_node = *p_head; //头结点
- if (head_node->next != NULL) { //不为空链表
- Node *first_node = head_node->next; //首结点:头结点的下一个结点
- //首结点的prev指针指向new结点
- first_node->prev = new;
- //new结点的next指针指向首结点
- new->next = first_node;
- }
- //new结点的prev指针指向头结点
- new->prev = head_node;
- //头结点的next指针指向new结点
- head_node->next = new;
- }
2.5. 删除操作
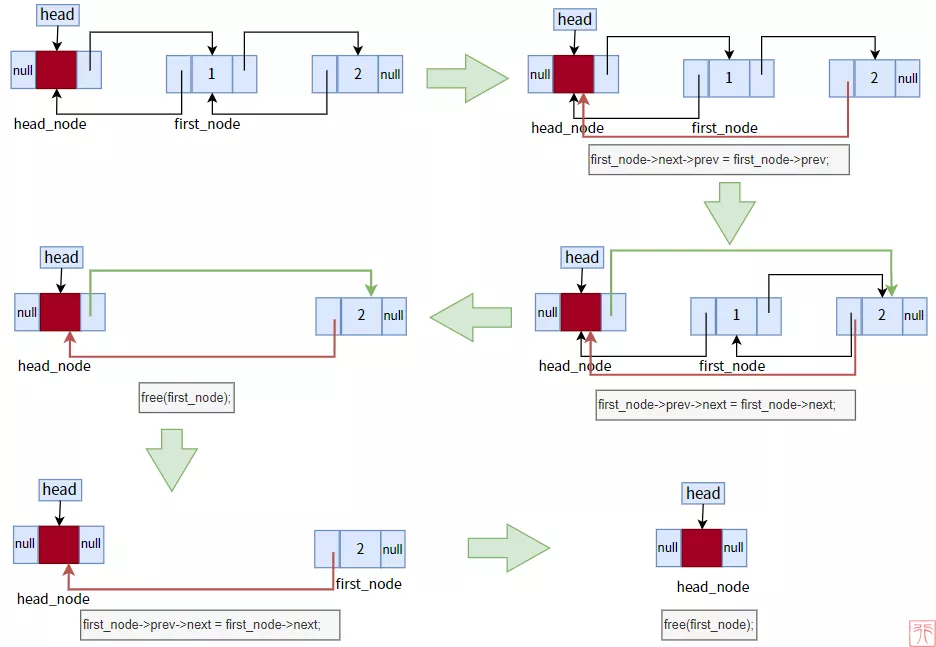
这里只演示头删法。下图是将一个有两个元素结点的双向链表头删为空链表的过程:
双向链表头删法过程
代码如下:
- /**
- * 头删法
- * p_head: 指向头指针的指针
- * elem: 指向保存变量的指针
- */
- void delete_from_head(Node **p_head, int *elem)
- {
- Node *head_node = *p_head; //头结点
- Node *first_node = head_node->next; //待删除的首结点:头结点的下一个结点
- if (head_node->next == NULL) { //判空
- printf("空链表,无元素可删。\n");
- return;
- }
- *elem = first_node->data; //保存数据
- if (first_node->next != NULL) {
- first_node->next->prev = first_node->prev;
- }
- first_node->prev->next = first_node->next;
- free(first_node);
- }
2.6. 遍历操作
有了 next 指针域,我们可以一路向后遍历;有了 prev 指针域,我们可以一路向前遍历。
这里不再展示代码了。
3. 总结
了解了单向循环链表和双向链表,就像拿搭积木一样,我们还可以创造出来双向循环链表。这里就不再演示了,读者可以自行尝试。只要你搞懂上面三种链表,这绝非难事。
以上就是链表的花样玩法部分内容,以后还会继续更新。
参考资料
[1]GitHub: https://github.com/xingrenguanxue/Simple-DS-and-Easy-Algo
[2]Gitee: https://gitee.com/xingrenguanxue/Simple-DS-and-Easy-Algo