Python时间序列异常检测ADTK

[[390668]]

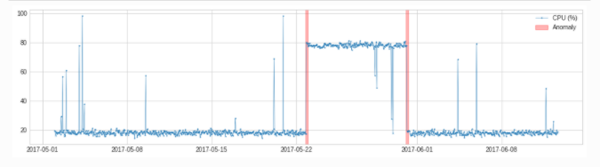
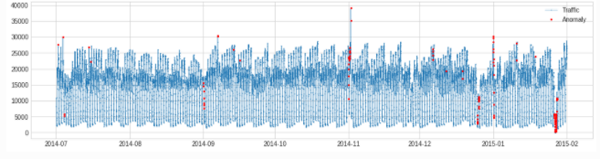
 1. adtk简介

智能运维AIOps的数据基本上都是时间序列形式的，而异常检测告警是AIOps中重要组成部分。笔者最近在处理时间序列数据时有使用到adtk这个python库，在这里和大家做下分享。

什么是adtk?

adtk（Anomaly Detection Toolkit）是无监督异常检测的python工具包，它提供常用算法和处理函数：

•  简单有效的异常检测算法（detector）
•  异常特征加工（transformers）
•  处理流程控制（Pipe）

2. 安装

pip install adtk 

3. adtk数据要求

时间序列的数据主要包括时间和相应的指标（如cpu，内存，数量等）。python中数据分析一般都是pandas的DataFrame，adtk要求输入数据的索引必须是DatetimeIndex。

pandas提供了时间序列的时间生成和处理方法。

•  pd.date_range 

stamps = pd.date_range("2012-10-08 18:15:05", periods=4, freq="D")  
# DatetimeIndex(['2012-10-08 18:15:05', '2012-10-09 18:15:05',  
#           '2012-10-10 18:15:05', '2012-10-11 18:15:05'],  
#          dtype='datetime64[ns]', freq='D') 

•  pd.Timestamp 

tmp = pd.Timestamp("2018-01-05") + pd.Timedelta("1 day")  
 print(tmp, tmp.timestamp(), tmp.strftime('%Y-%m-%d'))  
 # 2018-01-06 00:00:00 1515196800.0 2018-01-06  
 pd.Timestamp( tmp.timestamp(), unit='s', tz='Asia/Shanghai')  
 # Timestamp('2018-01-06 08:00:00+0800', tz='Asia/Shanghai') 

•  pd.to_datetime

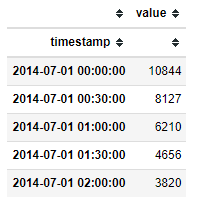
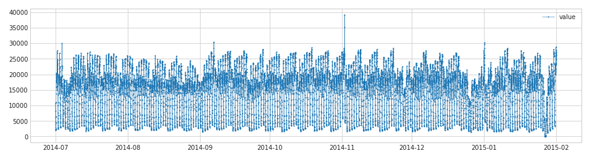
adtk提供是validate_series来验证时间序列数据的有效性，如是否按时间顺序 

import pandas as pd  
from adtk.data import validate_series  
from adtk.visualization import plot  
df = pd.read_csv('./data/nyc_taxi.csv', index_col="timestamp", parse_dates=True)  
df = validate_series(df)  
plot(df) 

4. 异常特征加工（transformers）

adtk中transformers提供了许多时间序列特征加工的方法：

•  一般我们获取时间序列的特征，通常会按照时间窗口在滑动，采集时间窗口上的统计特征；
•  还有对于季节性趋势做分解，区分哪些是季节性的部分，哪些是趋势的部分
•  时间序列降维映射：对于细粒度的时间序列数据，数据量大，对于检测算法来说效率不高。降维方法能保留时间序列的主要趋势等特征同时，降低维数，提供时间效率。这个对于用CNN的方式来进行时间序列分类特别有效，adtk主要提供基于pca的降维和重构方法,主要应用于多维时间序列。

4.1 滑动窗口

atdk提供单个宽口RollingAggregate和2个窗口DoubleRollingAggregate的滑动方式。统计特征支持均值，中位数，汇总，最大值，最小值，分位数， 方差，标准差，偏度，峰度，直方图 等，['mean', 'median', 'sum', 'min', 'max', 'quantile', 'iqr', 'idr', 'count', 'nnz', 'nunique', 'std', 'var', 'skew', 'kurt', 'hist']其中

•  'iqr': 是分位数 75% 和 25%差值
•  'idr': 是分位数 90% 和 10%插值
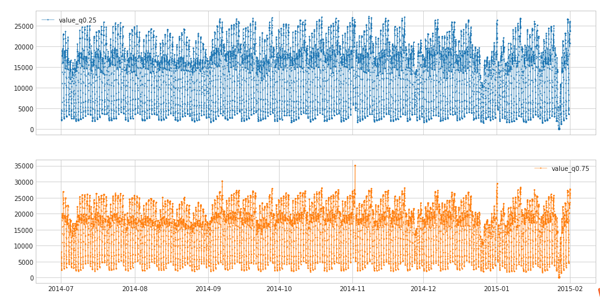
•   RollingAggregate 

import pandas as pd  
  from adtk.data import validate_series  
  from adtk.transformer import RollingAggregate  
  from adtk.transformer import DoubleRollingAggregate  
  s = pd.read_csv('./data/nyc_taxi.csv', index_col="timestamp", parse_dates=True)  
  s = validate_series(s)  
  s_transformed = RollingAggregate(agg='quantile',agg_params={"q": [0.25, 0.75]}, window=5).transform(s) 

•  DoubleRollingAggregate 提供了两个窗口之间统计特征的差异特征，如前5分钟和后5分钟，均值的差值等。agg参数和RollingAggregate中一致，新增的参数diff主要衡量差距的函数： 

import pandas as pd  
from adtk.data import validate_series  
from adtk.transformer import DoubleRollingAggregate  
s = pd.read_csv('./data/ec2_cpu_utilization_53ea38.csv', index_col="timestamp", parse_dates=True)  
s = validate_series(s)  
s_transformed = DoubleRollingAggregate(  
    agg="median",  
    window=5,  
    diff="diff").transform(s) 

•  'diff': 后减去前
•  'rel_diff': Relative difference between values of aggregated metric (right minus left divided left). Only applicable if the aggregated metric is scalar.
•  'abs_rel_diff': （后-前）/前， 相对差值
•  'l1': l1正则
•  'l2': l2正则

4.2 季节性拆解

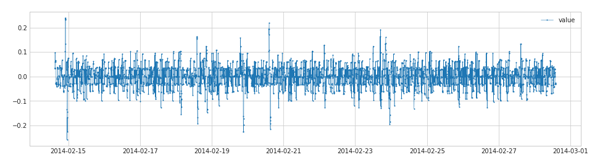
时间序列可拆解成趋势性，季节性和残差部分。atdk中ClassicSeasonalDecomposition提供了这三个部分拆解，并移除趋势和季节性部分，返回残差部分。

•  freq: 设置季节性的周期
•  trend：可以设置是否保留趋势性 

from adtk.transformer import ClassicSeasonalDecomposition  
s = pd.read_csv('./data/nyc_taxi.csv', index_col="timestamp", parse_dates=True)  
s = validate_series(s) 
s_transformed = ClassicSeasonalDecomposition().fit_transform(s) 

 

s_transformed = ClassicSeasonalDecomposition(trend=True).fit_transform(s) 

4.3 降维和重构

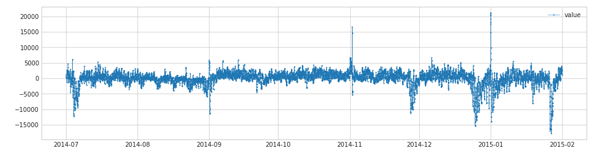
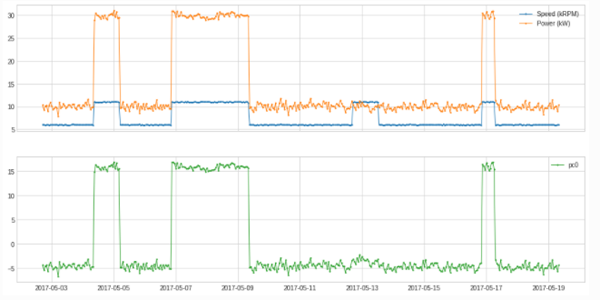
adtk提供的pca对数据进行降维到主成分PcaProjection和重构方法PcaReconstruction。 

df = pd.read_csv('./data/generator.csv', index_col="Time", parse_dates=True)  
df = validate_series(df)  
from adtk.transformer import PcaProjection  
s = PcaProjection(k=1).fit_transform(df)  
plot(pd.concat([df, s], axis=1), ts_linewidth=1, ts_markersize=3, curve_group=[("Speed (kRPM)", "Power (kW)"), "pc0"]); 

 

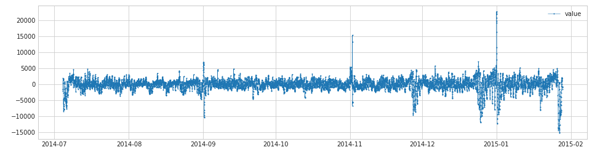
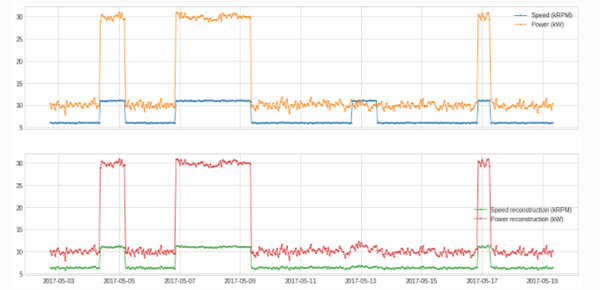
from adtk.transformer import PcaReconstruction  
df_transformed = PcaReconstruction(k=1).fit_transform(df).rename(columns={"Speed (kRPM)": "Speed reconstruction (kRPM)", "Power (kW)": "Power reconstruction (kW)"}) 
plot(pd.concat([df, df_transformed], axis=1), ts_linewidth=1, ts_markersize=3, curve_group=[("Speed (kRPM)", "Power (kW)"), ("Speed reconstruction (kRPM)", "Power reconstruction (kW)")]); 
../_images/notebooks_demo_99_0.png 

5. 异常检测算法（detector）

adtk提供的主要是无监督或者基于规则的时间序列检测算法，可以用于常规的异常检测。

•  检测离群点 离群点是和普通数据差异极大的数据点。adtk主要提供了包括 adtk.detector.ThresholdAD adtk.detector.QuantileAD adtk.detector.InterQuartileRangeAD adtk.detector.GeneralizedESDTestAD的检测算法。
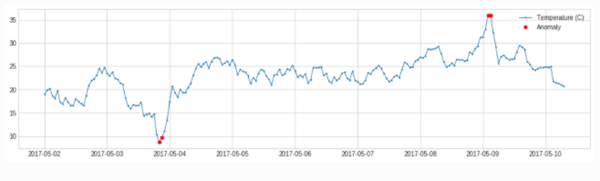
  •  ThresholdAD 

adtk.detector.ThresholdAD(low=None, high=None)  
 参数：  
 low：下限，小于此值，视为异常  
 high：上限，大于此值，视为异常  
 原理：通过认为设定上下限来识别异常  
 总结：固定阈值算法  

from adtk.detector import ThresholdAD  
threshold_ad = ThresholdAD(high=30, low=15)  
anomalies = threshold_ad.detect(s) 

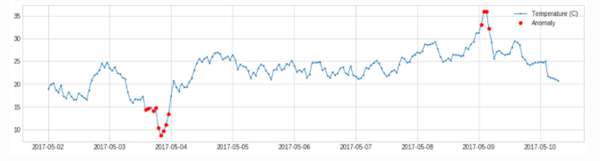
•  QuantileAD 

adtk.detector.QuantileAD(low=None, high=None)  
参数：  
low：分位下限，范围(0,1)，当low=0.25时，表示Q1  
high：分位上限，范围(0,1)，当low=0.25时，表示Q3  
原理：通过历史数据计算出给定low与high对应的分位值Q_low,Q_high，小于Q_low或大于Q_high，视为异常  
总结：分位阈值算法  

from adtk.detector import QuantileAD  
quantile_ad = QuantileAD(high=0.99, low=0.01)  
anomalies = quantile_ad.fit_detect(s) 

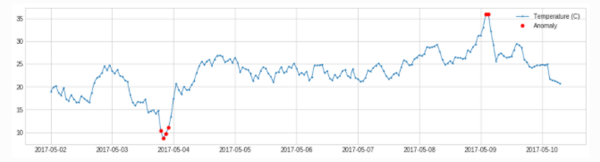
•  InterQuartileRangeAD 

adtk.detector.InterQuartileRangeAD(c=3.0)  
参数：  
c：分位距的系数，用来确定上下限，可为float，也可为(float,float)  
原理： 
当c为float时，通过历史数据计算出 Q3+c*IQR 作为上限值，大于上限值视为异常  
当c=(float1,float2)时，通过历史数据计算出 (Q1-c1*IQR, Q3+c2*IQR) 作为正常范围，不在正常范围视为异常  
总结：箱线图算法  

from adtk.detector import InterQuartileRangeAD  
iqr_ad = InterQuartileRangeAD(c=1.5)  
anomalies = iqr_ad.fit_detect(s) 

•  GeneralizedESDTestAD   

adtk.detector.GeneralizedESDTestAD(alpha=0.05)  
   参数：  
   alpha：显著性水平 (Significance level)，alpha越小，表示识别出的异常约有把握是真异常  
   原理:将样本点的值与样本的均值作差后除以样本标准差，取最大值，通过t分布计算阈值，对比阈值确定异常点  
   计算步骤简述：  
   设置显著水平alpha，通常取0.05  
   指定离群比例h，若h=5%，则表示50各样本中存在离群点数为2  
   计算数据集的均值mu与标准差sigma，将所有样本与均值作差，取绝对值，再除以标准差，找出最大值，得到esd_1  
   在剩下的样本点中，重复步骤3，可以得到h个esd值  
   为每个esd值计算critical value: lambda_i (采用t分布计算)  
   统计每个esd是否大于lambda_i，大于的认为你是异常  

from adtk.detector import GeneralizedESDTestAD  
esd_ad = GeneralizedESDTestAD(alpha=0.3)  
anomalies = esd_ad.fit_detect(s) 

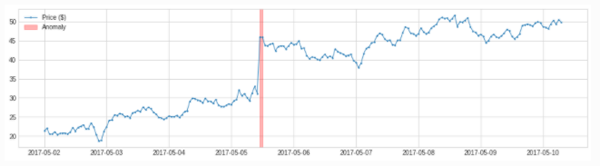
•  突变：Spike and Level Shift 异常的表现形式不是离群点，而是通过和临近点的比较，即突增或者突降。adtk提供adtk.detector.PersistAD 和 adtk.detector.LevelShiftAD检测方法
  
  •  PersistAD   

adtk.detector.PersistAD(window=1, c=3.0, side='both', min_periods=None, agg='median')  
   参数：  
   window：参考窗长度，可为int, str  
   c：分位距倍数，用于确定上下限范围  
   side：检测范围，为'positive'时检测突增，为'negative'时检测突降，为'both'时突增突降都检测  
   min_periods：参考窗中最小个数，小于此个数将会报异常，默认为None，表示每个时间点都得有值  
   agg：参考窗中的统计量计算方式，因为当前值是与参考窗中产生的统计量作比较，所以得将参考窗中的数据计算成统计量，默认'median'，表示去参考窗的中位值  
   原理：  
   用滑动窗口遍历历史数据，将窗口后的一位数据与参考窗中的统计量做差，得到一个新的时间序列s1;  
   计算s1的(Q1-c*IQR, Q3+c*IQR) 作为正常范围； 
   若当前值与它参考窗中的统计量之差，不在2中的正常范围内，视为异常。  
   调参：  
   window：越大，模型越不敏感，不容易被突刺干扰  
   c：越大，对于波动大的数据，正常范围放大较大，对于波动较小的数据，正常范围放大较小  
   min_periods：对缺失值的容忍程度，越大，越不允许有太多的缺失值  
   agg：统计量的聚合方式，跟统计量的特性有关，如 'median'不容易受极端值影响  
   总结：先计算一条新的时间序列，再用箱线图作异常检测  

from adtk.detector import PersistAD  
persist_ad = PersistAD(c=3.0, side='positive')  
anomalies = persist_ad.fit_detect(s) 

•  LevelShiftAD 

adtk.detector.LevelShiftAD(window, c=6.0, side='both', min_periods=None)  
 参数：  
 window：支持(10,5)，表示使用两个相邻的滑动窗，左侧的窗中的中位值表示参考值，右侧窗中的中位值表示当前值  
 c：越大，对于波动大的数据，正常范围放大较大，对于波动较小的数据，正常范围放大较小，默认6.0  
 side：检测范围，为'positive'时检测突增，为'negative'时检测突降，为'both'时突增突降都检测  
 min_periods：参考窗中最小个数，小于此个数将会报异常，默认为None，表示每个时间点都得有值  
 原理： 
 该模型用于检测突变情况，相比于PersistAD，其抗抖动能力较强，不容易出现误报  

from adtk.detector import LevelShiftAD  
level_shift_ad = LevelShiftAD(c=6.0, side='both', window=5)  
anomalies = level_shift_ad.fit_detect(s) 

•  季节性
  
  •  adtk.detector.SeasonalAD 

adtk.detector.SeasonalAD(freq=None, side='both', c=3.0, trend=False)  
SeasonalAD主要是根据ClassicSeasonalDecomposition来处理，判断。  
参数：  
freq：季节性周期  
c：越大，对于波动大的数据，正常范围放大较大，对于波动较小的数据，正常范围放大较小，默认6.0  
side：检测范围，为'positive'时检测突增，为'negative'时检测突降，为'both'时突增突降都检测  
trend： 是否考虑趋势      

from adtk.detector import SeasonalAD  
      seasonal_ad = SeasonalAD(c=3.0, side="both")  
      anomalies = seasonal_ad.fit_detect(s)  
      plot(s, anomaly=anomalies, ts_markersize=1, anomaly_color='red', anomaly_tag="marker", anomaly_markersize=2); 

•  pipe 组合算法   

from adtk.pipe import Pipeline  
   steps = [  
       ("deseasonal", ClassicSeasonalDecomposition()),  
       ("quantile_ad", QuantileAD(high=0.995, low=0.005))  
   ] 
   pipeline = Pipeline(steps)  
   anomalies = pipeline.fit_detect(s)  
   plot(s, anomaly=anomalies, ts_markersize=1, anomaly_markersize=2, anomaly_tag="marker", anomaly_color='red'); 

6. 总结

本文介绍了时间序列异常检测的无监督算法工具包ADTK。ADTK提供了简单的异常检测算法和时间序列特征加工函数，希望对你有帮助。总结如下：

•  adtk要求输入数据为datetimeIndex，validate_series来验证数据有效性，使得时间有序
•  adtk单窗口和double窗口滑动，加工统计特征
•  adtk分解时间序列的季节部分，获得时间序列的残差部分，可根据这个判断异常点
•  adtk支持离群点、突变和季节性异常检测。通过fit_detect 获取异常点序列，也可以通过Pipeline联通多部异常检测算法