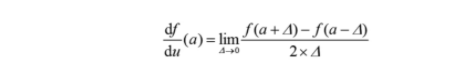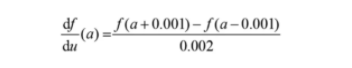让我们从一道选择题开始今天的话题。
什么是神经网络?
请选择以下描述正确的一项或多项。
A.神经网络是一种数学函数,它接收输入并产生输出。
B.神经网络是一种计算图,多维数组流经其中。
C.神经网络由层组成,每层都具有「神经元」。
D.神经网络是一种通用函数逼近器。
你的答案是________。
公布答案了哈,正确答案是……ABCD。
是不是有点懵?对于神经网络,难道就没有唯一、统一的描述吗?
塞思·韦德曼(Seth Weidman)是前Facebook数据科学家。他曾受邀走访世界各地,为来自不同行业的人们讲授数据科学和机器学习。
前Facebook数据科学家塞思·韦德曼 图源:sethweidman.com
在其著作《Python深度学习入门:从零构建CNN和RNN》中,韦德曼写道:
对于讲解神经网络,我发现最具挑战性的就是为「什么是神经网络」传达正确的思维模型。这主要是因为,了解神经网络需要的不是一个而是多个思维模型,每一个都说明了神经网络工作方式的不同方面(而且每个方面都必不可少)。
诚然,神经网络与深度学习是一个立体的领域,仅从数学层面或代码层面学习,难免以偏概全,无法融会贯通。正因为如此,韦德曼提出了一种全新的学习方法:同时从数学、示意图、Python代码三个维度立体地理解每一个概念,从而领略深度学习领域的全貌。
想象你要构建自己的深度学习大厦。你或许钟情于算法,又或许习惯于视觉型学习,但唯有进行「升维思考」,你才能建造出多面玲珑的建筑。
韦德曼提出以如下步骤学习导数、嵌套函数、链式法则等概念。这些基本概念就如同一块块砖,有了它们,你终将建造出属于自己的深度学习大厦。
- 以一个或多个方程式展示数学原理。
- 给出示意图,类似于在参加编码面试时画在白板上的图。
- 给出对应的Python代码。
让我们一起看看用这种学习方法如何理解导数的概念。
导数是深度学习的一个非常重要的概念。总体来说,函数在某一点上的导数,可以简单地看作函数输出相对于该点输入的「变化率」。
维度1:数学
首先在数学维度上定义导数。可以使用一个数来描述极限,即当改变某个特定的输入值 时,函数 的输出有多大变化:
通过为Δ设置非常小的值(例如0.001),可以在数值上近似此极限。因此,如果Δ=0.001,就可以将导数计算为:
虽然近似准确,但这只是完整导数思维模型的一部分。下面来从示意图的维度认识导数。
维度2:示意图
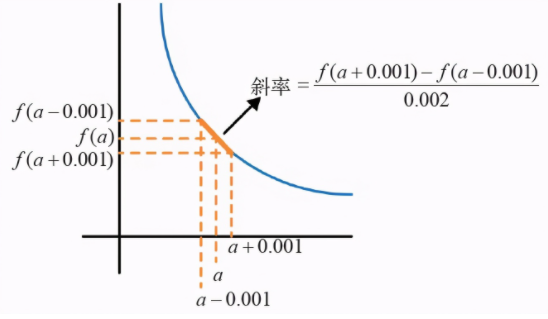
为函数曲线画出一条切线,则函数f 在点a 处的导数就是该线在点a 处的斜率。可以通过两种方式来计算这条线的斜率。第一种方式是使用微积分来实际计算极限,第二种方式是在a−0.001处和a+0.001处取连线f 的斜率,如下图所示。
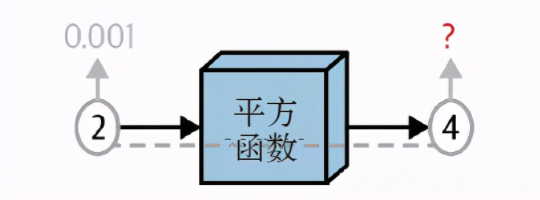
另一种可视化方式是将函数想象成小型工厂,并想象其输入通过一根线连接到输出。求解导数相当于回答这样一个问题:如果将函数的输入a拉高一点,那么根据工厂的内部运作机制,输出量将以这个小数值的多少倍进行变化呢?
对理解深度学习而言,第二种表示形式比第一种更为重要。
维度3:Python代码
可以通过编码来求解前面看到的导数的近似值:
当我们说P 是E(随机选的字母)的函数时,其实是指存在某个函数f,使得f (E ) =P。或者说,有一个函数f,它接收对象E 并产生对象P。也可以说,P 是函数f 应用于E 时产生的任意函数值:
可以将其编码为下面这种形式。