预测间隔为回归问题的预测提供了不确定性度量。
例如,95%的预测间隔表示100次中的95次,真实值将落在该范围的下限值和上限值之间。这不同于可能表示不确定性区间中心的简单点预测。没有用于计算深度学习神经网络关于回归预测建模问题的预测间隔的标准技术。但是,可以使用一组模型来估计快速且肮脏的预测间隔,这些模型又提供了点预测的分布,可以从中计算间隔。
在本教程中,您将发现如何计算深度学习神经网络的预测间隔。完成本教程后,您将知道:
- 预测间隔为回归预测建模问题提供了不确定性度量。
- 如何在标准回归问题上开发和评估简单的多层感知器神经网络。
- 如何使用神经网络模型集成来计算和报告预测间隔。
教程概述
本教程分为三个部分:他们是:
- 预测间隔
- 回归神经网络
- 神经网络预测间隔
预测间隔
通常,用于回归问题的预测模型(即预测数值)进行点预测。这意味着他们可以预测单个值,但不能提供任何有关该预测的不确定性的指示。根据定义,预测是估计值或近似值,并且包含一些不确定性。不确定性来自模型本身的误差和输入数据中的噪声。该模型是输入变量和输出变量之间关系的近似值。预测间隔是对预测不确定性的量化。它为结果变量的估计提供了概率上限和下限。
预测间隔是在预测数量的回归模型中进行预测或预测时最常使用的时间间隔。预测间隔围绕模型所做的预测,并希望覆盖真实结果的范围。有关一般的预测间隔的更多信息,请参见教程:
《机器学习的预测间隔》:
https://machinelearningmastery.com/prediction-intervals-for-machine-learning/
既然我们熟悉了预测间隔,那么我们可以考虑如何计算神经网络的间隔。首先定义一个回归问题和一个神经网络模型来解决这个问题。
回归神经网络
在本节中,我们将定义回归预测建模问题和神经网络模型来解决该问题。首先,让我们介绍一个标准回归数据集。我们将使用住房数据集。住房数据集是一个标准的机器学习数据集,包括506行数据,其中包含13个数字输入变量和一个数字目标变量。
使用具有三个重复的重复分层10倍交叉验证的测试工具,一个朴素的模型可以实现约6.6的平均绝对误差(MAE)。在大约1.9的相同测试工具上,性能最高的模型可以实现MAE。这为该数据集提供了预期性能的界限。该数据集包括根据美国波士顿市房屋郊区的详细信息来预测房价。
房屋数据集(housing.csv):
https://raw.githubusercontent.com/jbrownlee/Datasets/master/housing.csv
房屋描述(房屋名称):
https://raw.githubusercontent.com/jbrownlee/Datasets/master/housing.names
无需下载数据集;作为我们工作示例的一部分,我们将自动下载它。
下面的示例将数据集下载并加载为Pandas DataFrame,并概述了数据集的形状和数据的前五行。
# load and summarize the housing dataset
from pandas import read_csv
from matplotlib import pyplot
# load dataset
url = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/housing.csv'
dataframe = read_csv(url, header=None)
# summarize shape
print(dataframe.shape)
# summarize first few lines
print(dataframe.head())
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
运行示例将确认506行数据和13个输入变量以及一个数字目标变量(总共14个)。我们还可以看到所有输入变量都是数字。
(506, 14)
0 1 2 3 4 5 ... 8 9 10 11 12 13
0 0.00632 18.0 2.31 0 0.538 6.575 ... 1 296.0 15.3 396.90 4.98 24.0
1 0.02731 0.0 7.07 0 0.469 6.421 ... 2 242.0 17.8 396.90 9.14 21.6
2 0.02729 0.0 7.07 0 0.469 7.185 ... 2 242.0 17.8 392.83 4.03 34.7
3 0.03237 0.0 2.18 0 0.458 6.998 ... 3 222.0 18.7 394.63 2.94 33.4
4 0.06905 0.0 2.18 0 0.458 7.147 ... 3 222.0 18.7 396.90 5.33 36.2
[5 rows x 14 columns]
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
接下来,我们可以准备用于建模的数据集。首先,可以将数据集拆分为输入和输出列,然后可以将行拆分为训练和测试数据集。在这种情况下,我们将使用约67%的行来训练模型,而其余33%的行用于估计模型的性能。
# split into input and output values
X, y = values[:,:-1], values[:,-1]
# split into train and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.67)
- 1.
- 2.
- 3.
- 4.
您可以在本教程中了解有关训练测试拆分的更多信息:训练测试拆分以评估机器学习算法然后,我们将所有输入列(变量)缩放到0-1范围,称为数据归一化,这在使用神经网络模型时是一个好习惯。
# scale input data
scaler = MinMaxScaler()
scaler.fit(X_train)
X_train = scaler.transform(X_train)
X_test = scaler.transform(X_test)
- 1.
- 2.
- 3.
- 4.
- 5.
您可以在本教程中了解有关使用MinMaxScaler标准化输入数据的更多信息:《如何在Python中使用StandardScaler和MinMaxScaler转换 》:
https://machinelearningmastery.com/standardscaler-and-minmaxscaler-transforms-in-python/
下面列出了准备用于建模的数据的完整示例。
# load and prepare the dataset for modeling
from pandas import read_csv
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import MinMaxScaler
# load dataset
url = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/housing.csv'
dataframe = read_csv(url, header=None)
values = dataframe.values
# split into input and output values
X, y = values[:,:-1], values[:,-1]
# split into train and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.67)
# scale input data
scaler = MinMaxScaler()
scaler.fit(X_train)
X_train = scaler.transform(X_train)
X_test = scaler.transform(X_test)
# summarize
print(X_train.shape, X_test.shape, y_train.shape, y_test.shape)
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
运行示例像以前一样加载数据集,然后将列拆分为输入和输出元素,将行拆分为训练集和测试集,最后将所有输入变量缩放到[0,1]范围。列印了训练图和测试集的形状,显示我们有339行用于训练模型,有167行用于评估模型。
(339, 13) (167, 13) (339,) (167,)
- 1.
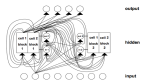
接下来,我们可以在数据集中定义,训练和评估多层感知器(MLP)模型。我们将定义一个简单的模型,该模型具有两个隐藏层和一个预测数值的输出层。我们将使用ReLU激活功能和“ he”权重初始化,这是一个好习惯。经过一些反复试验后,选择了每个隐藏层中的节点数。
# define neural network model
features = X_train.shape[1]
model = Sequential()
model.add(Dense(20, kernel_initializer='he_normal', activation='relu', input_dim=features))
model.add(Dense(5, kernel_initializer='he_normal', activation='relu'))
model.add(Dense(1))
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
我们将使用具有接近默认学习速率和动量值的高效亚当版随机梯度下降法,并使用均方误差(MSE)损失函数(回归预测建模问题的标准)拟合模型。
# compile the model and specify loss and optimizer
opt = Adam(learning_rate=0.01, beta_1=0.85, beta_2=0.999)
model.compile(optimizer=opt, loss='mse')
- 1.
- 2.
- 3.
您可以在本教程中了解有关Adam优化算法的更多信息:
《从头开始编写代码Adam梯度下降优化》
https://machinelearningmastery.com/adam-optimization-from-scratch/
然后,该模型将适合300个纪元,批处理大小为16个样本。经过一番尝试和错误后,才选择此配置。
# fit the model on the training dataset
model.fit(X_train, y_train, verbose=2, epochs=300, batch_size=16)
- 1.
- 2.
您可以在本教程中了解有关批次和纪元的更多信息:
《神经网络中批次与时期之间的差异》
https://machinelearningmastery.com/difference-between-a-batch-and-an-epoch/
最后,该模型可用于在测试数据集上进行预测,我们可以通过将预测值与测试集中的预期值进行比较来评估预测,并计算平均绝对误差(MAE),这是模型性能的一种有用度量。
# make predictions on the test set
yhat = model.predict(X_test, verbose=0)
# calculate the average error in the predictions
mae = mean_absolute_error(y_test, yhat)
print('MAE: %.3f' % mae)
- 1.
- 2.
- 3.
- 4.
- 5.
完整实例如下:
# train and evaluate a multilayer perceptron neural network on the housing regression dataset
from pandas import read_csv
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_absolute_error
from sklearn.preprocessing import MinMaxScaler
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
from tensorflow.keras.optimizers import Adam
# load dataset
url = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/housing.csv'
dataframe = read_csv(url, header=None)
values = dataframe.values
# split into input and output values
X, y = values[:, :-1], values[:,-1]
# split into train and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.67, random_state=1)
# scale input data
scaler = MinMaxScaler()
scaler.fit(X_train)
X_train = scaler.transform(X_train)
X_test = scaler.transform(X_test)
# define neural network model
features = X_train.shape[1]
model = Sequential()
model.add(Dense(20, kernel_initializer='he_normal', activation='relu', input_dim=features))
model.add(Dense(5, kernel_initializer='he_normal', activation='relu'))
model.add(Dense(1))
# compile the model and specify loss and optimizer
opt = Adam(learning_rate=0.01, beta_1=0.85, beta_2=0.999)
model.compile(optimizer=opt, loss='mse')
# fit the model on the training dataset
model.fit(X_train, y_train, verbose=2, epochs=300, batch_size=16)
# make predictions on the test set
yhat = model.predict(X_test, verbose=0)
# calculate the average error in the predictions
mae = mean_absolute_error(y_test, yhat)
print('MAE: %.3f' % mae)
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
- 25.
- 26.
- 27.
- 28.
- 29.
- 30.
- 31.
- 32.
- 33.
- 34.
- 35.
- 36.
- 37.
运行示例将加载并准备数据集,在训练数据集上定义MLP模型并将其拟合,并在测试集上评估其性能。
注意:由于算法或评估程序的随机性,或者数值精度的差异,您的结果可能会有所不同。考虑运行该示例几次并比较平均结果。
在这种情况下,我们可以看到该模型实现的平均绝对误差约为2.3,这比朴素的模型要好,并且接近于最佳模型。
毫无疑问,通过进一步调整模型,我们可以达到接近最佳的性能,但这对于我们研究预测间隔已经足够了。
Epoch 296/300
22/22 - 0s - loss: 7.1741
Epoch 297/300
22/22 - 0s - loss: 6.8044
Epoch 298/300
22/22 - 0s - loss: 6.8623
Epoch 299/300
22/22 - 0s - loss: 7.7010
Epoch 300/300
22/22 - 0s - loss: 6.5374
MAE: 2.300
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
接下来,让我们看看如何使用住房数据集上的MLP模型计算预测间隔。
神经网络预测间隔
在本节中,我们将使用上一节中开发的回归问题和模型来开发预测间隔。
与像线性回归这样的线性方法(预测间隔计算很简单)相比,像神经网络这样的非线性回归算法的预测间隔计算具有挑战性。没有标准技术。有许多方法可以为神经网络模型计算有效的预测间隔。我建议“更多阅读”部分列出的一些论文以了解更多信息。
在本教程中,我们将使用一种非常简单的方法,该方法具有很大的扩展空间。我将其称为“快速且肮脏的”,因为它快速且易于计算,但有一定的局限性。它涉及拟合多个最终模型(例如10到30)。来自集合成员的点预测的分布然后用于计算点预测和预测间隔。
例如,可以将点预测作为来自集合成员的点预测的平均值,并且可以将95%的预测间隔作为与该平均值的1.96标准偏差。这是一个简单的高斯预测间隔,尽管可以使用替代方法,例如点预测的最小值和最大值。或者,可以使用自举方法在不同的自举样本上训练每个合奏成员,并且可以将点预测的第2.5个百分点和第97.5个百分点用作预测间隔。
有关bootstrap方法的更多信息,请参见教程:
《Bootstrap方法的简要介绍》
https://machinelearningmastery.com/a-gentle-introduction-to-the-bootstrap-method/
这些扩展保留为练习;我们将坚持简单的高斯预测区间。
假设在上一部分中定义的训练数据集是整个数据集,并且我们正在对该整个数据集训练一个或多个最终模型。然后,我们可以在测试集上使用预测间隔进行预测,并评估该间隔在将来的有效性。
我们可以通过将上一节中开发的元素划分为功能来简化代码。首先,让我们定义一个函数,以加载和准备由URL定义的回归数据集。
# load and prepare the dataset
def load_dataset(url):
dataframe = read_csv(url, header=None)
values = dataframe.values
# split into input and output values
X, y = values[:, :-1], values[:,-1]
# split into train and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.67, random_state=1)
# scale input data
scaler = MinMaxScaler()
scaler.fit(X_train)
X_train = scaler.transform(X_train)
X_test = scaler.transform(X_test)
return X_train, X_test, y_train, y_test
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
接下来,我们可以定义一个函数,该函数将在给定训练数据集的情况下定义和训练MLP模型,然后返回适合进行预测的拟合模型。
# define and fit the model
def fit_model(X_train, y_train):
# define neural network model
features = X_train.shape[1]
model = Sequential()
model.add(Dense(20, kernel_initializer='he_normal', activation='relu', input_dim=features))
model.add(Dense(5, kernel_initializer='he_normal', activation='relu'))
model.add(Dense(1))
# compile the model and specify loss and optimizer
opt = Adam(learning_rate=0.01, beta_1=0.85, beta_2=0.999)
model.compile(optimizer=opt, loss='mse')
# fit the model on the training dataset
model.fit(X_train, y_train, verbose=0, epochs=300, batch_size=16)
return model
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
我们需要多个模型来进行点预测,这些模型将定义点预测的分布,从中可以估计间隔。
因此,我们需要在训练数据集上拟合多个模型。每个模型必须不同,以便做出不同的预测。在训练MLP模型具有随机性,随机初始权重以及使用随机梯度下降优化算法的情况下,可以实现这一点。模型越多,点预测将更好地估计模型的功能。我建议至少使用10种型号,而超过30种型号可能不会带来太多好处。下面的函数适合模型的整体,并将其存储在返回的列表中。出于兴趣,还对测试集评估了每个拟合模型,并在拟合每个模型后报告了该测试集。我们希望每个模型在保持测试集上的估计性能会略有不同,并且报告的分数将有助于我们确认这一期望。
# fit an ensemble of models
def fit_ensemble(n_members, X_train, X_test, y_train, y_test):
ensemble = list()
for i in range(n_members):
# define and fit the model on the training set
model = fit_model(X_train, y_train)
# evaluate model on the test set
yhat = model.predict(X_test, verbose=0)
mae = mean_absolute_error(y_test, yhat)
print('>%d, MAE: %.3f' % (i+1, mae))
# store the model
ensemble.append(model)
return ensemble
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
最后,我们可以使用训练有素的模型集合进行点预测,可以将其总结为一个预测区间。
下面的功能实现了这一点。首先,每个模型对输入数据进行点预测,然后计算95%的预测间隔,并返回该间隔的下限值,平均值和上限值。
该函数被设计为将单行作为输入,但是可以很容易地适应于多行。
# make predictions with the ensemble and calculate a prediction interval
def predict_with_pi(ensemble, X):
# make predictions
yhat = [model.predict(X, verbose=0) for model in ensemble]
yhat = asarray(yhat)
# calculate 95% gaussian prediction interval
interval = 1.96 * yhat.std()
lower, upper = yhat.mean() - interval, yhat.mean() + interval
return lower, yhat.mean(), upper
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
最后,我们可以调用这些函数。首先,加载并准备数据集,然后定义并拟合集合。
# load dataset
url = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/housing.csv'
X_train, X_test, y_train, y_test = load_dataset(url)
# fit ensemble
n_members = 30
ensemble = fit_ensemble(n_members, X_train, X_test, y_train, y_test)
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
然后,我们可以使用测试集中的一行数据,并以预测间隔进行预测,然后报告结果。
我们还报告了预期的期望值,该期望值将在预测间隔内涵盖(可能接近95%的时间;这并不完全准确,而是粗略的近似值)。
# make predictions with prediction interval
newX = asarray([X_test[0, :]])
lower, mean, upper = predict_with_pi(ensemble, newX)
print('Point prediction: %.3f' % mean)
print('95%% prediction interval: [%.3f, %.3f]' % (lower, upper))
print('True value: %.3f' % y_test[0])
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
综上所述,下面列出了使用多层感知器神经网络以预测间隔进行预测的完整示例。
# prediction interval for mlps on the housing regression dataset
from numpy import asarray
from pandas import read_csv
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_absolute_error
from sklearn.preprocessing import MinMaxScaler
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
from tensorflow.keras.optimizers import Adam
# load and prepare the dataset
def load_dataset(url):
dataframe = read_csv(url, header=None)
values = dataframe.values
# split into input and output values
X, y = values[:, :-1], values[:,-1]
# split into train and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.67, random_state=1)
# scale input data
scaler = MinMaxScaler()
scaler.fit(X_train)
X_train = scaler.transform(X_train)
X_test = scaler.transform(X_test)
return X_train, X_test, y_train, y_test
# define and fit the model
def fit_model(X_train, y_train):
# define neural network model
features = X_train.shape[1]
model = Sequential()
model.add(Dense(20, kernel_initializer='he_normal', activation='relu', input_dim=features))
model.add(Dense(5, kernel_initializer='he_normal', activation='relu'))
model.add(Dense(1))
# compile the model and specify loss and optimizer
opt = Adam(learning_rate=0.01, beta_1=0.85, beta_2=0.999)
model.compile(optimizer=opt, loss='mse')
# fit the model on the training dataset
model.fit(X_train, y_train, verbose=0, epochs=300, batch_size=16)
return model
# fit an ensemble of models
def fit_ensemble(n_members, X_train, X_test, y_train, y_test):
ensemble = list()
for i in range(n_members):
# define and fit the model on the training set
model = fit_model(X_train, y_train)
# evaluate model on the test set
yhat = model.predict(X_test, verbose=0)
mae = mean_absolute_error(y_test, yhat)
print('>%d, MAE: %.3f' % (i+1, mae))
# store the model
ensemble.append(model)
return ensemble
# make predictions with the ensemble and calculate a prediction interval
def predict_with_pi(ensemble, X):
# make predictions
yhat = [model.predict(X, verbose=0) for model in ensemble]
yhat = asarray(yhat)
# calculate 95% gaussian prediction interval
interval = 1.96 * yhat.std()
lower, upper = yhat.mean() - interval, yhat.mean() + interval
return lower, yhat.mean(), upper
# load dataset
url = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/housing.csv'
X_train, X_test, y_train, y_test = load_dataset(url)
# fit ensemble
n_members = 30
ensemble = fit_ensemble(n_members, X_train, X_test, y_train, y_test)
# make predictions with prediction interval
newX = asarray([X_test[0, :]])
lower, mean, upper = predict_with_pi(ensemble, newX)
print('Point prediction: %.3f' % mean)
print('95%% prediction interval: [%.3f, %.3f]' % (lower, upper))
print('True value: %.3f' % y_test[0])
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
- 25.
- 26.
- 27.
- 28.
- 29.
- 30.
- 31.
- 32.
- 33.
- 34.
- 35.
- 36.
- 37.
- 38.
- 39.
- 40.
- 41.
- 42.
- 43.
- 44.
- 45.
- 46.
- 47.
- 48.
- 49.
- 50.
- 51.
- 52.
- 53.
- 54.
- 55.
- 56.
- 57.
- 58.
- 59.
- 60.
- 61.
- 62.
- 63.
- 64.
- 65.
- 66.
- 67.
- 68.
- 69.
- 70.
- 71.
- 72.
- 73.
- 74.
- 75.
- 76.
运行示例依次适合每个集合成员,并在保留测试集上报告其估计性能;最后,做出并预测一个具有预测间隔的预测。
注意:由于算法或评估程序的随机性,或者数值精度的差异,您的结果可能会有所不同。考虑运行该示例几次并比较平均结果。
在这种情况下,我们可以看到每个模型的性能略有不同,这证实了我们对模型确实有所不同的期望。
最后,我们可以看到该合奏以95%的预测间隔[26.287,34.822]进行了约30.5的点预测。我们还可以看到,真实值为28.2,并且间隔确实捕获了该值,这非常好。
>1, MAE: 2.259
>2, MAE: 2.144
>3, MAE: 2.732
>4, MAE: 2.628
>5, MAE: 2.483
>6, MAE: 2.551
>7, MAE: 2.505
>8, MAE: 2.299
>9, MAE: 2.706
>10, MAE: 2.145
>11, MAE: 2.765
>12, MAE: 3.244
>13, MAE: 2.385
>14, MAE: 2.592
>15, MAE: 2.418
>16, MAE: 2.493
>17, MAE: 2.367
>18, MAE: 2.569
>19, MAE: 2.664
>20, MAE: 2.233
>21, MAE: 2.228
>22, MAE: 2.646
>23, MAE: 2.641
>24, MAE: 2.492
>25, MAE: 2.558
>26, MAE: 2.416
>27, MAE: 2.328
>28, MAE: 2.383
>29, MAE: 2.215
>30, MAE: 2.408
Point prediction: 30.555
95% prediction interval: [26.287, 34.822]
True value: 28.200
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
- 25.
- 26.
- 27.
- 28.
- 29.
- 30.
- 31.
- 32.
- 33.
True value: 28.200