如我们所知,JavaScript是当今流行语言中对函数式编程支持最好的编程语言。而函数式编程"从一到无穷”的起点是 reduce,本文我们将尝试从 reduce 起步构建所有的其他函数。
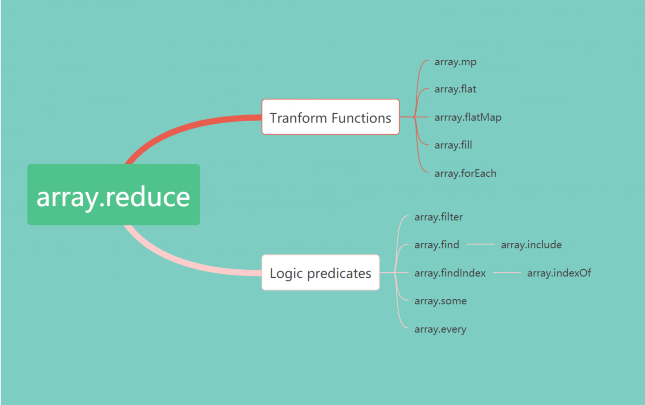
一、万物之始 array.reduce 的应用
Reduce的核心在于降维,将数组reduce为一个值,比如求和:
- const arr = [52, 71, 27, 38];
- const sum = (x, y) => x + y;
- const cusSum = arr.reduce(sum, 0);
将reduce作为思考工具,脑子中要始终留有 initial-value 初始值。
二、构建 array.map 从数学到编程
map是数学思维而直接入编程,从reduce中模拟构建为:
- const cusMap = (arr, fn)
- => arr.reduce((x, y)
- => x.concat(fn(y)), []);
三、构建 array.flat array.flatMap 拍平数组
从array.flat我们窥探到 declaratively 编程的优势,只须将精力专注到要完成的任务上,而不必理会实现细节。用 reduce 实现为:
当只 flat 到一层深度时候:
- # flat only to one level
- const flat1 = arr => [].concat(...arr);
- const flat2 = arr = arr.reduce(acc, v => acc.concat(v), [])
当需要 flat 到任意深度时, 用 reduce 完全重构 flat:
- if (!Array.prototype.flat) {
- Array.prototype.flat = function(n = 1) {
- this.flatAllX = () =>
- this.reduce(
- (f, v) => f.concat(Array.isArray(v) ? v.flat(Infinity) : v),
- []
- );
- this.flatOneX = () => this.reduce((f, v) => f.concat(v), []);
- return n === Infinity
- ? this.flatAllX()
- : n === 1
- ? this.flatOneX()
- : this.flatOneX().flat(n - 1);
- };
- }
四、array.filter 迈向高阶的逻辑判断 logic predicate
为什么要用 reduce 重新构建,因为能够帮助在头脑中始终擦亮 function 与 最终输出 acculator 的概念。
- const cusFilter = (arr, fn)
- => arr.reduce((acc, val)
- => (fn(val) ? acc.concat(y)
- : acc), []);
五、array.find 与 array.findIndex 只找出首个元素
array.filter将会筛选出来全部的符合要求的元素,当我们只要单个元素的时候则应用 array.find.
- const cusFind = arr.reduce((acc, val)
- => (acc === undefined && fn(val) ? val
- : acc), undefined);
重新构建 array.findIndex:
- const cusFindIndex = arr.reduce((x, y, i)
- => (x == -1 && fn(y) ? i
- : x), -1);
进而,我们用 find 与 findIndex 简单的构建 includes 与 indexOf。
- arr.includes(value); // arr.find(v => v === value)
- arr.indexOf(value); // arr.findIndex(v => v === value)
六、快捷的 array.some 与 array.every
array 与 some 两函数虽然简单,思考和使用的时候尤其顺手。
- // arr.every(fn);
- arr.reduce((a, v) => a && fn(v), true); // a for accumulator,
- // arr.some(fn);
- arr.reduce((a, v) => a|| fn(v), false); // v for value
至此,我们从reduce出发,将其他几个高阶函数全部模拟出来,reduce模拟帮助我们强化对每个函数中输入的arguments与输出的 result 的辨识。