在Python中使用逆变换方法生成随机变量-python生成随机整数

目标

在仿真理论中，生成随机变量是最重要的“构建块”之一，而这些随机变量大多是由均匀分布的随机变量生成的。其中一种可以用来产生随机变量的方法是逆变换法。在本文中，我将向您展示如何使用Python中的逆变换方法生成随机变量(包括离散和连续的情况)。

[[388329]]

概念

给定随机变量U，其中U在(0,1)中均匀分布。假设我们要生成随机变量X，其中累积分布函数(CDF)为：

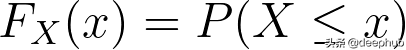
逆变换方法的思想是通过如下使用其逆CDF从任何概率分布中生成一个随机数。

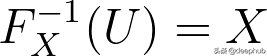
对于离散随机变量，步骤略有不同。假设我们想生成一个离散随机变量X的值，它具有一个概率质量函数(PMF)

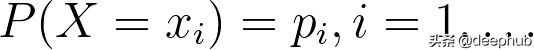
为了生成X的值，需要生成一个随机变量U，U在(0,1)中均匀分布，并且定义

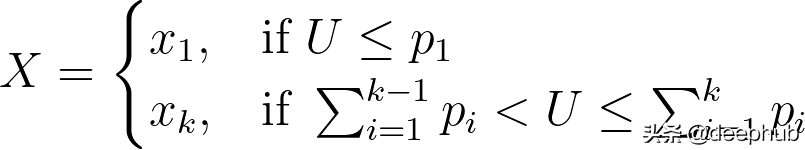
通过以上步骤，我们可以按如下方法创建逆变换方法的算法。

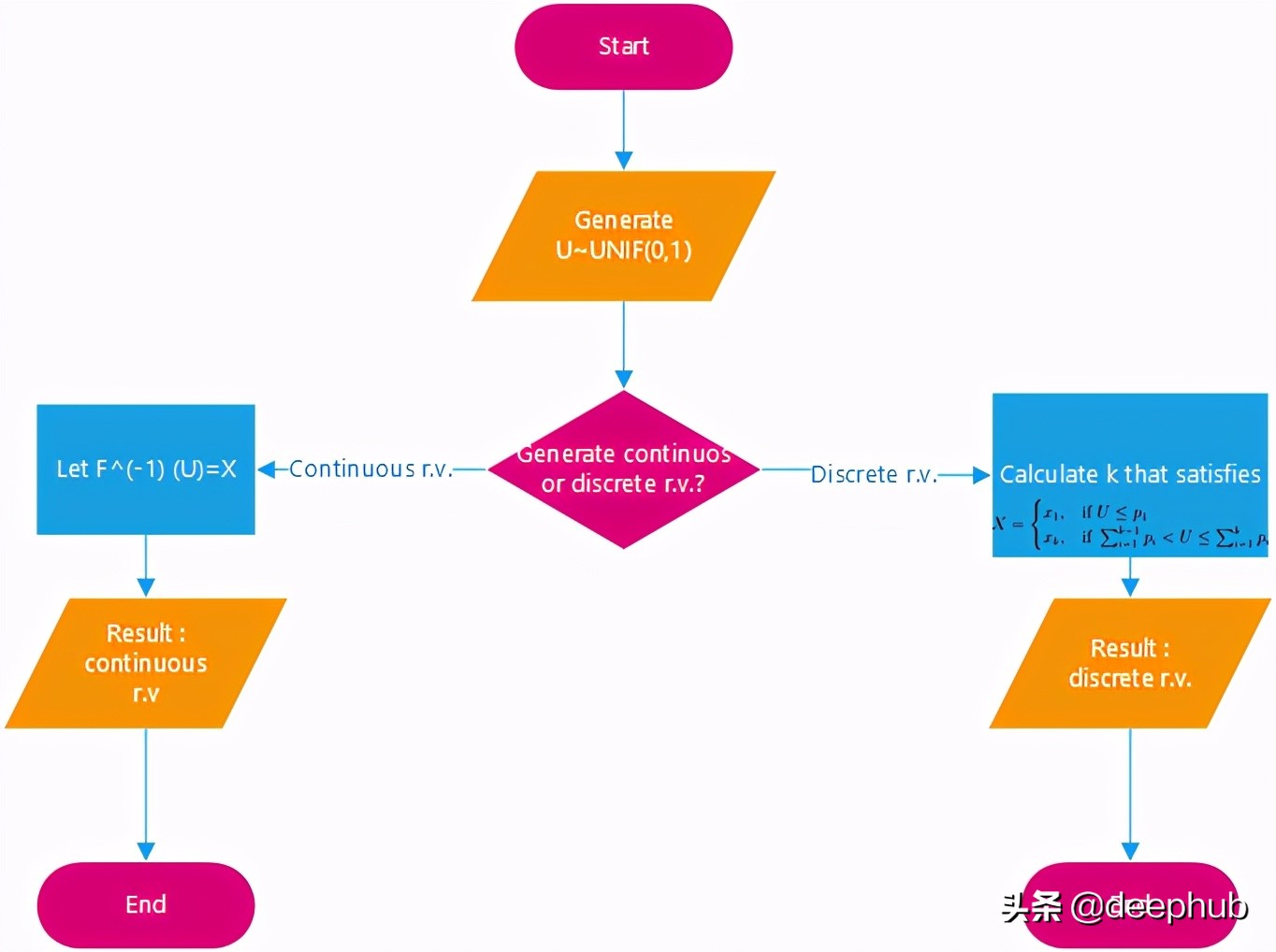
连续随机数代码实现

首先，我们实现此方法以生成连续随机变量。假设我们要模拟一个随机变量X，该变量遵循均值λ(即X〜EXP(λ))的指数分布。我们知道指数分布的概率分布函数(PDF)是

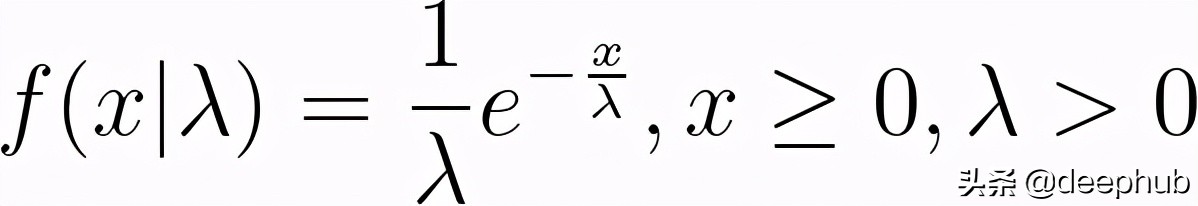
CDF如下

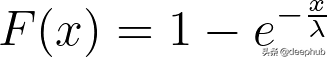
然后，我们可以使用以下的方法写出逆CDF

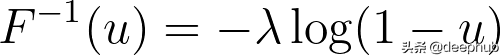
在Python中，我们可以通过如下编写这些代码行来简单地实现它。

### Generate exponential distributed random variables given the mean  
### and number of random variables  
def exponential_inverse_trans(n=1,mean=1):  
U=uniform.rvs(size=n)  
X=-mean*np.log(1-U)  
actual=expon.rvs(size=n,scale=mean)  
 
plt.figure(figsize=(12,9))  
plt.hist(X, bins=50, alpha=0.5, label="Generated r.v.")  
plt.hist(actual, bins=50, alpha=0.5, label="Actual r.v.")  
plt.title("Generated vs Actual %i Exponential Random Variables" %n)  
plt.legend()  
plt.show()  
return X

我们可以通过运行以下示例来尝试上面的代码。请注意，由于我们要生成随机变量，因此结果可能会有所不同。

cont_example1=exponential_inverse_trans(n=100,mean=4)  
cont_example2=exponential_inverse_trans(n=500,mean=4)  
cont_example3=exponential_inverse_trans(n=1000,mean=4)

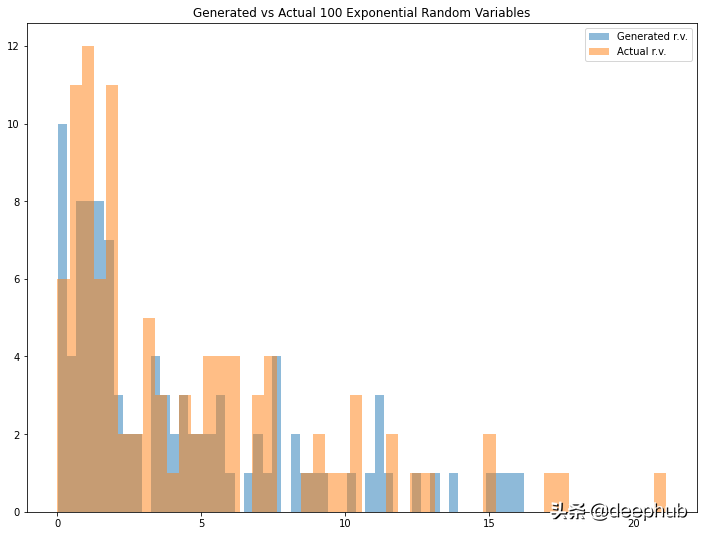
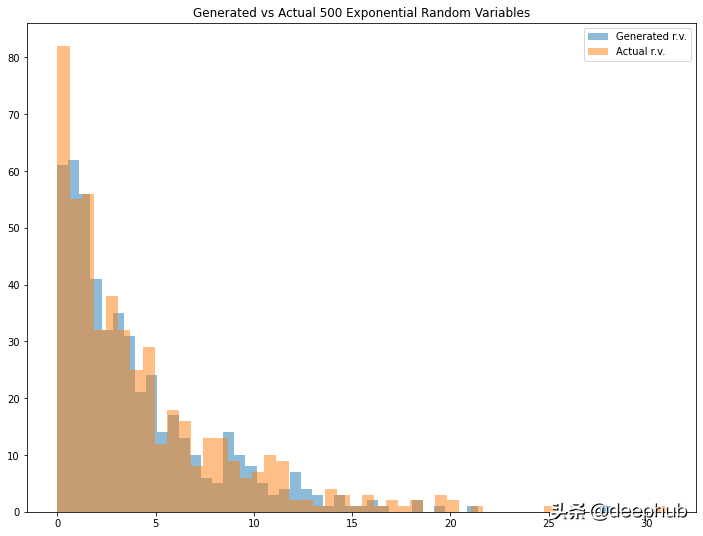
在Python中使用逆变换方法生成随机变量

看起来很有趣。如果将其与实际变量进行比较，我们可以看到生成的随机变量具有非常相似的结果。可以调整均值(请注意，我为expon.rvs()函数定义的均值是指数分布中的比例参数)和/或生成的随机变量的数量，以查看不同的结果。

离散随机数实现代码

对于离散随机变量情况，假设我们要模拟遵循以下分布的离散随机变量情况X

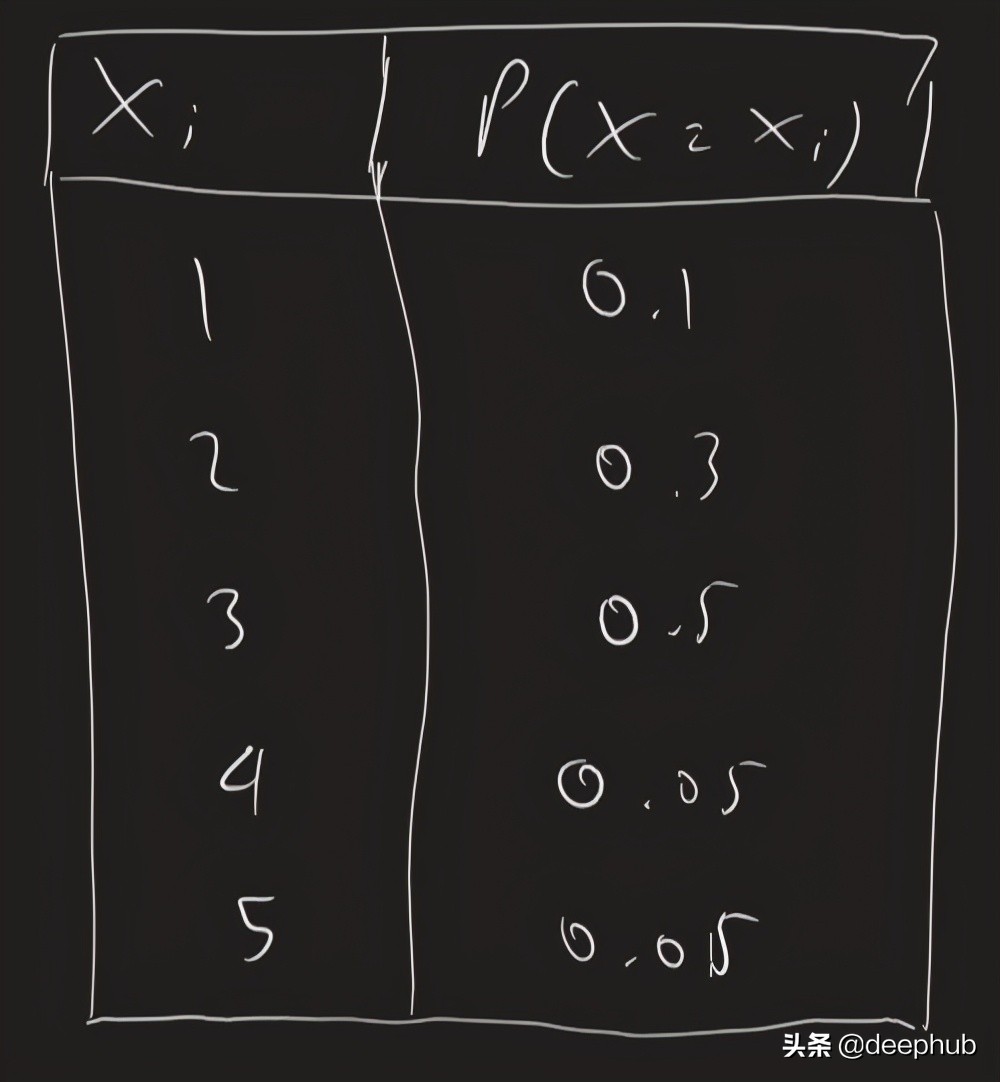
首先，我们编写函数以使用这些代码行为一个样本生成离散随机变量。

### Generate arbitary discrete distributed random variables given  
### the probability vector  
def discrete_inverse_trans(prob_vec):  
U=uniform.rvs(size=1)  
if U<=prob_vec[0]:  
return 1  
else:  
for i in range(1,len(prob_vec)+1):  
if sum(prob_vec[0:i])<U and sum(prob_vec[0:i+1])>U:  
return i+1

然后，我们创建一个函数以使用这些代码行生成许多随机变量样本。

def discrete_samples(prob_vec,n=1):  
sample=[]  
for i in range(0,n):  
sample.append(discrete_inverse_trans(prob_vec))  
return np.array(sample)

最后，我们创建一个函数来模拟结果，并通过这些代码行将其与实际结果进行比较。

def discrete_simulate(prob_vec,numbers,n=1):  
sample_disc=discrete_samples(prob_vec,n)  
unique, counts=np.unique(sample_disc,return_counts=True)  
 
fig=plt.figure()  
ax=fig.add_axes([0,0,1,1])  
prob=counts/n  
ax.bar(numbers,prob)  
ax.set_title("Simulation of Generating %i Discrete Random Variables" %n)  
plt.show()  
 
data={'X':unique,'Number of samples':counts,'Empirical Probability':prob,'Actual Probability':prob_vec}  
df=pd.DataFrame(data=data)  
return df

我们可以在下面运行一些示例以查看结果。同样，请注意，由于我们要生成随机变量，因此结果可能会有所不同。

prob_vec=np.array([0.1,0.3,0.5,0.05,0.05])  
numbers=np.array([1,2,3,4,5])  
 
dis_example1=discrete_simulate(prob_vec, numbers, n=100)  
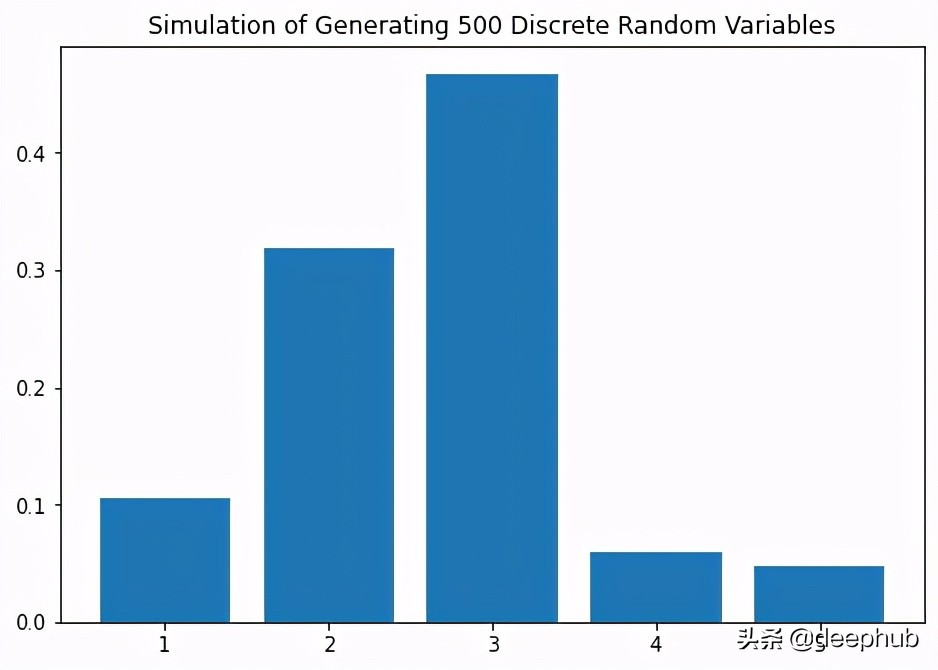
dis_example2=discrete_simulate(prob_vec, numbers, n=500)  
dis_example3=discrete_simulate(prob_vec, numbers, n=1000)

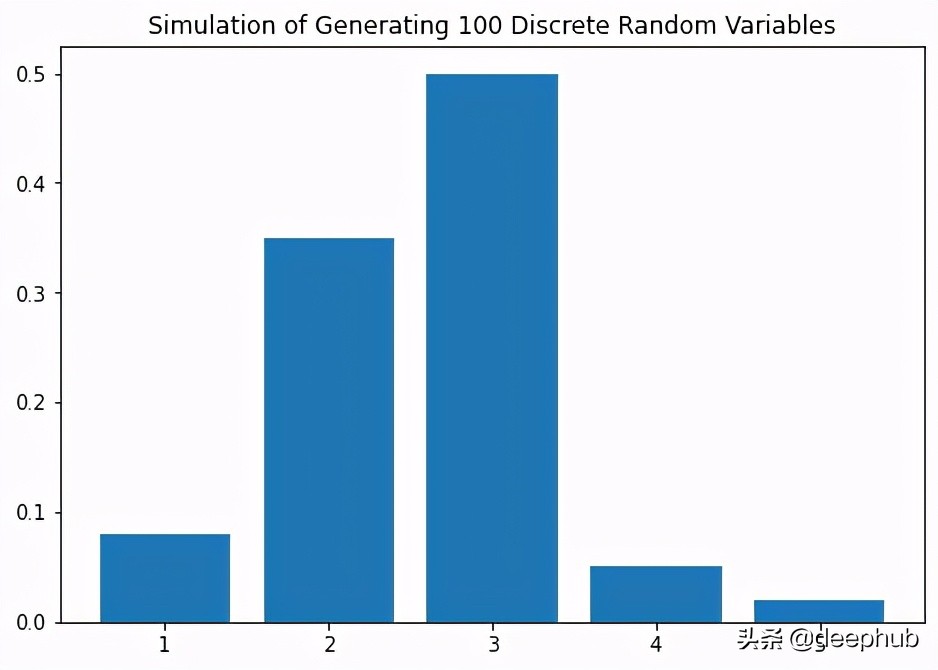
在Python中使用逆变换方法生成随机变量

In[11]: dis_example1  
Out[11]:  
X Number of samples Empirical Probability Actual Probability  
0 1 8 0.08 0.10  
1 2 35 0.35 0.30  
2 3 50 0.50 0.50  
3 4 5 0.05 0.05  
4 5 2 0.02 0.05In[12]: dis_example2  
Out[12]:  
X Number of samples Empirical Probability Actual Probability  
0 1 53 0.106 0.10  
1 2 159 0.318 0.30  
2 3 234 0.468 0.50  
3 4 30 0.060 0.05  
4 5 24 0.048 0.05In[13]: dis_example3  
Out[13]:  
X Number of samples Empirical Probability Actual Probability  
0 1 108 0.108 0.10  
1 2 290 0.290 0.30  
2 3 491 0.491 0.50  
3 4 51 0.051 0.05  
4 5 60 0.060 0.05

结果很有趣! 我们可以看到，随着我们增加随机变量样本的数量，经验概率越来越接近实际概率。尝试使用不同数量的样本和/或不同的分布进行实验，以查看不同的结果。

总结

这种逆变换方法是统计中非常重要的工具，尤其是在仿真理论中，在给定随机变量均匀分布在(0,1)中的情况下，我们想生成随机变量。研究案例本身非常广泛，您可以使用在生成经验累积分布函数，预测分析中使用到的这种方法。