两个框架的故事：pytorch与tensorflow

使用Pytorch 1.x和Tensorflow 2.x比较自动差异和动态模型子类方法

> Source: Author

数据科学界是一种充满活力和合作的空间。我们从彼此的出版物中学到，辩论关于论坛和在线网点的想法，并分享许多代码(和许多)代码。这种合作精神的自然副作用是遇到同事使用的不熟悉工具的高可能性。因为我们不在真空中工作，所以在给定的主题领域中获得熟悉多种语言和图书馆的熟悉程度往往是有意义的，以便合作和学习最有效。

这并不奇怪，那么，许多数据科学家和机器学习工程师在其工具箱中有两个流行的机器学习框架：Tensorflow和Pytorch。这些框架 - 在Python中 - 分享许多相似之处，也以有意义的方式分歧。这些差异，例如它们如何处理API，加载数据和支持专业域，可以在两个框架繁琐且效率低下之间交替。这是一个问题，给出了这两个工具的常见。

因此，本文旨在通过专注于创建和训练两个简单模型的基础知识来说明Pytorch和Tensorflow之间的差异。特别是，我们将介绍如何使用来自Pytorch 1.x的模块API和来自Tensorflow 2.x的模块API使用动态子类模型。我们将查看这些框架的自动差异如何，以提供非常朴素的梯度下降的实现。

但首先，数据

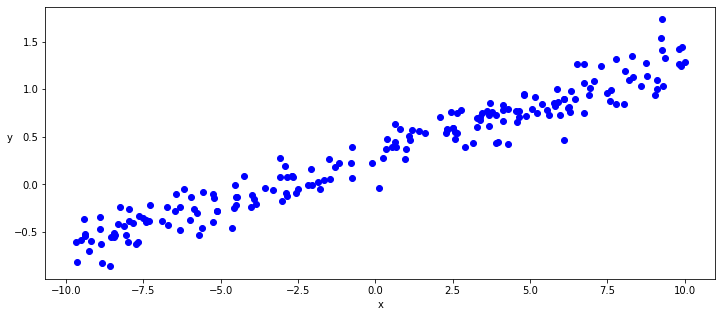
因为我们专注于自动差分/自动求导功能的核心(作为一种进修，是可以自动提取函数的导数的容量并在一些参数上应用梯度，以便使用这些参数梯度下降)我们可以从最简单的模型开始，是线性回归。我们可以使用Numpy库使用一点随机噪声生成一些线性数据，然后在该虚拟数据集上运行我们的模型。

def generate_data(m=0.1, b=0.3, n=200): 
  x = np.random.uniform(-10, 10, n) 
  noise = np.random.normal(0, 0.15, n) 
  y = (m * x + b ) + noise 
  return x.astype(np.float32), y.astype(np.float32) 
x, y = generate_data() 
plt.figure(figsize = (12,5)) 
ax = plt.subplot(111) 
ax.scatter(x,y, c = "b", label="samples") 

模型

一旦我们拥有数据，我们就可以从Tensorflow和Pytorch中的原始代码实现回归模型。为简单起见，我们不会最初使用任何层或激活器，仅定义两个张量，W和B，表示线性模型Y = Wx + B的权重和偏置。

正如您所看到的，除了API名称的几个差异之外，两个模型的类定义几乎相同。最重要的区别在于，Pytorch需要一个明确的参数对象来定义由图捕获的权重和偏置张量，而TensoRFlow能够自动捕获相同的参数。实际上，Pytorch参数是与模块API一起使用时具有特殊属性的Tensor子类：它们会自动向模块参数列表添加SELF，因此SECRES在参数()迭代器中出现。

这两个框架都提取了从此类定义和执行方法生成图所需的一切(__call__或转发)，并且如下，如下所示，计算实现bospropagation所需的渐变。

Tensorflow动态模型

class LinearRegressionKeras(tf.keras.Model): 
  def __init__(self): 
    super().__init__() 
    self.w = tf.Variable(tf.random.uniform(shape=[1], -0.1, 0.1)) 
    self.b = tf.Variable(tf.random.uniform(shape=[1], -0.1, 0.1)) 
     
  def __call__(self,x):  
    return x * self.w + self.b 

Pytorch动态模型

class LinearRegressionPyTorch(torch.nn.Module):  
  def __init__(self):  
    super().__init__()  
    self.w = torch.nn.Parameter(torch.Tensor(1, 1).uniform_(-0.1, 0.1)) 
    self.b = torch.nn.Parameter(torch.Tensor(1).uniform_(-0.1, 0.1)) 
   
  def forward(self, x):   
    return x @ self.w + self.b 

构建训练循环，backpropagation和优化器

使用这些简单的Tensorflow和Bytorch模型建立，下一步是实现损失函数，在这种情况下只是意味着平方错误。然后，我们可以实例化模型类并运行训练循环以实现几个周期。

同样，由于我们专注于核心自动差分/自动求导功能，这里的目的是使用TensorFlow和特定于Pytorch特定的自动Diff实现构建自定义训练循环。这些实施方式计算简单的线性函数的梯度，并用天真梯度下降优化器手动优化权重和偏置参数，基本上最小化了在每个点处使用可微差函数之间计算的实际点和预测之间计算的损失。

对于TensorFlow训练循环，我明确地使用GradientTape API来跟踪模型的前向执行和逐步损耗计算。我使用GradientTape的渐变来优化权重和偏置参数。Pytorch提供了一种更“神奇的”自动求导方法，隐式地捕获参数张量的任何操作，并提供用于优化权重和偏置参数的梯度，而无需调用另一API。一旦我具有权重和偏置梯度，在Pytorch和Tensorflow上实现自定义梯度下降方法就像从这些梯度中减去权重和偏置参数一样简单，乘以恒定的学习速率。

请注意，由于Pytorch自动实现自动差分/自动求导，因此在计算后向传播之后，有必要明确调用no_grad api。这指示Pytorch不计算权重和偏置参数的更新操作的梯度。我们还需要明确释放在前向操作中计算的先前自动计算的渐变，以阻止Pytorch自动累积较批次和循环迭代中的渐变。

Tensorflow训练循环

def squared_error(y_pred, y_true): 
  return tf.reduce_mean(tf.square(y_pred - y_true)) 
 
tf_model = LinearRegressionKeras() 
[w, b] = tf_model.trainable_variables 
 
for epoch in range(epochs): 
  with tf.GradientTape() as tape: 
    predictions = tf_model(x) 
    loss = squared_error(predictions, y) 
         
  w_grad, b_grad = tape.gradient(loss, tf_model.trainable_variables) 
  w.assign(w - w_grad * learning_rate) 
  b.assign(b - b_grad * learning_rate) 
 
  if epoch % 20 == 0: 
    print(f"Epoch {epoch} : Loss {loss.numpy()}") 

Pytorch训练循环

def squared_error(y_pred, y_true): 
  return torch.mean(torch.square(y_pred - y_true)) 
 
torch_model = LinearRegressionPyTorch() 
[w, b] = torch_model.parameters() 
 
for epoch in range(epochs): 
  y_pred = torch_model(inputs) 
  loss = squared_error(y_pred, labels) 
  loss.backward() 
   
  with torch.no_grad(): 
    w -= w.grad * learning_rate 
    b -= b.grad * learning_rate 
    w.grad.zero_() 
    b.grad.zero_() 
     
  if epoch % 20 == 0: 
    print(f"Epoch {epoch} : Loss {loss.data}") 

Pytorch和Tensorflow模型重用可用层

既然我展示了如何从Pytorch和Tensorflow中的原始代码实现线性回归模型，我们可以查看如何使用密集和线性层，从TensorFlow和Pytorch库中重新实现相同的型号。

带现有图层的TensoRFlow和Pytorch动态模型

您将在模型初始化方法中注意到，我们正在用TensorFlow中的密集层替换W和B参数的显式声明和Pytorch中的线性层。这两个层都实现了线性回归，并且我们将指示它们使用单个权重和偏置参数来代替以前使用的显式W和B参数。密集和线性实现将在内部使用我们之前使用的相同的张解声明(分别为tf.variable和nn.parameter)来分配这些张量并将它们与模型参数列表相关联。

我们还将更新这些新模型类的呼叫/前进方法，以替换具有密度/线性层的手动线性回归计算。

class LinearRegressionKeras(tf.keras.Model): 
    def __init__(self): 
        super().__init__() 
        self.linear = tf.keras.layers.Dense(1, activation=None) # , input_shape=[1] 
 
    def call(self, x):  
        return self.linear(x) 

class LinearRegressionPyTorch(torch.nn.Module): 
    def __init__(self): 
        super(LinearRegressionPyTorch, self).__init__() 
        self.linear = torch.nn.Linear(1, 1)   
 
    def forward(self, x): 
        return self.linear(x) 

具有可用优化器和损耗函数的训练

既然我们已经使用现有图层重新实现了我们的Tensorflow和Pytorch型号，我们可以专注于如何构建更优化的训练循环。我们不是使用我们以前的Naïve实现，我们将使用这些库可用的本机优化器和损失函数。

我们将继续使用之前观察到的自动差分/自动求导功能，但此时具有标准渐变下降(SGD)优化实现以及标准损耗功能。

Tensorflow训练循环，易于拟合方法

在Tensorflow中，FIT()是一种非常强大，高级别的训练模型方法。它允许我们用单个方法替换手动训练循环，该方法指定超级调整参数。在调用fit()之前，我们将使用Compile()方法编译模型类，然后通过梯度后代优化器和用于训练的损失函数。

您会注意到在这种情况下，我们将尽可能多地重用来自TensorFlow库的方法。特别是，我们将通过标准随机梯度下降(SGD)优化器和标准的平均绝对误差函数实现(MEAL_ABSOLUTE_ERROR)到编译方法。一旦模型进行编译，我们最终可以拨打拟合方法来完全训练我们的模型。我们将通过数据(x和y)，epochs的数量以及每个时代使用的批量大小。

带有自定义循环和SGD优化器的TensoRFLOF训练循环

在以下代码段中，我们将为我们的模型实施另一个自定义训练循环，这次尽可能多地重用由Tensorflow库提供的损失函数和优化器。您会注意到我们的前自定义Python损失函数替换为tf.losses.mse()方法。我们初始化了TF.keras.optimizers.sgd()优化程序而不是用渐变手动更新模型参数。调用Optimizer.apply_gradient()并传递权重和偏置元组列表将使用渐变更新模型参数。

tf_model_train_loop = LinearRegressionKeras() 
 
optimizer = tf.keras.optimizers.SGD(learning_ratelearning_rate=learning_rate) 
 
for epoch in range(epochs * 3): 
    x_batch = tf.reshape(x, [200, 1]) 
    with tf.GradientTape() as tape: 
        y_pred = tf_model_train_loop(x_batch) 
        y_pred = tf.reshape(y_pred, [200]) 
        loss = tf.losses.mse(y_pred, y) 
     
    grads = tape.gradient(loss, tf_model_train_loop.variables) 
     
    optimizer.apply_gradients(grads_and_vars=zip(grads, tf_model_train_loop.variables)) 
 
    if epoch % 20 == 0: 
        print(f"Epoch {epoch} : Loss {loss.numpy()}") 

具有自定义循环和SGD优化器的Pytorch训练循环

与上面的上一个Tensorflow代码段一样，以下代码片段通过重用Pytorch库提供的丢失功能和优化器来实现新模型的Pytorch训练循环。您会注意到我们将使用NN.Mseloss()方法替换我们以前的自定义Python丢失函数，并初始化标准Optim.sgd()优化程序，其中包含模型的学习参数列表。如前所述，我们将指示Pytorch从丢失向后传播中获取每个参数张量的关联梯度(load.backward())，最后，我们可以通过调用来容易地更新新标准优化器与与梯度相关联的所有参数更新新的标准优化器优化器.step()方法。Pytorch使张量和梯度之间自动关联的方式允许优化器检索张量和梯度以通过配置的学习速率更新它们。

torch_model = LinearRegressionPyTorch() 
 
criterion = torch.nn.MSELoss(reduction='mean') 
optimizer = torch.optim.SGD(torch_model.parameters(), lr=learning_rate) 
 
for epoch in range(epochs * 3): 
    y_pred = torch_model(inputs) 
    loss = criterion(y_pred, labels) 
    optimizer.zero_grad() 
    loss.backward() 
    optimizer.step() 
 
    if epoch % 20 == 0: 
      print(f"Epoch {epoch} : Loss {loss.data}") 

结果

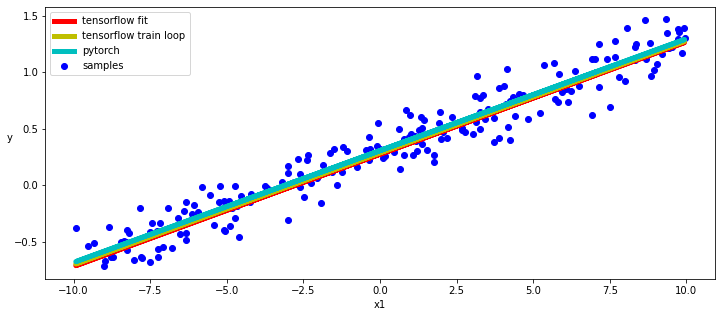
正如我们所看到的那样，TensoRFlow和Pytorch自动差分和动态子类API非常相似，即使它们使用标准SGD和MSE实现方式也是如此。当然，这两个模型也给了我们非常相似的结果。

在下面的代码片段中，我们使用Tensorflow的Training_variables和Pytorch的参数方法来获得对模型的参数的访问，并绘制我们学习的线性函数的图表。

[w_tf, b_tf] = tf_model_fit.trainable_variables 
[w2_tf, b2_tf] = tf_model_train_loop.trainable_variables 
[w_torch, b_torch] = torch_model.parameters() 
 
w_tf = tf.reshape(w_tf, [1]) 
w2_tf = tf.reshape(w2_tf, [1]) 
 
with torch.no_grad(): 
  plt.figure(figsize = (12,5)) 
  ax = plt.subplot(111) 
  ax.scatter(x, y, c = "b", label="samples") 
  ax.plot(x, w_tf * x + b_tf, "r", linewidth = 5.0, label = "tensorflow fit") 
  ax.plot(x, w2_tf * x + b2_tf, "y", linewidth = 5.0, label = "tensorflow train loop") 
  ax.plot(x, w_torch * inputs + b_torch, "c", linewidth = 5.0, label = "pytorch") 
  ax.legend() 
  plt.xlabel("x1") 
  plt.ylabel("y",rotation = 0) 

结论

Pytorch和新Tensorflow 2.x都支持动态图形和自动差分核心功能，以提取图表中使用的所有参数的渐变。您可以轻松地在Python中实现训练循环，其中包含任何损失函数和渐变后代优化器。为了专注于两个框架之间的真实核心差异，我们通过实施自己的简单MSE和NaïveSGD来简化上面的示例。

但是，我强烈建议您在实现任何Naïve代码之前重用这些库上可用的优化和专用代码。

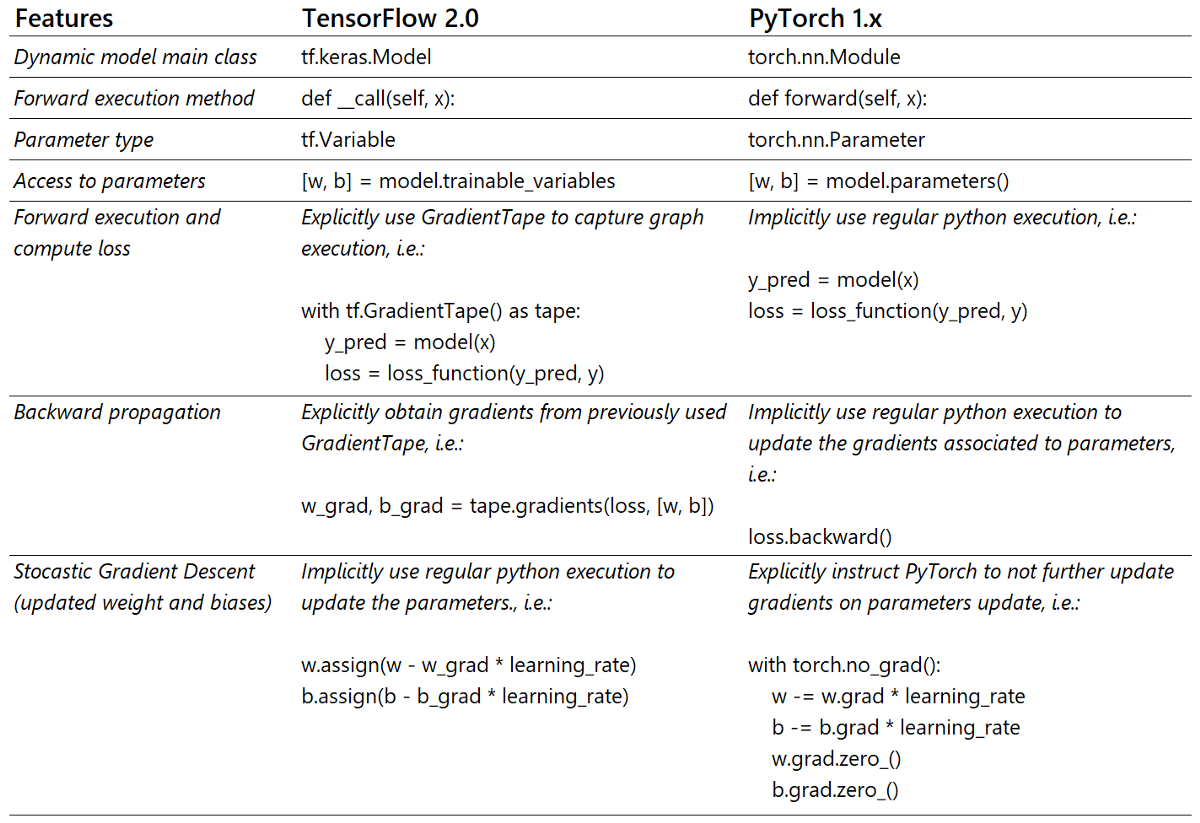
下表总结了上面示例代码中所注明的所有差异。我希望它可以作为在这两个框架之间切换时的有用参考。

> Source: Author

原文链接：

https://medium.com/data-science-at-microsoft/a-tale-of-two-frameworks-pytorch-vs-tensorflow-f73a975e733d