前言
今天说说二叉树。
树
首先看看什么是树??。
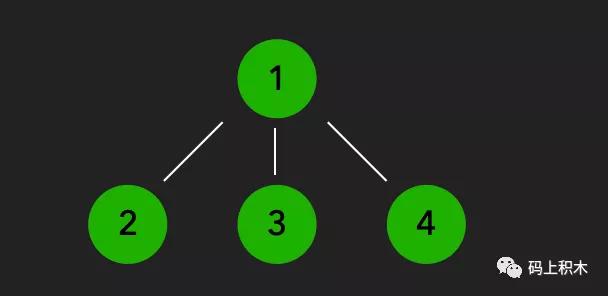
如图,这种有节点的结构就是树。
树 是n(n>=0)个结点的有限集
其中:
- 每个元素叫做 节点
- 上一节是下一节的 父节点,比如1是2的父节点
- 最上面的节点,也就是没有父节点的节点叫做 根节点,比如1
- 同一个父节点的节点叫做 兄弟节点,比如2、3、4是兄弟节点
- 没有子节点的节点叫做 叶子节点
二叉树
听名字还是比较好理解的,就是每个节点有两个分叉的树。但是又不要求一定有两个节点,只要小于等于2个节点就可以。
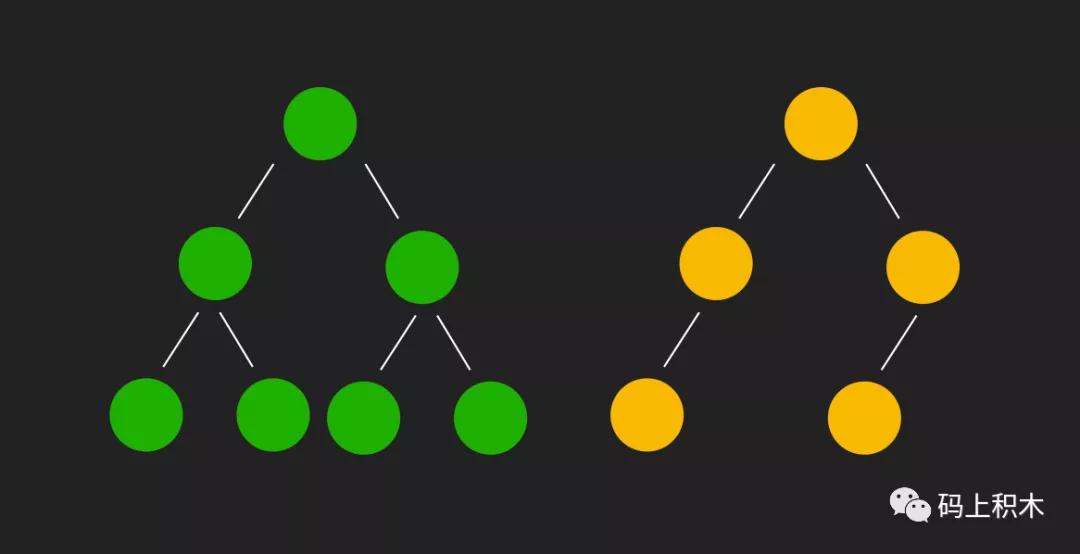
比如这种:
其中,可以看到绿色的树每个节点都有左右两个节点,这种二叉树就叫做 满二叉树。
还有一种二叉树叫做 完全二叉树。
完全二叉树: 对一颗具有n个结点的二叉树按层编号,如果编号为i(1<=i<=n)的结点与同样深度的满二叉树中编号为i的结点在二叉树中位置完全相同,则这棵二叉树称为完全二叉树。
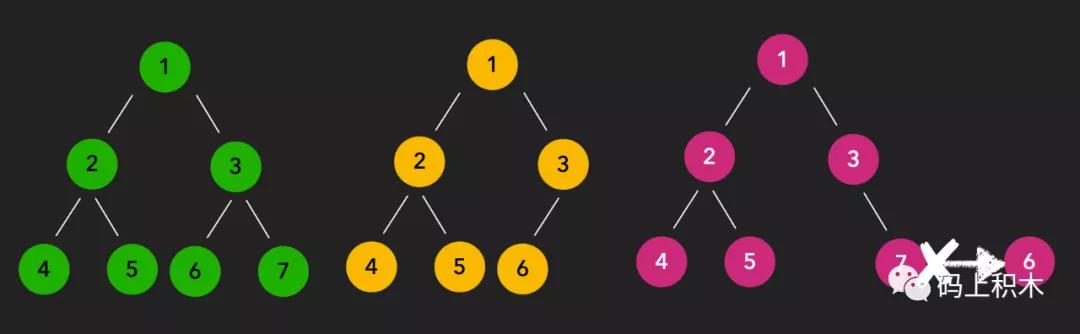
啥意思呢,比如一个满二叉树,每个节点进行顺序编号,如果去了一些节点,编号不会变化,那么就是完全二叉树,比如:
这张图中,绿色树是满二叉树,当去掉7号节点,变成了黄色树。
这颗黄色树的序号相对于满二叉树的序号都能一一对应,所以这个黄色树就是完全二叉树。
如果去掉的是6号节点,变成红色树,这时候,红色树的节点就必须有所变化了,6消失后节点7必须变成节点6才正确。
所以这个红色树就不是完全二叉树,因为它相对于满二叉树序号有所改变,已经对应不上了。
算法——平衡二叉树
说了这么多,该来个题练练手了。
输入一棵二叉树的根节点,判断该树是不是平衡二叉树。如果某二叉树中任意节点的左右子树的深度相差不超过1,那么它就是一棵平衡二叉树。
示例 1: 给定二叉树 [3,9,20,null,null,15,7]
3
/ \
9 20
/ \
15 7
- 1.
- 2.
- 3.
- 4.
- 5.
返回 true 。
解析
题目给出了平衡二叉树的概念,就是任意节点的左右子树相差不超过1,就是平衡二叉树。
那这个深度是啥呢?
深度就是根节点到当前节点经过的边个数
层数就是当前节点在第几层,跟节点为第一层,所以层数=深度+1
1 深度 0 ,层数 1
/ \
2 3 深度 1 ,层数 2
/ \
4 5 深度 2 ,层数 3
- 1.
- 2.
- 3.
- 4.
- 5.
解法1
首先容易想到的就是把每个节点的深度都算出来,然后进行左右节点比较就能得出是不是平衡二叉树。
那么节点的子树深度怎么计算呢?
递归。当子节点为空就返回,否则每次增加一个单位深度。
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
private int depth(TreeNode root) {
if (root == null) return 0;
return Math.max(depth(root.left), depth(root.right)) + 1;
}
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
深度搞定了,这题就好解了,即遍历每个节点的左右深度,还是要 用到递归:
class Solution {
public boolean isBalanced(TreeNode root) {
if (root == null) return true;
return Math.abs(depth(root.left) - depth(root.right)) <= 1 && isBalanced(root.left) && isBalanced(root.right);
}
private int depth(TreeNode root) {
if (root == null) return 0;
return Math.max(depth(root.left), depth(root.right)) + 1;
}
}
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
从根节点开始,计算每个左子树深度和右子树深度的差值,以及下面的每个节点的左子树和右子树深度,最终得出结果。
这种先处理节点,在处理左子树,再处理右子树 的遍历方式叫做 前序遍历或者先序遍历。
时间复杂度
假设节点总数为n,层数为x,二叉树为满二叉树。
时间复杂度计算可以通过 每层的时间复杂度 * 层数复杂度
每层的时间复杂度:
- 第一层需要遍历n次,第二层需要遍历n-1次,第三层需要遍历n-3次,所以每层的时间复杂度为O(n)
层数复杂度:
- 第一层为1个节点,第二层为2个节点,第三层为4个节点,第x层为2的x-1次方。
借助公式:
n >= 1+2+4+8+...+2^(x-2)+1
n <= 1+2+4+8+...+2^(L-2)+2^(L-1)
- 1.
- 2.
计算:
n >= 1+2+4+8+...+2^(x-2)+1
n >= (2^(x-1)-1) + 1
n >= 2^(x-1)
x <= log2n+1
- 1.
- 2.
- 3.
- 4.
同理:
x >= log2(n+1)
- 1.
所以一个接近平衡二叉树的高度(层数)接近logn。
所以总的时间复杂度就是 O(nlogn)
空间复杂度
由于用到了递归,用到了堆栈帧,之前说过和最大递归深度成正比,所以空间复杂度为O(n)
解法2
还有没有更好的解呢?
刚才我们用到的是先序遍历,但是可以发现,每个节点都会计算一遍深度,会有大量重复计算,所以我们可以试试不重复的算法?比如直接后序遍历。
后序遍历:对于任意节点来说,先处理左子树,再处理右子树,最后再处理节点本身。
计算深度还是用到刚才的方法:
private int depth(TreeNode root) {
if (root == null) return 0;
int left = recur(root.left);
int right = recur(root.right);
return Math.max(left, right) + 1;
}
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
如果能计算左子树深度和右子树深度,那么我们可以直接进行比较,如果发现某个节点的左子树深度和右子树深度相差大于1,那么就可以直接返回false了。
所以综合能得出解法二:
class Solution {
public boolean isBalanced(TreeNode root) {
return recur(root) != -1;
}
private int recur(TreeNode root) {
if (root == null) return 0;
int left = recur(root.left);
if(left == -1) return -1;
int right = recur(root.right);
if(right == -1) return -1;
return Math.abs(left - right) < 2 ? Math.max(left, right) + 1 : -1;
}
}
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
时间复杂度
n为总节点,遍历所有节点,所以时间复杂度为O(n)
空间复杂度
O(n)
- 1.
参考
https://leetcode-cn.com/problems/ping-heng-er-cha-shu-lcof/
https://time.geekbang.org/column/article/67856
本文转载自微信公众号「码上积木」,可以通过以下二维码关注。转载本文请联系码上积木公众号。