3 月 12 号,是全国的重大节日:植树节。记得小时候就跟随老师一起植过树。现在参加工作了,虽然没有植过树,但是学到过很多树的结构,比如二叉树、B+ 树,红黑树。每次面试必问,恰逢植树节,本来是想讲解 B 树,但发现必须要理解了二叉树之后才能更好地讲解 B 树,所以先给大家讲下二叉树是什么,后面文章再更新 B 树。
大白话讲解二叉树
比如现在有个数组,存放了很多用户的名字,需要从这个数组中找到包含指定的用户名,最快的方式是什么?
我们会想到二分查找,虽然这种方式很快,但要达到最快还需要有个条件:数组有序。
如果我们能把插入用户名的时候直接给他排序,那最后的结构就是有序结构。
因此有人设计了一种数据结构:二叉查找树,也叫做二叉树。
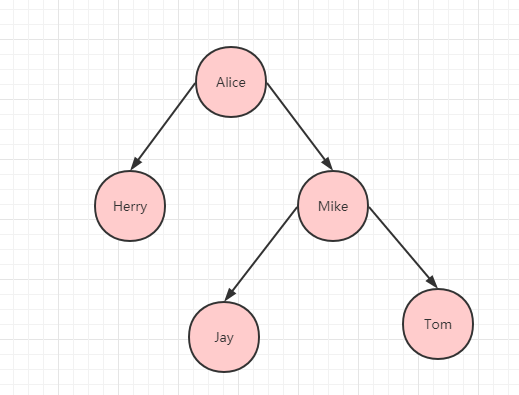
如下图所示:这是一种二叉树结构。
二叉树
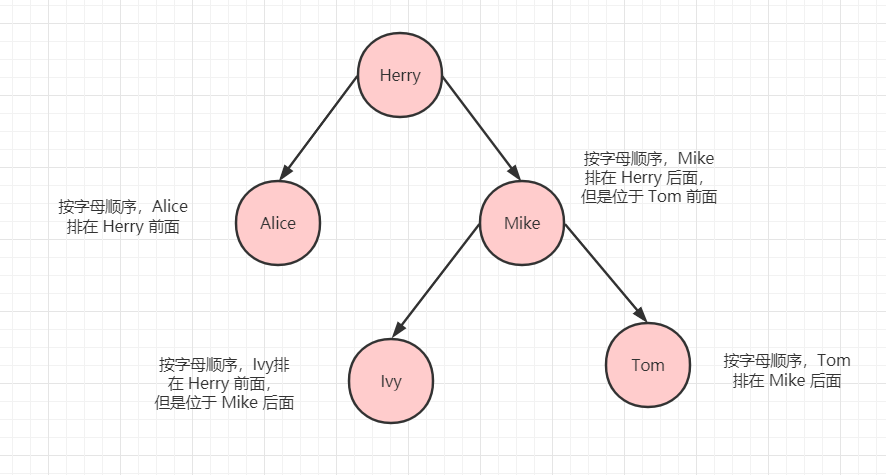
根据上文中的例子的,假定 Herry 在最上面,下面有 Alice,Mike,Ivy,Tom,从左到右,从上到下来看的话,最后的排序是:Alice->Herry->Ivy->Mike->Tom,确实是按照字母顺序排的。
名字排序说明
其中有四个术语需要说明:节点、左节点、右节点、根节点。
其中每个红色圆球都算一个节点,节点左下边相连接的节点叫做左节点,而右边相连的叫做右节点。比如 Alice 被称作 Herry 节点的左节点,Mike 被称作 Herry 的右节点。而根节点只会有一个,属于最上面的节点,上图中的 Herry 就是根节点。
对于其中每个节点,左子节点的值都比它小,而右子节点的值都比它大。比如 Alice < Herry < Mike。
假设现在我们想要查找 Ivy,首先检查根节点,发现比 Herry 大,所以往下继续找,找到了根节点的右节点 Mike,再继续找,比 Mike 小,所以找 Mike 的左节点,正好找到 Ivy。
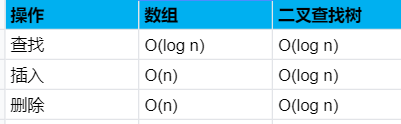
二叉查找树中查找节点时,平均运行时间是 O(logn),最糟糕的情况下所需时间为 O(n); 而在有序数组中查找时,及时最糟糕的情况,二分查找最多也是 O(logn),所以你可能会觉得,二分查找比二叉查找要快很多。但是二叉查找树的插入和删除操作的速度是要快很多的。这里我们做一个对比:
二叉树与二分查找算法对比
但是二叉树也有缺点:
- 不能随机访问。比如想要查找第 10 个元素,是不能返回第十个元素的,但是数组就可以通过下标索引找到。
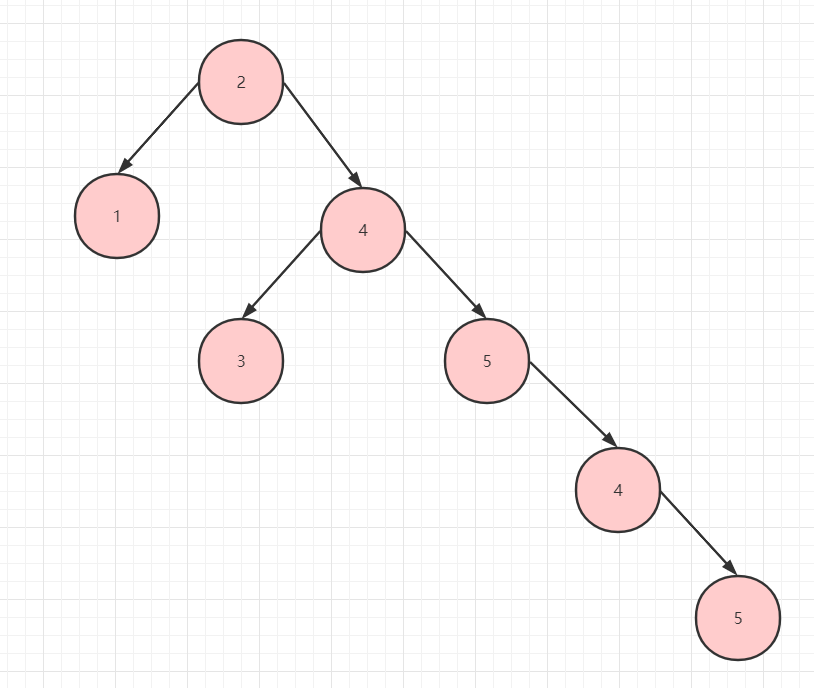
- 二叉树存在不平衡的情况,比如以根节点为中间的界限,发现右边的节点数远超左边的节点数,那么左右不平衡,查找的效率就很低了。如下图所示:
右边节点数远大于左边节点数
那有没有平衡的二叉树呢?当然有,那就是红黑树,限于篇幅和侧重点,这个放到下篇再讲吧
二叉树中的含义
二叉树定义
大白话说二叉树就是每个节点只能有两颗子树,且有左右之分。
来看看专业定义:二叉树是 n(n>=0 ) 个结点的有限集合,该集合或者为空集(称为空二叉树),或者由一个根结点和两棵互不相交的、分别称为根结点的左子树和右子树组成。
二叉树有 5 种形态
空二叉树。
只有一个根节点的二叉树。
只有左子树
只有右子树。
完全二叉树。
节点的度
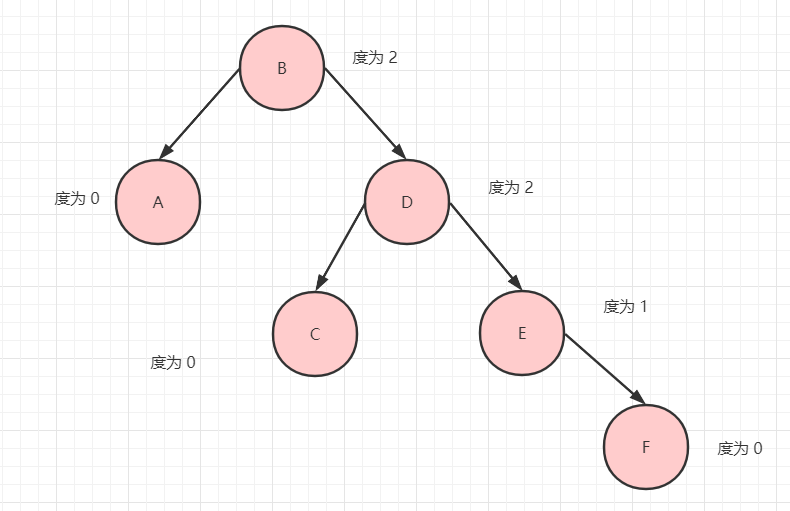
定义:节点拥有的子树数目称为节点的度。
我们来看下图就一目了然了。
mark
比如节点 B 的度为 2,节点 E 的度 为 1.
而树的度就是所有节点的度的最大值,也就是 2。
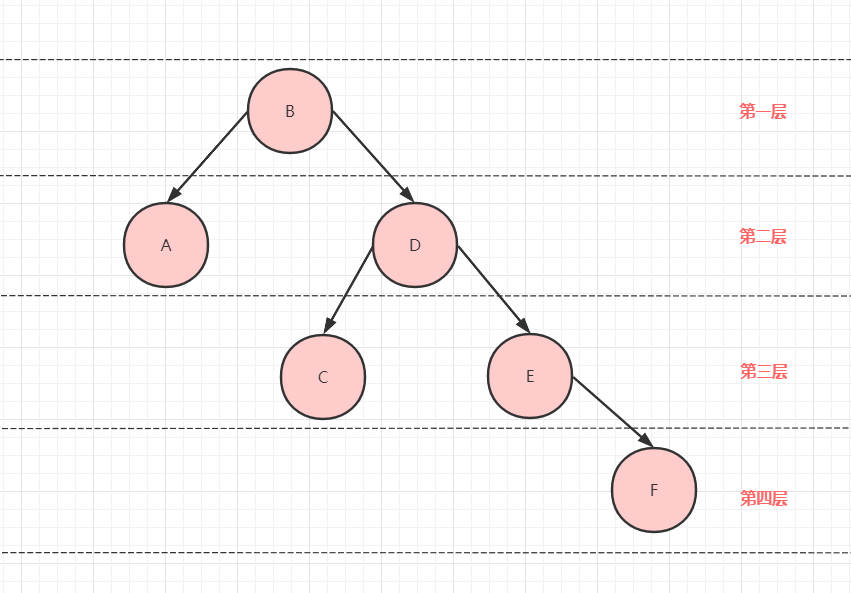
节点层次
如下图所示:根节点为第一层,依次类推。
二叉树的特点
每个节点最多有颗子树,所以二叉树中不存在度大于 2 的节点。
左右子树是有顺序的,次序不能任意颠倒。
即使某个节点只有一颗子树,也是需要区分它是左子树还是右子树。
二叉树的遍历
二叉树的遍历:从二叉树的根节点出发,按照某种次序依次访问二叉树中的所有节点,使得每个节点都能被访问一次,且仅被访问一次。
二叉树的访问次序可以分为四种:
- 前序遍历。
- 中序遍历。
- 后续遍历。
- 层序遍历。
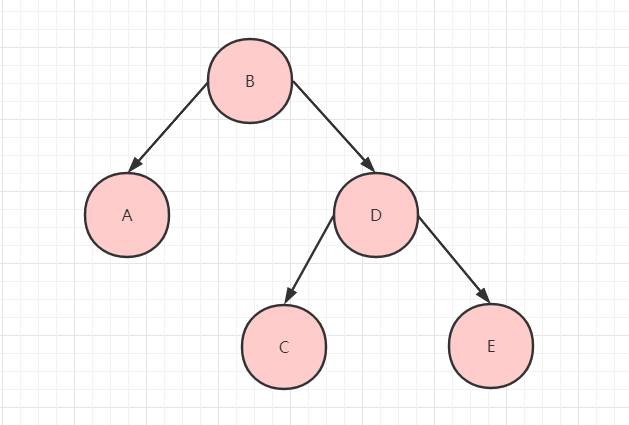
前序遍历:通俗的说就是从二叉树的根结点出发,当第一次到达结点时就输出结点数据,按照先向左再向右的方向访问。
中序遍历:就是从二叉树的根结点出发,当第二次到达结点时就输出结点数据,按照先向左再向右的方向访问。
后序遍历:就是从二叉树的根结点出发,当第三次到达结点时就输出结点数据,按照先向左再向右的方向访问。
层次遍历:就是按照树的层次自上而下的遍历二叉树。
mark
按照前序遍历的结果就是 BADCE。
按照中序遍历的结果就是 ABCDE。
按照后续遍历的结果就是 ACEDB。
按照层次遍历的结果就是 BADCE。
巨人的肩膀:
《算法图解》
本文转载自微信公众号「悟空聊架构」,可以通过以下二维码关注。转载本文请联系悟空聊架构公众号。