Python被确定为数据科学和机器学习的进入语言,部分感谢开源ML库Pytorch。
Pytorch的功能强大的深度神经网络建筑工具和易用性使其成为数据科学家的热门选择。随着其人气的发展,越来越多的公司正在从Tensorflow转移到Pytorch,现在开始使用Pytorch的最佳时间。
今天,我们将帮助了解Pytorch如此流行的是什么,使用Pytorch的一些基础,并帮助您制作第一个计算模型。
什么是pytorch?
PyTorch是一个开源机器学习Python库,用于深度学习实现,如计算机视觉(使用武器)和自然语言处理。它是由Facebook的AI Research Lab(Fair)于2016年开发的,自数据科学和ML领域以来已采用。
Pytorch为已经熟悉Python的人提供了直观的机器,并且具有oop支持和动态计算图等具有很大的功能。
除了构建深度神经网络之外,由于其GPU加速,Pytorch也非常适合复杂的数学计算。此功能允许Pytorch使用计算机的GPU来大量加速计算。
这种独特的功能和Pytorch的无与伦比的简单的组合使其成为最受欢迎的深度学习库之一,只有顶点的Tensorflow竞争。
为什么要使用pytorch?
在Pytorch之前,开发人员使用高级微积分来查找反向传播错误和节点加权之间的关系。更深的神经网络呼吁越来越复杂的操作,限制机器学习的规模和易在性。
现在,我们可以使用ML图书馆自动完成所有的微积分!ML库可以在几秒钟内计算任何大小或形状网络,允许更多开发人员构建更大和更好的网络。
Pytorch通过表现类似于标准Python来进一步逐步迈出此访问。您可以使用现有的Python知识来快速开始启动现有的Python知识而不是学习新的语法。此外,您可以使用Pytorch使用额外的Python库,例如Pycharm调试器等流行调试器。
pytorch与tensorflow.
Pytorch和Tensorflow之间的主要区别是简单和性能之间的权衡:Pytorch更容易学习(特别是对于Python程序员),而Tensorflow具有学习曲线,但执行更好并且更广泛地使用。
- 人气:Tensorflow是行业专业人士和研究人员的当前转向工具,因为它比Pytorch较早发布了1年。然而,Pytorch用户的速度比Tensorflow更快,表明Pytorch可能很快是最受欢迎的。
- 数据并行性:Pytorch包括声明性数据并行性,换句话说,它会自动将数据处理的工作量分布在不同的GPU上以加速性能。Tensorflow有并行性,但它要求您手动分配工作,这通常是耗时和更少的效率。
- 动态与静态图表:Pytorch默认情况下具有动态图形,可立即响应新数据。Tensorflow使用TensoRFlow Fold对动态图形的支持有限,但主要使用静态图形。
- 集成:由于其通过武器密切连接,Pytorch适用于AWS上的项目。Tensorflow与Google Cloud相结合,并且由于其使用SWIFT API而非常适合移动应用程序。
- 可视化:Tensorflow拥有更强大的可视化工具,并提供更精细的图形设置控制。Pytorch的愿望可视化工具或类似Matplotlib的其他标准绘图库并不像Tensorflow那样完全齐全,但它们更容易学习。
pytorch基础知识
1. 张量
Pytorch Tensors是作为所有高级操作的基础的多维阵列变量。与标准数字类型不同,可以分配张量以使用CPU或GPU加速操作。
它们与N维数量数量类似,甚至可以仅在单行中转换为Numpy数组。
张量有5种类型:
- Floattensor:32位 Float
- Doubletensor:64位 Float
- HalfTensor:16位 Float
- Intstensor:32位int
- longtensor:64位int
与所有数字类型一样,您希望使用适合您需要保存内存的最小类型。pytorch使用floattensor作为所有张量的默认类型,但您可以使用此使用
- torch.set_default_tensor_type(t)
初始化两个FloatTensors:
- import torch
- # initializing tensors
- a = torch.tensor(2)
- b = torch.tensor(1)
在简单的数学运算中可以像其他数字类型一样使用张量。
- # addition
- print(a+b)
- # subtraction
- print(b-a)
- # multiplication
- print(a*b)
- # division
- print(a/b)
您还可以使用移动GPU的CUDA处理张量。
- if torch.cuda.is_available():
- xx = x.cuda()
- yy = y.cuda()
- x + y
随着张量在Pytorch中的矩阵,您可以设置Tensors以表示数字表:
- ones_tensor = torch.ones((2, 2)) # tensor containing all ones
- rand_tensor = torch.rand((2, 2)) # tensor containing random values
在这里,我们指定了我们的张量应该是2x2平方。在使用rand()函数时使用vone()函数或随机数时,填充了广场。
2. 神经网络
由于其卓越的分类模型(如图像分类或卷积神经网络(CNN)),Pytorch通常用于构建神经网络。
神经网络是连接和加权数据节点的层。每个图层允许模型在其中分类输入数据最匹配的分类。
神经网络仅与他们的培训一样好,因此需要大数据集和GAN框架,这基于已经由模型掌握的那些产生更具挑战性的培训数据。
Pytorch使用Torch.NN包定义神经网络,其中包含一组模块来表示网络的每层。
每个模块接收输入张量并计算输出张力,该输出张量在一起以创建网络。Torch.nn封装还定义了我们用于训练神经网络的损耗函数。建立神经网络的步骤是:
- 架构:创建神经网络层,设置参数,建立权重和偏见。
- 正向传播:使用参数计算预测的输出。通过比较预测和实际输出来测量误差。
- 反向传播:在找到错误后,在神经网络的参数方面采用错误功能的导数。向后传播允许我们更新我们的权重参数。
- 迭代优化:使用优化器通过使用梯度下降来使用迭代更新参数的优化器来最小化错误。
这是Pytorch中神经网络的示例:
- import torch
- import torch.nn as nn
- import torch.nn.functional as F
- class Net(nn.Module):
- def __init__(self):
- super(Net, self).__init__()
- # 1 input image channel, 6 output channels, 3x3 square convolution
- # kernel
- self.conv1 = nn.Conv2d(1, 6, 3)
- self.conv2 = nn.Conv2d(6, 16, 3)
- # an affine operation: y = Wx + b
- self.fc1 = nn.Linear(16 * 6 * 6, 120) # 6*6 from image dimension
- self.fc2 = nn.Linear(120, 84)
- self.fc3 = nn.Linear(84, 10)
- def forward(self, x):
- # Max pooling over a (2, 2) window
- x = F.max_pool2d(F.relu(self.conv1(x)), (2, 2))
- # If the size is a square you can only specify a single number
- x = F.max_pool2d(F.relu(self.conv2(x)), 2)
- xx = x.view(-1, self.num_flat_features(x))
- x = F.relu(self.fc1(x))
- x = F.relu(self.fc2(x))
- x = self.fc3(x)
- return x
- def num_flat_features(self, x):
- size = x.size()[1:] # all dimensions except the batch dimension
- num_features = 1
- for s in size:
- num_features *= s
- return num_features
- net = Net()
- print(net)
NN.Module指定这将是一个神经网络,然后我们用2个Conv2D层定义它,该层执行2D卷积,以及执行线性变换的3个线性层。
接下来,我们定义了向前概述转发传播的前向方法。我们不需要定义向后传播方法,因为Pytorch默认包括向后()功能。
别担心现在似乎令人困惑,我们将在本教程后面介绍更简单的Pytorch实现。
3. Autograd
Autograd是一个用于计算神经网络操作所必需的衍生产品的Pytorch包。这些衍生物称为梯度。在转发通行证期间,Autograd在梯度的张量上记录所有操作,并创建一个非循环图,以找到张量和所有操作之间的关系。此操作集合称为自动差异化。
该图的叶子是输入张量,根部是输出张量。Autograd通过将图形从根到叶子跟踪并将每个梯度乘以使用链规则来计算渐变来计算梯度。
在计算梯度之后,衍生物的值被自动填充为张量的grad属性。
- import torch
- # pytorch tensor
- x = torch.tensor(3.5, requires_grad=True)
- # y is defined as a function of x
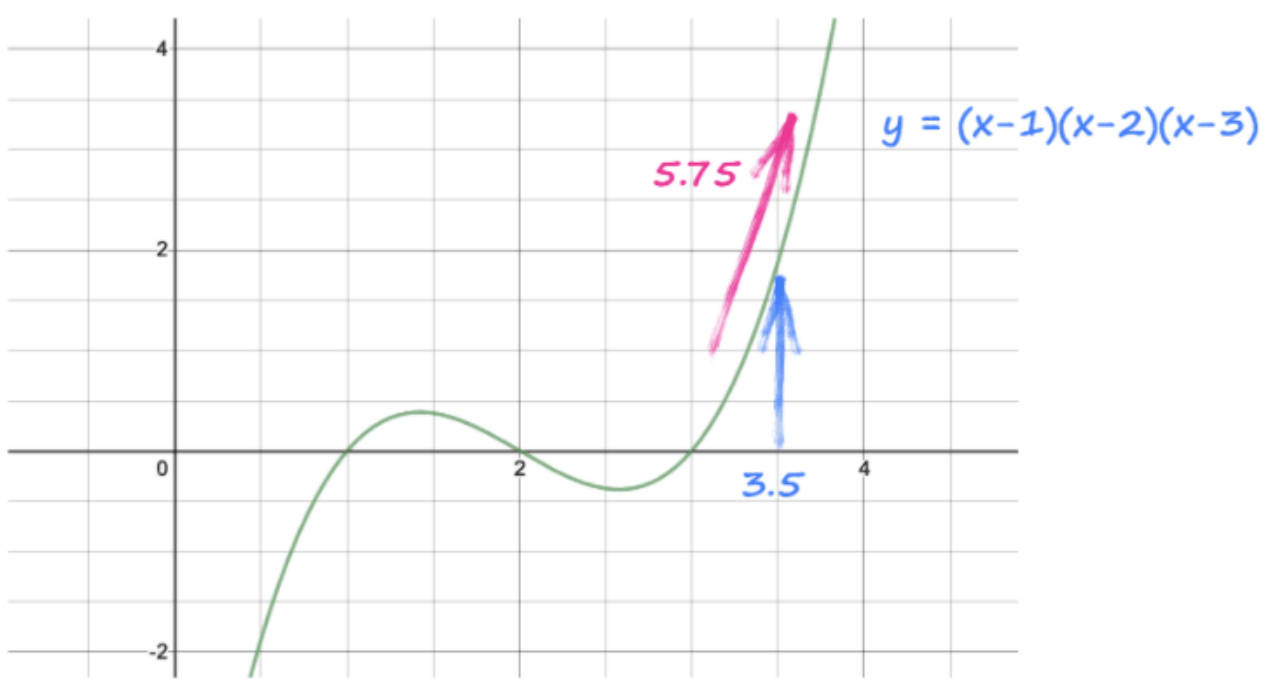
- y = (x-1) * (x-2) * (x-3)
- # work out gradients
- y.backward()
默认情况下,RESCEL_GRAD设置为FALSE,PyTorch不会跟踪渐变。在初始化期间指定RESECT_GRAD为TRUE将使您在执行某些操作的情况下对该特定张量进行PYTORCH跟踪梯度。
此代码查看Y并看到它来自(x-1)(x-2)(x-3),并自动制造梯度dy / dx,3x ^ 2 - 12x + 11
该指令还解决了该梯度的数值,并将其放置在张量x内,同时x,3.5的实际值。
渐变为3 (3.5 3.5) - 12 *(3.5)+ 11 = 5.75。
> Image Source: Author
渐变默认累计,如果未重置,则可能会影响结果。使用Model.zero_grad()在每个渐变后重新归零您的图形。
4. 优化器
优化器允许您在模型中更新权重和偏置以减少错误。这允许您编辑模型的工作原理,而无需重新制止整个事物。
所有Pytorch优化器都包含在Torch.optim包中,每个优化方案都设计用于特定情况。Torch.optim模块允许您通过刚刚传递参数列表来构建抽象优化方案。Pytorch有许多优化器可以选择,这意味着几乎总是一个最适合您的需求。
例如,我们可以实现公共优化算法,SGD(随机梯度下降),以平滑我们的数据。
- import torch.optim as optim
- params = torch.tensor([1.0, 0.0], requires_grad=True)
- learning_rate = 1e-3
- ## SGD
- optimoptimizer = optim.SGD([params], lr=learning_rate)
更新模型后,使用优化器.step()告诉Pytorch来重新计算模型。使用优化器,我们需要使用循环手动更新模型参数:
- for params in model.parameters():
- params -= params.grad * learning_rate
总的来说,优化器通过允许您优化数据加权并改变模型而无需重新制定若需时间来节省大量时间。
5. 使用pytorch计算图
为了更好地了解Pytorch和神经网络,可以使用计算图来练习。这些图形本质上是一种简化版本的神经网络,用于有一系列操作,用于了解系统的输出如何受输入的影响。
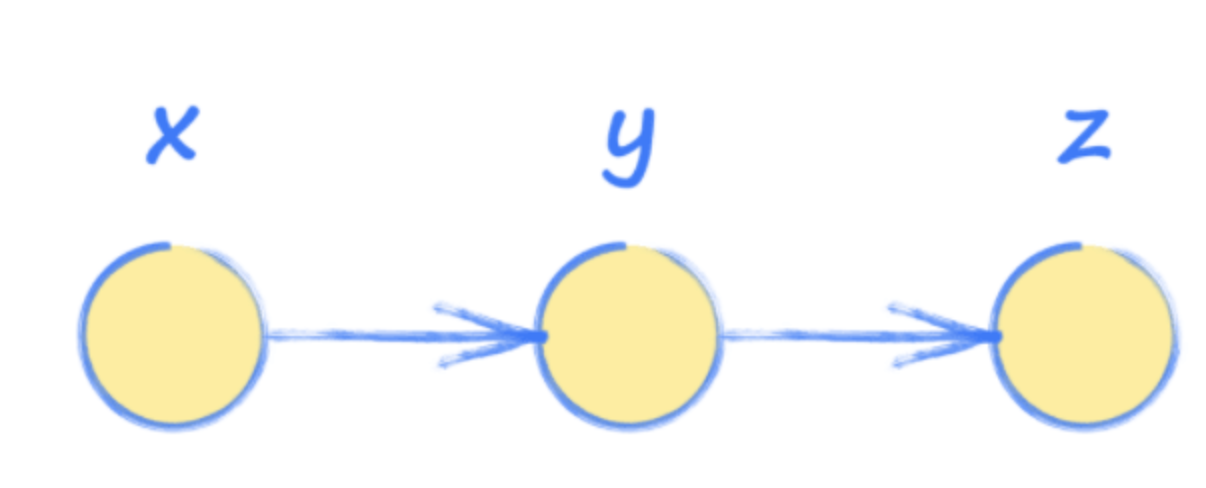
换句话说,输入x用于找到y,然后用于找到输出z。
> Image Source: Author
想象一下,Y和Z计算如下:
- y = x ^ 2
- z = 2Y + 3
但是,我们对输出Z如何使用Input X进行更改感兴趣,因此我们需要执行一些微积分:
- dz / dx =(dz / dy)*(dy / dx)
- dz / dx = 2.2x
- dz / dx = 4x
使用此,我们可以看到输入x = 3.5将使z = 14。
知道如何在其他情况下定义每个张量(根据x,z的y和z,y等方面等)允许pytorch构建这些张量如何连接的图像。
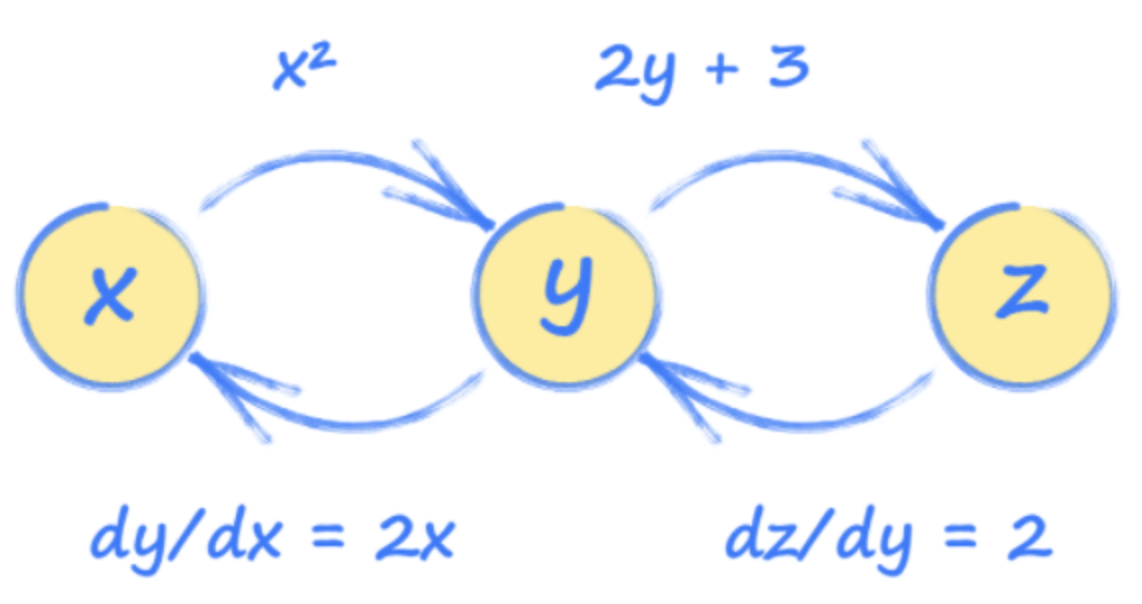
> Image Source: Author
这张照片称为计算图,可以帮助我们了解Pytorch如何在幕后工作。
使用此图形,我们可以看到每个张量如何受到任何其他张量的变化的影响。这些关系是梯度,用于在训练期间更新神经网络。
这些图更容易使用Pytorch比手工操作更容易,所以我们现在试试吧,我们了解幕后发生的事情。
- import torch
- # set up simple graph relating x, y and z
- x = torch.tensor(3.5, requires_grad=True)
- y = x*x
- z = 2*y + 3
- print("x: ", x)
- print("y = x*x: ", y)
- print("z= 2*y + 3: ", z)
- # work out gradients
- z.backward()
- print("Working out gradients dz/dx")
- # what is gradient at x = 3.5
- print("Gradient at x = 3.5: ", x.grad)
这发现Z = 14就像我们用手发现的那样!
6. 与Pytorch的实践:多路径计算图
既然你已经看到了一个具有单一关系的计算图,让我们尝试一个更复杂的例子。
首先,定义两个张量,a和b,以用作我们的输入。确保设置RESECT_GRAD = TRUE,以便我们可以将渐变缩小到下线。
- import torch
- # set up simple graph relating x, y and z
- a = torch.tensor(3.0, requires_grad=True)
- b = torch.tensor(2.0, requires_grad=True)
接下来,设置我们的输入和我们神经网络的每层之间的关系,x,y和z。请注意,z在x和y方面定义,而x和y使用我们的输入值a和b定义。
- import torch
- # set up simple graph relating x, y and z
- a = torch.tensor(3.0, requires_grad=True)
- b = torch.tensor(2.0, requires_grad=True)
- x = 2*a + 3*b
- y = 5*a*a + 3*b*b*b
- z = 2*x + 3*y
这构建了一个关系链,Pytorch可以遵循了解数据之间的所有关系。
我们现在可以通过从z向a追随z到a的路径来解决梯度Dz / da。
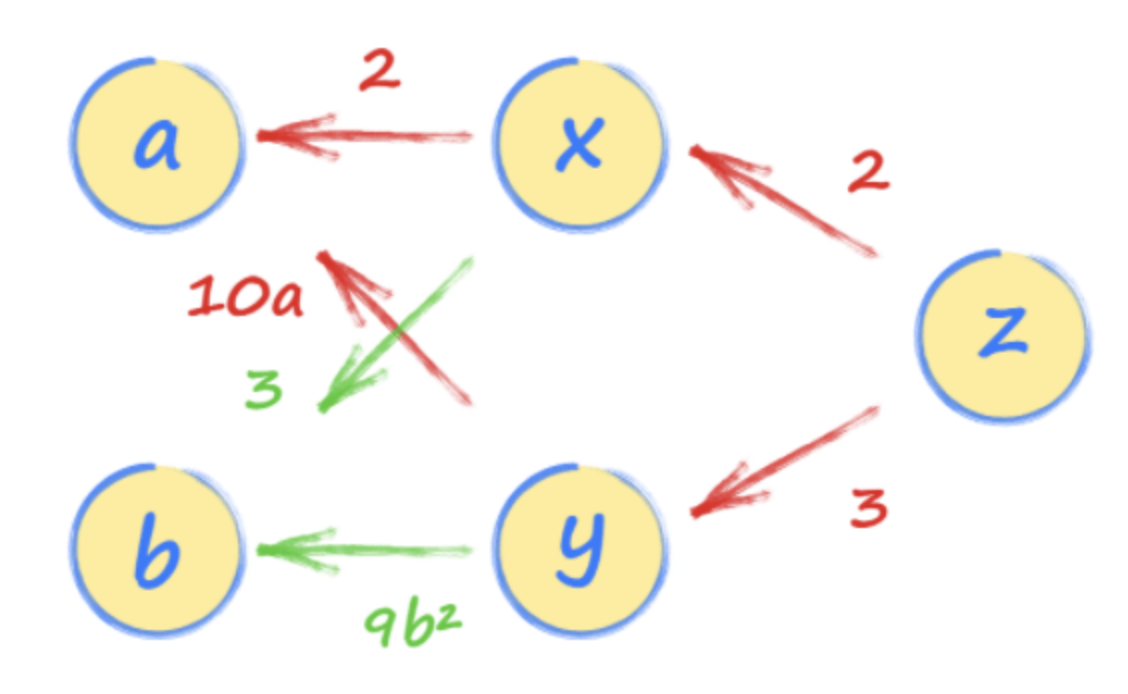
有两条路径,一个通过x和另一条通过y。您应该遵循它们并将两条路径的表达式添加在一起。这是有道理的,因为来自a到z的两条路径有助于z的值。
如果我们使用Chain规则的微积分法定了DZ / DA,我们已经找到了相同的结果。
> Image Source: Author
第一路径X给我们2 * 2,第二条路径通过Y给我们3 * 10A。因此,Z随着4 + 30A而变化的速率。
如果A是22,则DZ / DA为4 + 30 * 2 = 64。
我们可以通过从z添加向后传播然后询问a的梯度(或衍生)来确认它。
- import torch
- # set up simple graph relating x, y and z
- a = torch.tensor(2.0, requires_grad=True)
- b = torch.tensor(1.0, requires_grad=True)
- x = 2*a + 3*b
- y = 5*a*a + 3*b*b*b
- z = 2*x + 3*y
- print("a: ", a)
- print("b: ", b)
- print("x: ", x)
- print("y: ", y)
- print("z: ", z)
- # work out gradients
- z.backward()
- print("Working out gradient dz/da")
- # what is gradient at a = 2.0
- print("Gradient at a=2.0:", a.grad)
你学习的下一步
恭喜,您现在已完成您的快速入门,并且是Pytorch和神经网络。完成计算图形是了解深度学习网络的重要组成部分。
当您了解高级深度学习技能和应用程序时,您将想要探索:
- 复杂的神经网络,优化
- 可视化设计
- 用GAN训练
快乐学习!
原文链接:https://ai.plainenglish.io/pytorch-tutorial-a-quick-guide-for-new-learners-180957cb7214