如何用 JS 实现二叉堆-js二叉树

[[384564]]

前言

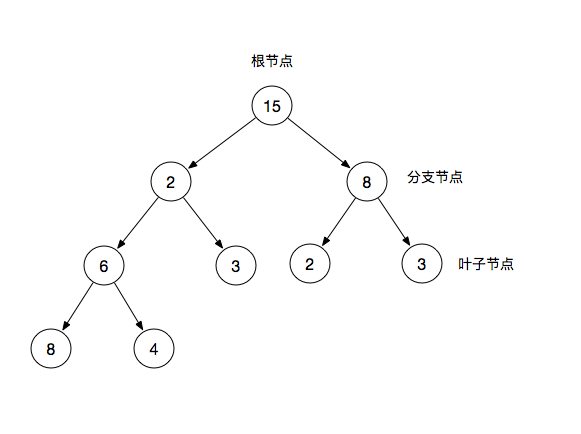
二叉树(Binary Tree)是一种树形结构，它的特点是每个节点最多只有两个分支节点，一棵二叉树通常由根节点、分支节点、叶子节点组成，如下图所示。每个分支节点也常常被称作为一棵子树，而二叉堆是一种特殊的树，它属于完全二叉树。

二叉树与二叉堆的关系

在日常工作中会遇到很多数组的操作，比如排序等。那么理解二叉堆的实现对以后的开发效率会有所提升，下面就简单介绍一下什么是二叉树，什么是二叉堆。

二叉树特征

根节点：二叉树最顶层的节点
分支节点：除了根节点以外且拥有叶子节点
叶子节点：除了自身，没有其他子节点

在二叉树中，我们常常还会用父节点和子节点来描述，比如上图中左侧节点 2 为 6 和 3 的父节点，反之 6 和 3 是 2 子节点。

二叉树分类

二叉树分为满二叉树(full binary tree)和完全二叉树(complete binary tree)。

满二叉树：一棵深度为 k 且有 2 ^ k - 1个节点的二叉树称为满二叉树
完全二叉树：完全二叉树是指最后一层左边是满的，右边可能满也可能不满，然后其余层都是满的二叉树称为完全二叉树(满二叉树也是一种完全二叉树)

二叉树结构

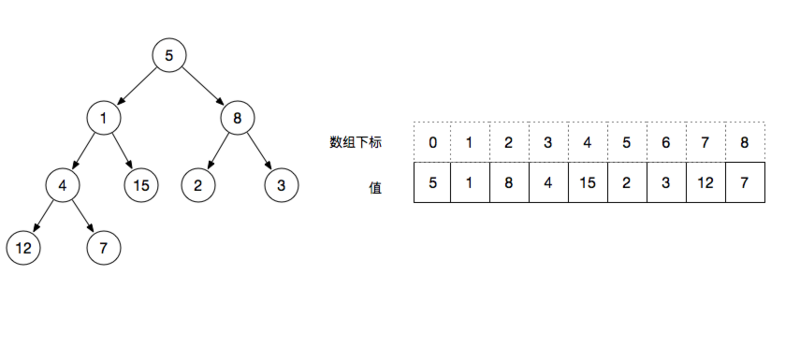
从图中我们可以看出二叉树是从上到下依次排列下来，可想而知可以用一个数组来表示二叉树的结构，从下标 index( 0 - 8 ) 从上到下依次排列。

二叉树左侧节点表达式 index * 2 + 1。例如：以根节点为例求左侧节点，根节点的下标为0，则左侧节点的序数是1 ，对应数组中的值为1
二叉树右侧节点表达式 index * 2 + 2。例如：以根节点为例求右侧节点，根节点的下标为0，则右侧节点的序数是2 ，对应数组中的值为 8
二叉树叶子节点表达式序数 >= floor( N / 2 )都是叶子节点(N是数组的长度)。例如：floor( 9 / 2 ) = 4 ，则从下标 4 开始的值都为叶子节点

二叉堆特征

二叉堆是一个完全二叉树，父节点与子节点要保持固定的序关系，并且每个节点的左子树和右子树都是一个二叉堆。

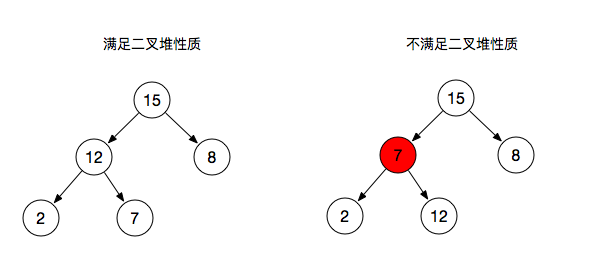
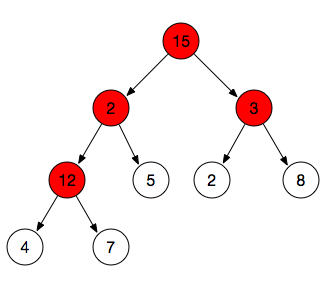
从上图可以看出

图一：每个父节点大于子节点或等于子节点，满足二叉堆的性质
图二：其中有一个父节点小于子节点则不满足二叉堆性质

二叉堆分类

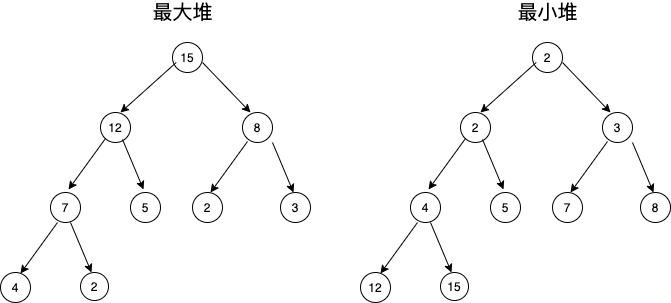
二叉堆根据排序不同，可以分为最大堆和最小堆

最大堆：根节点的键值是所有堆节点键值中最大者，且每个父节点的值都比子节点的值大
最小堆：根节点的键值是所有堆节点键值中最小者，且每个父节点的值都比子节点的值小

如何实现二叉堆

通过上面的讲述想必大家对二叉堆有了一定的理解，那么接下来就是如何实现。以最大堆为例，首先要初始化数组然后通过交换位置形成最大堆。

初始化二叉堆

从上面描述，我们可以知道二叉堆其实就是一个数组，那么初始化就非常简单了。

class Heap{ 
  constructor(arr){ 
    this.data = [...arr]; 
    this.size = this.data.length; 
  } 
}

父子节点交换位置

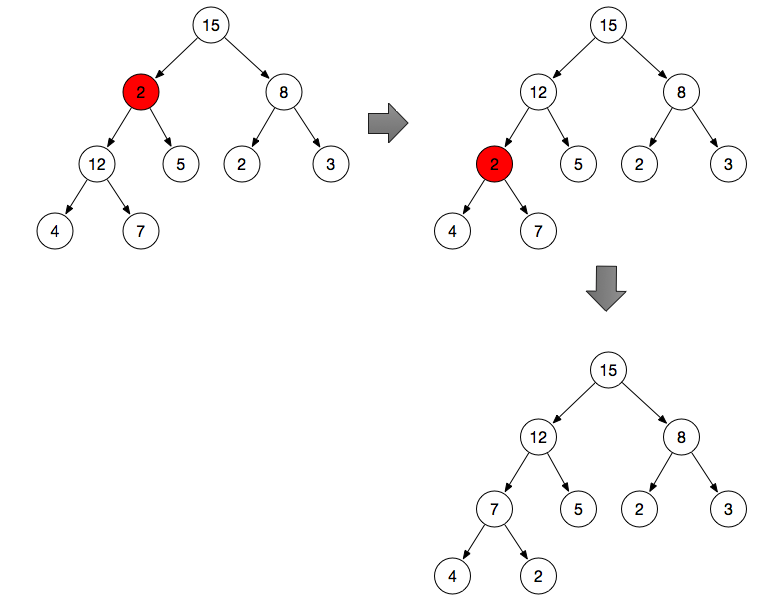
图一中 2 作为父节点小于子节点，很显然不符合最大堆性质。maxHeapify 函数可以把每个不符合最大堆性质的节点调换位置，从而满足最大堆性质的数组。

调整步骤：

调整分支节点 2 的位置(不满足最大堆性质)
获取父节点 2 的左右节点 ( 12 , 5 ) ，从 ( 2 , 15 , 5 ) 中进行比较
找出最大的节点与父节点进行交换，如果该节点本身为最大节点则停止操作
重复 step2 的操作，从 2 , 4 , 7 中找出最大值与 2 做交换(递归)

maxHeapify(i) { 
  let max = i; 
 
  if(i >= this.size){ 
    return; 
  } 
  // 当前序号的左节点 
  const l = i * 2 + 1; 
  // 当前需要的右节点 
  const r = i * 2 + 2; 
 
  // 求当前节点与其左右节点三者中的最大值 
  if(l < this.size && this.data[l] > this.data[max]){ 
    max = l; 
  } 
  if(r < this.size && this.data[r] > this.data[max]){ 
    max = r; 
  } 
 
  // 最终max节点是其本身,则已经满足最大堆性质，停止操作 
  if(max === i) { 
    return; 
  } 
 
  // 父节点与最大值节点做交换 
  const t = this.data[i]; 
  this.data[i] = this.data[max]; 
  this.data[max] = t; 
 
  // 递归向下继续执行 
  return this.maxHeapify(max); 
}

形成最大堆

我们可以看到，初始化是由一个数组组成，以下图为例很显然并不会满足最大堆的性质，上述 maxHeapify 函数只是对某一个节点作出对调，无法对整个数组进行重构，所以我们要依次对数组进行递归重构。

找到所有分支节点 Math.floor( N / 2 )(不包括叶子节点)
将找到的子节点进行 maxHeapify 操作

rebuildHeap(){ 
  // 叶子节点 
  const L = Math.floor(this.size / 2); 
  for(let i = L - 1; i >= 0; i--){ 
    this.maxHeapify(i); 
  } 
}

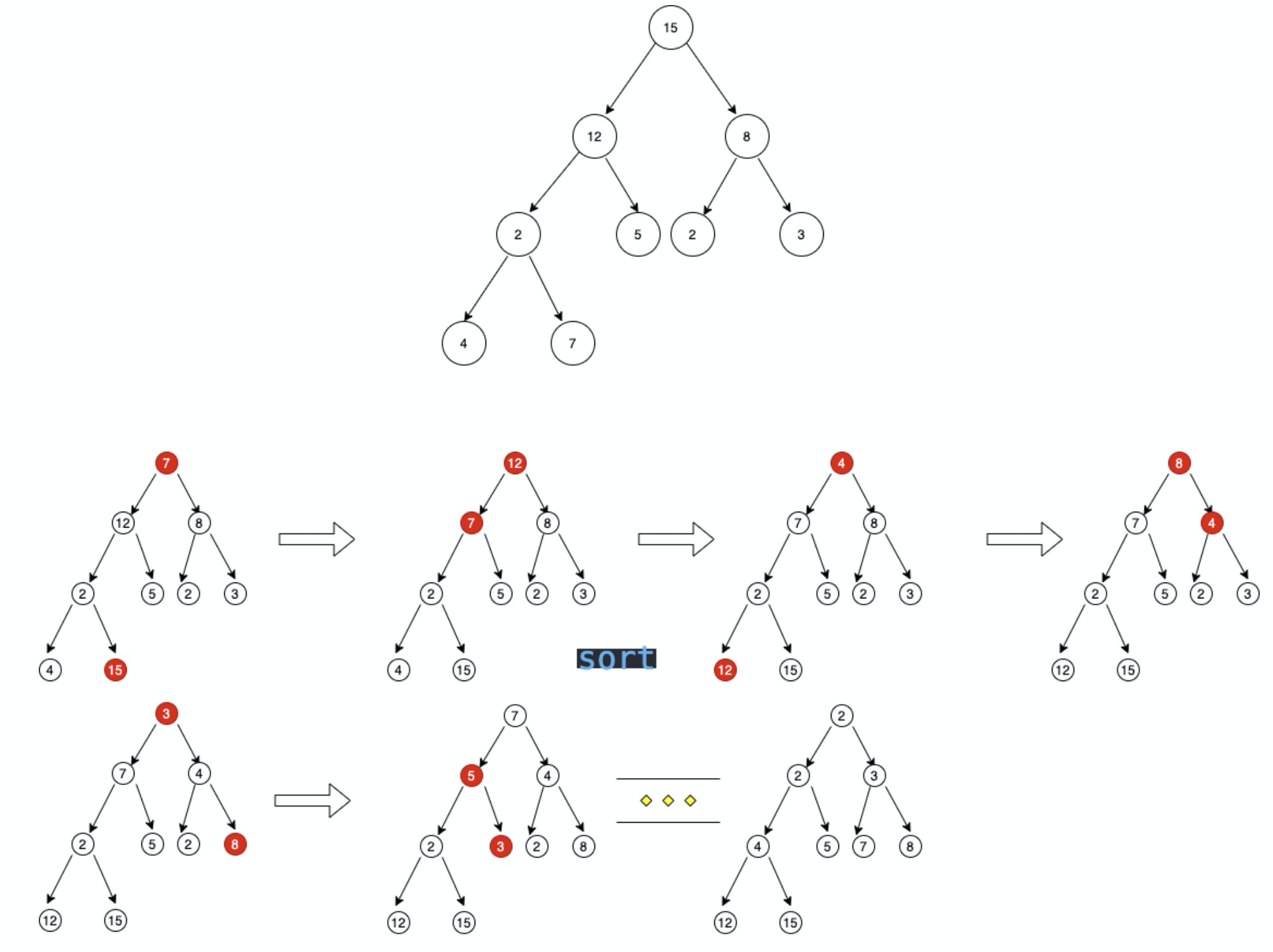
生成一个升序的数组

swap 函数交换首位位置
将最后一个从堆中拿出相当于 size - 1
执行 maxHeapify 函数进行根节点比较找出最大值进行交换
最终 data 会变成一个升序的数组

sort() { 
  for(let i = this.size - 1; i > 0; i--){ 
    swap(this.data, 0, i); 
    this.size--; 
    this.maxHeapify(0); 
  } 
}

插入方法

Insert 函数作为插入节点函数，首先

往 data 结尾插入节点
因为节点追加，size + 1
因为一个父节点拥有 2 个子节点，我们可以根据这个性质通过 isHeap 函数获取第一个叶子节点，可以通过第一个叶子节点获取新插入的节点，然后进行 3 个值的对比，找出最大值，判断插入的节点。如果跟父节点相同则不进行重构(相等满足二叉堆性质)，否则进行 rebuildHeap 重构堆

isHeap() { 
  const L = Math.floor(this.size / 2); 
  for (let i = L - 1; i >= 0; i--) { 
    const l = this.data[left(i)] || Number.MIN_SAFE_INTEGER; 
    const r = this.data[right(i)] || Number.MIN_SAFE_INTEGER; 
 
    const max = Math.max(this.data[i], l, r); 
 
    if (max !== this.data[i]) { 
      return false; 
    } 
    return true; 
  } 
} 
insert(key) { 
  this.data[this.size] = key; 
  this.size++ 
  if (this.isHeap()) { 
    return; 
  } 
  this.rebuildHeap(); 
}

删除方法

delete 函数作为删除节点，首先

删除传入index的节点
因为节点删除，size - 1
重复上面插入节点的操作

delete(index) { 
  if (index >= this.size) { 
    return; 
  } 
  this.data.splice(index, 1); 
  this.size--; 
  if (this.isHeap()) { 
    return; 
  } 
  this.rebuildHeap(); 
}

完整代码

/** 
 * 最大堆 
 */ 
 
function left(i) { 
  return (i * 2) + 1; 
} 
 
function right(i) { 
  return (i * 2) + 2; 
} 
 
function swap(A, i, j) { 
  const t = A[i]; 
  A[i] = A[j]; 
  A[j] = t; 
} 
 
class Heap { 
  constructor(arr) { 
    this.data = [...arr]; 
    this.size = this.data.length; 
    this.rebuildHeap = this.rebuildHeap.bind(this); 
    this.isHeap = this.isHeap.bind(this); 
    this.sort = this.sort.bind(this); 
    this.insert = this.insert.bind(this); 
    this.delete = this.delete.bind(this); 
    this.maxHeapify = this.maxHeapify.bind(this); 
  } 
 
  /** 
   * 重构堆，形成最大堆 
   */ 
  rebuildHeap() { 
    const L = Math.floor(this.size / 2); 
    for (let i = L - 1; i >= 0; i--) { 
      this.maxHeapify(i); 
    } 
  } 
 
  isHeap() { 
    const L = Math.floor(this.size / 2); 
    for (let i = L - 1; i >= 0; i--) { 
      const l = this.data[left(i)] || Number.MIN_SAFE_INTEGER; 
      const r = this.data[right(i)] || Number.MIN_SAFE_INTEGER; 
 
      const max = Math.max(this.data[i], l, r); 
 
      if (max !== this.data[i]) { 
        return false; 
      } 
      return true; 
    } 
  } 
 
  sort() { 
    for (let i = this.size - 1; i > 0; i--) { 
      swap(this.data, 0, i); 
      this.size--; 
      this.maxHeapify(0); 
    } 
  } 
 
  insert(key) { 
    this.data[this.size++] = key; 
    if (this.isHeap()) { 
      return; 
    } 
    this.rebuildHeap(); 
  } 
 
  delete(index) { 
    if (index >= this.size) { 
      return; 
    } 
    this.data.splice(index, 1); 
    this.size--; 
    if (this.isHeap()) { 
      return; 
    } 
    this.rebuildHeap(); 
  } 
 
  /** 
   * 交换父子节点位置，符合最大堆特征 
   * @param {*} i 
   */ 
  maxHeapify(i) { 
    let max = i; 
 
    if (i >= this.size) { 
      return; 
    } 
 
    // 求左右节点中较大的序号 
    const l = left(i); 
    const r = right(i); 
    if (l < this.size && this.data[l] > this.data[max]) { 
      max = l; 
    } 
 
    if (r < this.size && this.data[r] > this.data[max]) { 
      max = r; 
    } 
 
    // 如果当前节点最大，已经是最大堆 
    if (max === i) { 
      return; 
    } 
 
    swap(this.data, i, max); 
 
    // 递归向下继续执行 
    return this.maxHeapify(max); 
  } 
} 
 
module.exports = Heap;

示例

相信通过上面的讲述大家对最大堆的实现已经有了一定的理解，我们可以利用这个来进行排序。

const arr = [15, 12, 8, 2, 5, 2, 3, 4, 7]; 
const fun = new Heap(arr); 
fun.rebuildHeap(); // 形成最大堆的结构 
fun.sort();// 通过排序，生成一个升序的数组 
console.log(fun.data) // [2, 2, 3, 4, 5, 7, 8, 12, 15]

总结

文章中主要讲述了二叉树、二叉堆的概念，然后通过代码实现二叉堆。我们可以通过二叉堆来做排序和优先级队列等。