在任何数据科学应用中,观察偏差和亚组差异很容易产生统计悖论。因此,忽略这些因素会完全破坏我们的分析结论。
观察到令人惊讶的现象,例如在汇总数据中完全还原的子组趋势,的确不罕见。在本文中,我们研究了数据科学中遇到的三种最常见的统计悖论。
1. 伯克森悖论
第一个引人注目的例子是观察到的COVID-19严重程度与吸烟之间的负相关性(例如,参见Wenzel 2020年的欧盟委员会审查)。吸烟是呼吸系统疾病的众所周知的危险因素,那么我们如何解释这种矛盾呢?
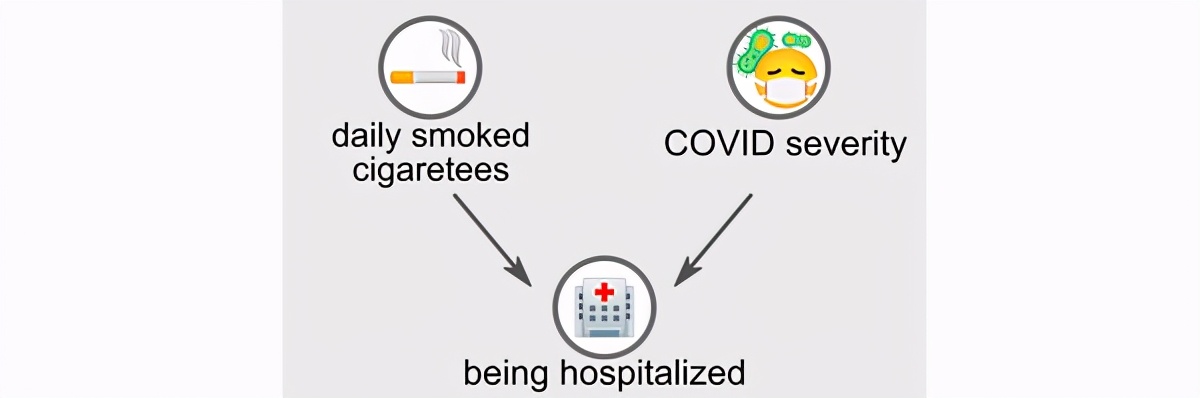
最近在《自然》杂志上发表的2020年格里菲斯(Griffith 2020)的工作表明,这可能是Collider Bias(也称为Berkson悖论)的例子。为了理解这一悖论,让我们考虑以下图形模型,其中包括第三个随机变量:“正在住院”。
第三个变量“正在住院”是前两个变量的对撞者。这意味着吸烟和严重COVID-19都会增加在医院生病的机会。当我们以对撞机为条件时,即当我们仅观察住院患者的数据而不考虑整个人口时,伯克森悖论恰好出现。
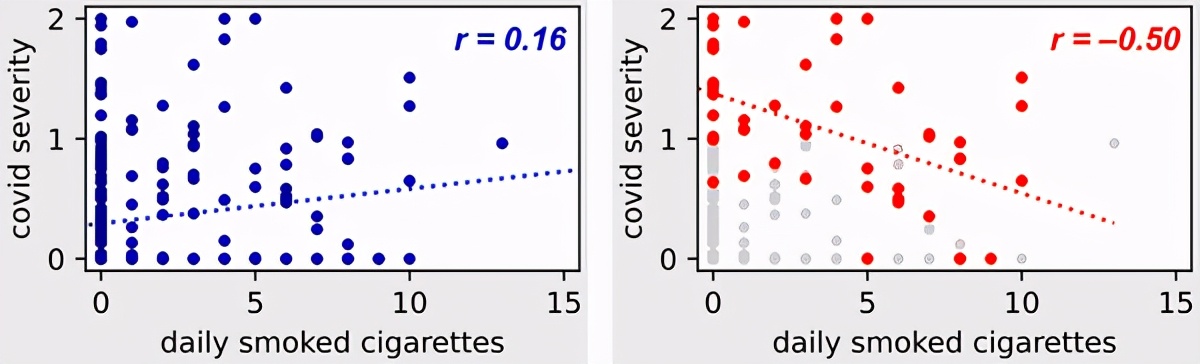
让我们考虑以下示例数据集。在左图中,我们观察到了整个人群,而在右图中,我们仅考虑了一部分住院患者(即,我们以对撞机变量为条件)。
在左图中,我们可以观察到COVID-19严重程度与吸烟之间的正相关关系,因为我们知道吸烟是呼吸系统疾病的危险因素,因此我们可以预期。
但是在正确的数字上(我们只考虑住院患者),我们看到了相反的趋势!要理解这一点,请考虑以下几点。
- 严重程度较高的COVID-19会增加住院的机会。特别是,如果严重程度大于1,则需要住院治疗。
- 每天抽几支烟是多种疾病(心脏病,癌症,糖尿病)的主要危险因素,由于某种原因,这些疾病增加了住院的机会。
- 因此,如果住院患者的COVID-19严重程度较低,则他们吸烟的机会更高!实际上,他们必须患有与COVID-19不同的某种疾病(例如心脏病,癌症,糖尿病)以证明其住院治疗的合理性,而这种疾病很可能是由吸烟引起的。
这个例子与伯克森1946年的原始工作非常相似,作者发现医院患者的胆囊炎和糖尿病之间存在负相关关系,尽管糖尿病是胆囊炎的危险因素。
2. 潜在变量
潜在变量的存在还可能在两个变量之间产生明显相反的相关性。尽管伯克森的悖论是由于对撞机变量的条件而出现的(因此应避免使用),但可以通过对潜变量的条件来解决另一种悖论。
例如,让我们考虑一下扑灭火灾的消防员人数与火灾中受伤人数之间的关系。我们希望拥有更多的消防员会改善结果(在某种程度上,请参见布鲁克斯定律),但是在汇总数据中却发现存在正相关关系:部署的消防员越多,受伤人数越多!
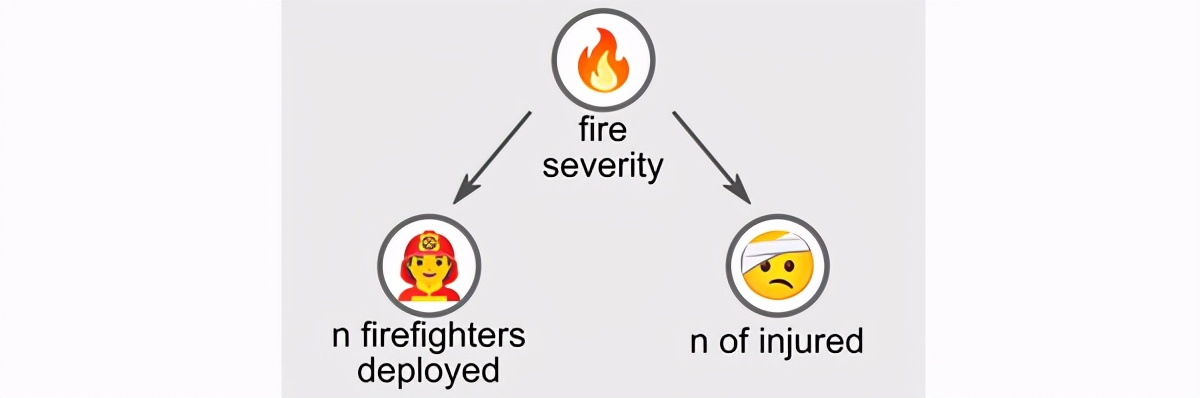
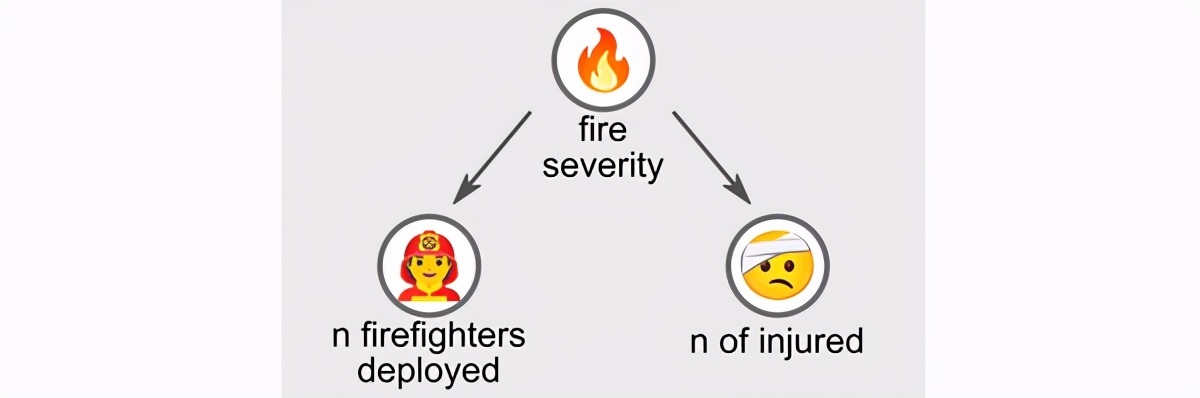
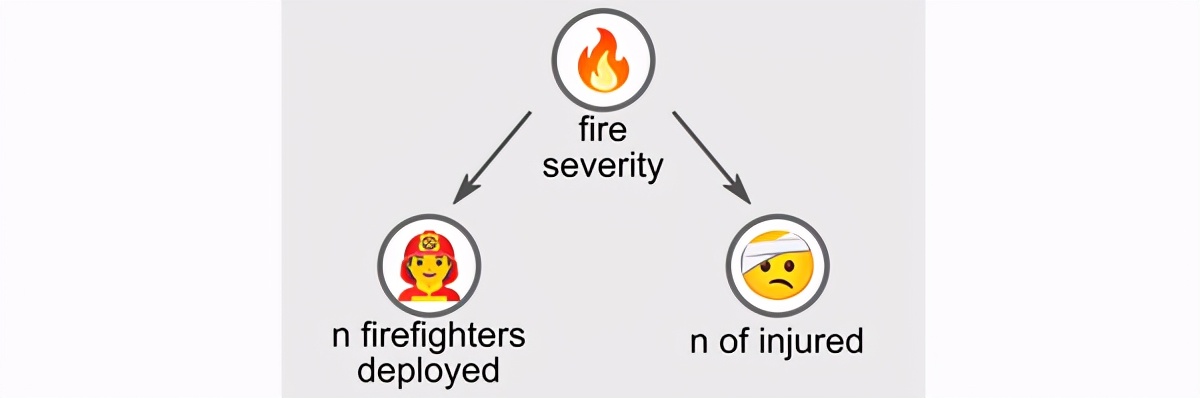
为了理解这种矛盾,让我们考虑以下图形模型。关键是再次考虑第三个随机变量:“火灾严重性”。
该第三潜在变量与其他两个正相关。确实,更严重的火灾往往会造成更多的伤害,同时又需要更多的消防员被扑灭。
让我们考虑以下示例数据集。在左图中,我们汇总了来自各种火灾的观测值,而在右图中,我们仅考虑了与三个固定程度的火灾严重性相对应的观测值(即,我们将观测值设置为潜变量)。
在右图中,我们根据火势的严重程度对观测值进行了条件调整,可以看到我们期望的负相关。
- 对于给定的严重程度的火灾,我们确实可以观察到,消防员部署的越多,受伤的人就越少。
- 如果我们着眼于严重程度较高的火灾,即使部署的消防员人数和受伤人数都较高,我们也会观察到相同的趋势。
3. 辛普森悖论
当在子组中始终观察到趋势时出现辛普森悖论,这是一个令人惊讶的现象,但是如果合并子组,则趋势会反转。它通常与数据子组中的类不平衡有关。
这个悖论的一个臭名昭著的发生是在比克尔(Bickel)1975年进行的,当时对加利福尼亚大学的录取率进行了分析,以发现性别歧视的证据,并揭示了两个明显矛盾的事实。
- 一方面,他观察到每个部门的女性申请人的录取率均高于男性申请人。
- 另一方面,总数表明,女性申请人的录取率低于男性申请人。
为了了解如何做到这一点,让我们考虑以下两个A部门和B部门的数据集。
- 在100名男性申请人中:接受了A部门申请的80名和68名(85%),而接受B部门申请的20名和12名(60%)被接受。
- 在100名女性申请人中:接受了A部门申请的30名和28名(93%),而接受B部门申请的70名和46名(66%)被接受。
悖论由以下不等式表示。
现在,我们可以了解我们看似矛盾的观察的起源了。关键是在两个部门中,每个部门的申请者的性别存在严重的失衡(部门A:80–30,部门B:20–70)。确实,大多数女学生申请了竞争更激烈的B部门(录取率较低),而大多数男学生则申请了竞争较弱的A部门(录取率较高)。这导致了我们的矛盾观察。
结论
潜在变量,对撞机变量和类不平衡会在许多数据科学应用程序中轻易产生统计悖论。因此,必须特别注意这些关键点,以正确得出趋势并分析结果。
原文链接:https://towardsdatascience.com/top-3-statistical-paradoxes-in-data-science-e2dc37535d99