今天来给大家普及一下霍夫曼编码(Huffman Coding),一种用于无损数据压缩的熵编码算法,由美国计算机科学家大卫·霍夫曼在 1952 年提出——这么专业的解释,不用问,来自维基百科了。
说实话,很早之前我就听说过霍夫曼编码,除了知道它通常用于 GZIP、BZIP2、PKZIP 这些常规的压缩格式中,我还知道它通常用于压缩重复率比较高的字符数据。
大家想啊,英文就 26 个字母进行的无限组合,重复率高得一逼啊!常用的汉字也不多,2500 个左右,别问我怎么知道的,我有问过搜索引擎的。
字符重复的频率越高,霍夫曼编码的工作效率就越高!
是时候,和大家一起来了解一下霍夫曼编码的工作原理啦,毕竟一名优秀的程序员要能做到知其然知其所以然——请允许我又用了一次这句快用臭了话。
假设下面的字符串要通过网络发送。
大家应该知道,每个字符占 8 个比特,上面这串字符总共有 15 个字符,所以一共要占用 15*8=120 个比特。没有疑问吧?有疑问的同学请不好意思下。
如果我们使用霍夫曼编码的话,就可以将这串字符压缩到一个更小的尺寸。怎么做到的呢?
霍夫曼编码首先会使用字符的频率创建一棵树,然后通过这个树的结构为每个字符生成一个特定的编码,出现频率高的字符使用较短的编码,出现频率低的则使用较长的编码,这样就会使编码之后的字符串平均长度降低,从而达到数据无损压缩的目的。
拿上面这串初始字符来一步步的说明下霍夫曼编码的工作步骤。
第一步,计算字符串中每个字符的频率。
B 出现 1 次,C 出现 6 次,A 出现 5 次,D 出现 3 次。
第二步,按照字符出现的频率进行排序,组成一个队列 Q。
出现频率最低的在前面,出现频率高的在后面。
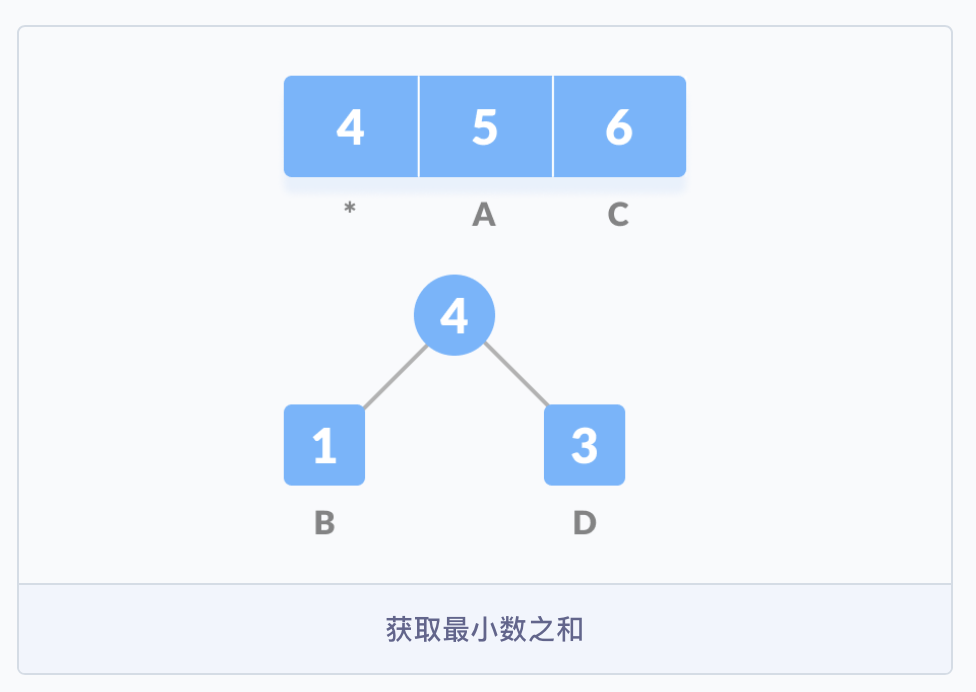
第三步,把这些字符作为叶子节点开始构建一颗树。首先创建一个空节点 z,将最小频率的字符分配给 z 的左侧,并将频率排在第二位的分配给 z 的右侧,然后将 z 赋值为两个字符频率的和。
B 的频率最小,所以在左侧,然后是频率为 3 的 D,在右侧;然后把它们的父节点的值设为 4,子节点的频率之和。
然后从队列 Q 中删除 B 和 D,并将它们的和添加到队列中,上图中 * 表示的位置。紧接着,重新创建一个空的节点 z,并将 4 作为左侧的节点,频率为 5 的 A 作为右侧的节点,4 与 5 的和作为父节点。
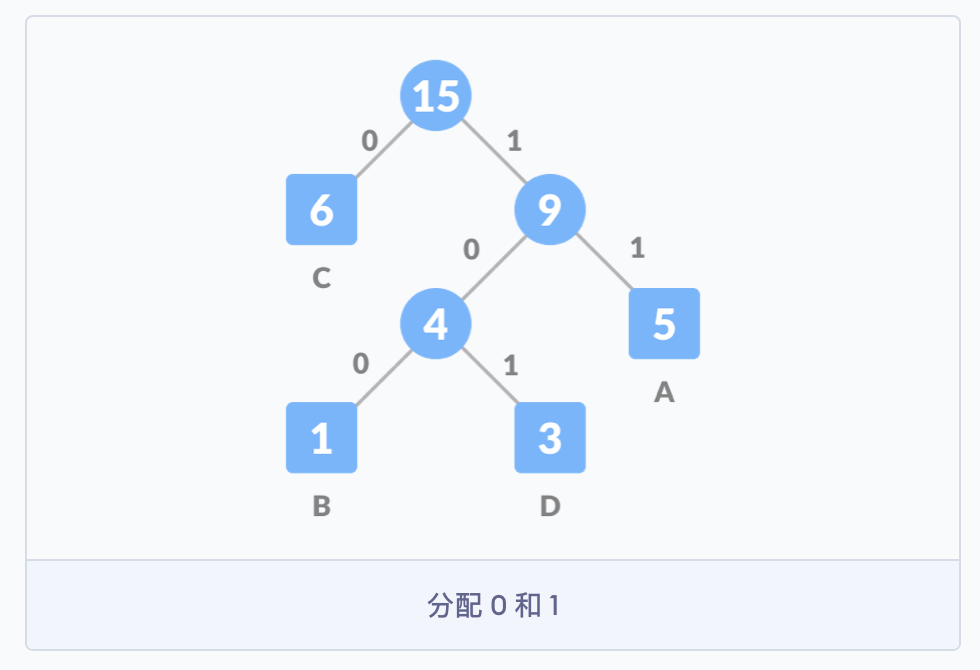
继续按照之前的思路构建树,直到所有的字符都出现在树的节点中。
第四步,对于每个非叶子节点,将 0 分配给连接线的左侧,1 分配给连接线的右侧。此时,霍夫曼树就构建完成了。霍夫曼树又称为最优二叉树,是一种带权路径长度最短的二叉树。
当树构建完毕后,我们来统计一下要发送的比特数。
1)来看字符这一列。四个字符 A、B、C、D 共计 4*8=32 比特。每个英文字母均占用一个字节,即 8 个比特。
2)来看频率这一列。A 5 次,B 1 次,C 6 次,D 3 次,一共 15 比特。
3)来看编码这一列。A 的编码为 11,对应霍夫曼树上的 15→9→5,也就是说,从根节点走到叶子节点 A,需要经过 11 这条路径;对应的 B 需要走过 100 这条路径;对应的 D 需要走过 101 这条路径;对应的 C 需要走过 0 这条路径。
4)来看长度这一列。A 的编码为 11,出现了 5 次,因此占用 10 个比特,即 1111111111;B 的编码为 100,出现了 1 次,因此占用 3 个比特,即 100;C 的编码为 0,出现了 6 次,因此占用 6 个比特,即 000000;D 的编码为 101,出现了 3 次,因此占用 9 个比特,即 101101101。
哈夫曼编码从本质上讲,是将最宝贵的资源(最短的编码)给出现概率最多的数据。在上面的例子中,C 出现的频率最高,它的编码为 0,就省下了不少空间。
结合生活中的一些情况想一下,也是这样,我们把最常用的放在手边,这样就能提高效率,节约时间。所以,我有一个大胆的猜想,霍夫曼就是这样发现编码的最优解的。
在没有经过霍夫曼编码之前,字符串“BCAADDDCCACACAC”的二进制为:
- 10000100100001101000001010000010100010001000100010001000100001101000011010000010100001101000001010000110100000101000011
也就是占了 120 比特。
编码之后为:
- 0000001001011011011111111111
占了 28 比特。
但考虑到解码,需要把霍夫曼树的结构也传递过去,于是字符占用的 32 比特和频率占用的 15 比特也需要传递过去。总体上,编码后比特数为 32 + 15 + 28 = 75,比 120 比特少了 45 个,效率还是非常高的。
关于霍夫曼编码的 Java 示例,我在这里也贴出来一下,供大家参考。
- class HuffmanNode {
- int item;
- char c;
- HuffmanNode left;
- HuffmanNode right;
- }
- class ImplementComparator implements Comparator<HuffmanNode> {
- public int compare(HuffmanNode x, HuffmanNode y) {
- return x.item - y.item;
- }
- }
- public class Huffman {
- public static void printCode(HuffmanNode root, String s) {
- if (root.left == null && root.right == null && Character.isLetter(root.c)) {
- System.out.println(root.c + " | " + s);
- return;
- }
- printCode(root.left, s + "0");
- printCode(root.right, s + "1");
- }
- public static void main(String[] args) {
- int n = 4;
- char[] charArray = { 'A', 'B', 'C', 'D' };
- int[] charfreq = { 5, 1, 6, 3 };
- PriorityQueue<HuffmanNode> q = new PriorityQueue<HuffmanNode>(n, new ImplementComparator());
- for (int i = 0; i < n; i++) {
- HuffmanNode hn = new HuffmanNode();
- hn.c = charArray[i];
- hn.item = charfreq[i];
- hn.left = null;
- hn.right = null;
- q.add(hn);
- }
- HuffmanNode root = null;
- while (q.size() > 1) {
- HuffmanNode x = q.peek();
- q.poll();
- HuffmanNode y = q.peek();
- q.poll();
- HuffmanNode f = new HuffmanNode();
- f.item = x.item + y.item;
- f.c = '-';
- f.left = x;
- f.right = y;
- root = f;
- q.add(f);
- }
- System.out.println(" 字符 | 霍夫曼编码 ");
- System.out.println("--------------------");
- printCode(root, "");
- }
- }
本例的输出结果如下所示:
- 字符 | 霍夫曼编码
- --------------------
- C | 0
- B | 100
- D | 101
- A | 11
给大家留个作业题吧,考虑一下霍夫曼编码的时间复杂度,知道的同学可以在留言区给出答案哈。
搞定,我敢肯定辣条不用吃了——因为大家肯定都学会了。我是爱学习爱美貌的沉默王二,我们下期见,see you~
本文转载自微信公众号「沉默王二」,可以通过以下二维码关注。转载本文请联系沉默王二公众号。