假设您的任务是训练ML模型，以将数据点分类为一定数量的预定义类。 一旦完成分类模型的构建，下一个任务就是评估其性能。 有许多指标可以帮助您根据用例进行操作。 在此文章中，我们将尝试回答诸如何时使用? 它是什么? 以及如何实施?
混淆矩阵
混淆矩阵定义为(类x类)大小的矩阵，因此对于二进制分类，它是2x2，对于3类问题，它是3x3，依此类推。 为简单起见，让我们考虑二元分类并了解矩阵的组成部分。
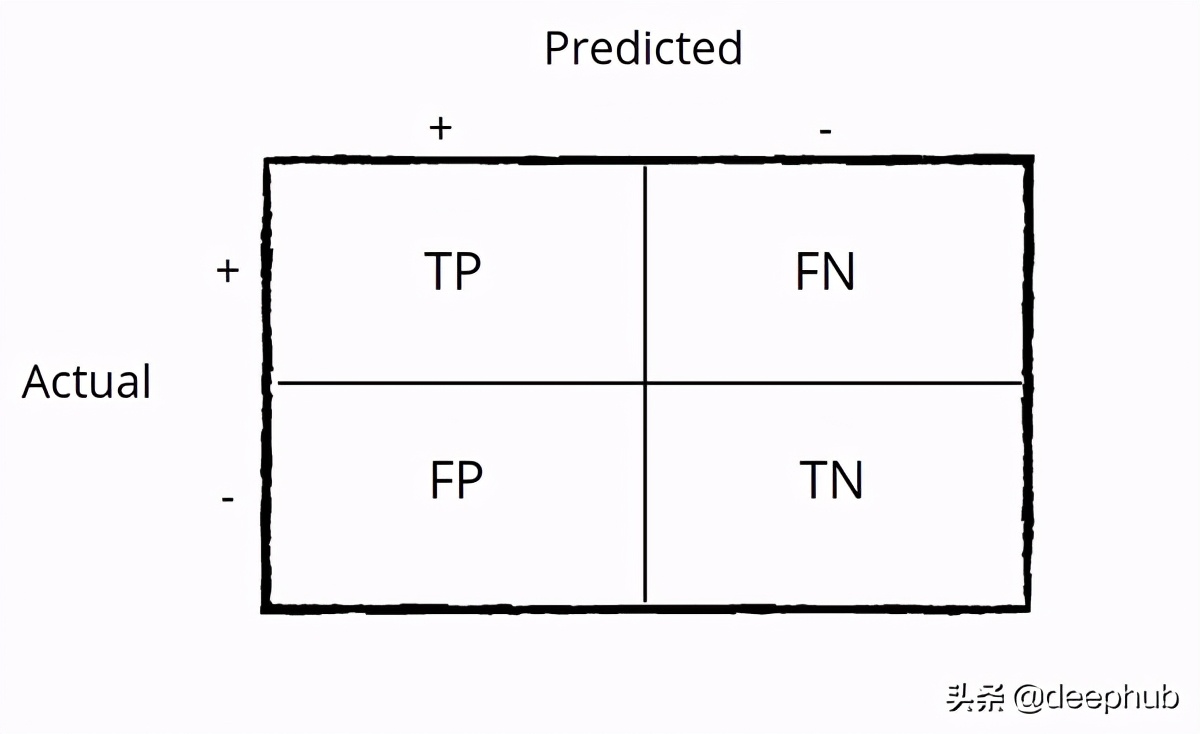
真实正值(TP)-表示该类为“真值”的次数，您的模型也表示它为“真值”。 真负数(TN)-表示该类为假值的次数，您的模型也表示它为假值。 误报(FP)-表示该类为假值，但您的模型表示为真值。
您可以通过这种方式记住它—您的模型错误地认为它是肯定的
假阴性(FN)-表示该类为“真值”的次数，但您的模型表示为“假值”。
您可以通过这种方式记住它-您的模型错误地认为它是假值的
您可以使用sklearn轻松获得混淆矩阵，如下所示-
- from sklearn import metricsdef calculate_confusion_matrix(y, y_pred):
- return metrics.confusion_matrix(y, y_pred)
如图1所示，混淆矩阵的成分是TP，TN，FP，FN，您也可以使用普通python计算它们，如下所示- 计算TP，TN，FP，FN
- def calculate_TP(y, y_pred):
- tp = 0
- for i, j in zip(y, y_pred):
- if i == j == 1:
- tp += 1
- return tp
- def calculate_TN(y, y_pred):
- tn = 0
- for i, j in zip(y, y_pred):
- if i == j == 0:
- tn += 1
- return tn
- def calculate_FP(y, y_pred):
- fp = 0
- for i, j in zip(y, y_pred):
- if i == 0 and j == 1:
- fp += 1
- return fp
- def calculate_FN(y, y_pred):
- fn = 0
- for i, j in zip(y, y_pred):
- if i == 1 and j == 0:
- fn += 1
- return fn
混淆矩阵对于理解模型的细粒度性能很重要，然后根据用例的敏感性，可以确定此模型是否良好。 例如，在医学诊断用例中，您希望模型的假阴性率非常低，因为您不希望系统在测试该人的任何疾病的踪迹时如果事实为“是”，则说“否”。 您仍然可以设法使误报率偏高，因为此人可以通过相关测试并在以后的阶段得到确认。
准确率 Accuracy
准确使人们对模型的运行方式有了整体认识。 但是，如果使用不正确，它很容易高估这些数字。 例如-如果类标签的分布偏斜，则仅预测多数类会给您带来高分(高估性能)，而对于平衡类而言，准确性更有意义。
您可以使用sklearn轻松获得准确性得分，如下所示-
- from sklearn import metrics
- def calculate_accuracy_sklearn(y, y_pred):
- return metrics.accuracy_score(y, y_pred)
也可以使用Python从混淆矩阵组件中计算出来，如下所示-
- def calculate_accuracy(y, y_pred):
- tp = calculate_TP(y, y_pred)
- tn = calculate_TN(y, y_pred)
- fp = calculate_FP(y, y_pred)
- fn = calculate_FN(y, y_pred)
- return (tp+tn) / (tp+tn+fp+fn)
精度 Precision
精度度量有助于我们理解识别阳性样本的正确性%。例如，我们的模型假设有80次是正的，我们精确地计算这80次中有多少次模型是正确的。
也可以计算如下-
- def calculate_precision(y, y_pred):
- tp = calculate_TP(y, y_pred)
- fp = calculate_FP(y, y_pred)
- return tp / (tp + fp)
召回率 Recall
召回指标可帮助我们了解模型能够正确识别的所有地面真实正样本中正样本的百分比。 例如-假设数据中有100个阳性样本，我们计算出该100个样本中有多少个模型能够正确捕获。
也可以如下所示进行计算-
- def calculate_recall(y, y_pred):
- tp = calculate_TP(y, y_pred)
- fn = calculate_FN(y, y_pred)
- return tp / (tp + fn)
对于那些将概率作为输出的模型，调整阈值然后填充相关的混淆矩阵和其他属性始终是一个好习惯。 可以绘制不同阈值的精确召回曲线，并根据用例的敏感性选择阈值。
- def precision_recall_curve(y, y_pred):
- y_pred_class,precision,recall = [],[],[]
- thresholds = [0.1, 0.2, 0.3, 0.6, 0.65]
- for thresh in thresholds:
- for i in y_pred: #y_pred holds prob value for class 1
- if i>=thresh: y_pred_class.append(1)
- else: y_pred_class.append(0)
- precision.append(calculate_precision(y, y_pred_class))
- recall.append(calculate_recall(y, y_pred_class))
- return recall, precisionplt.plot(recall, precision)
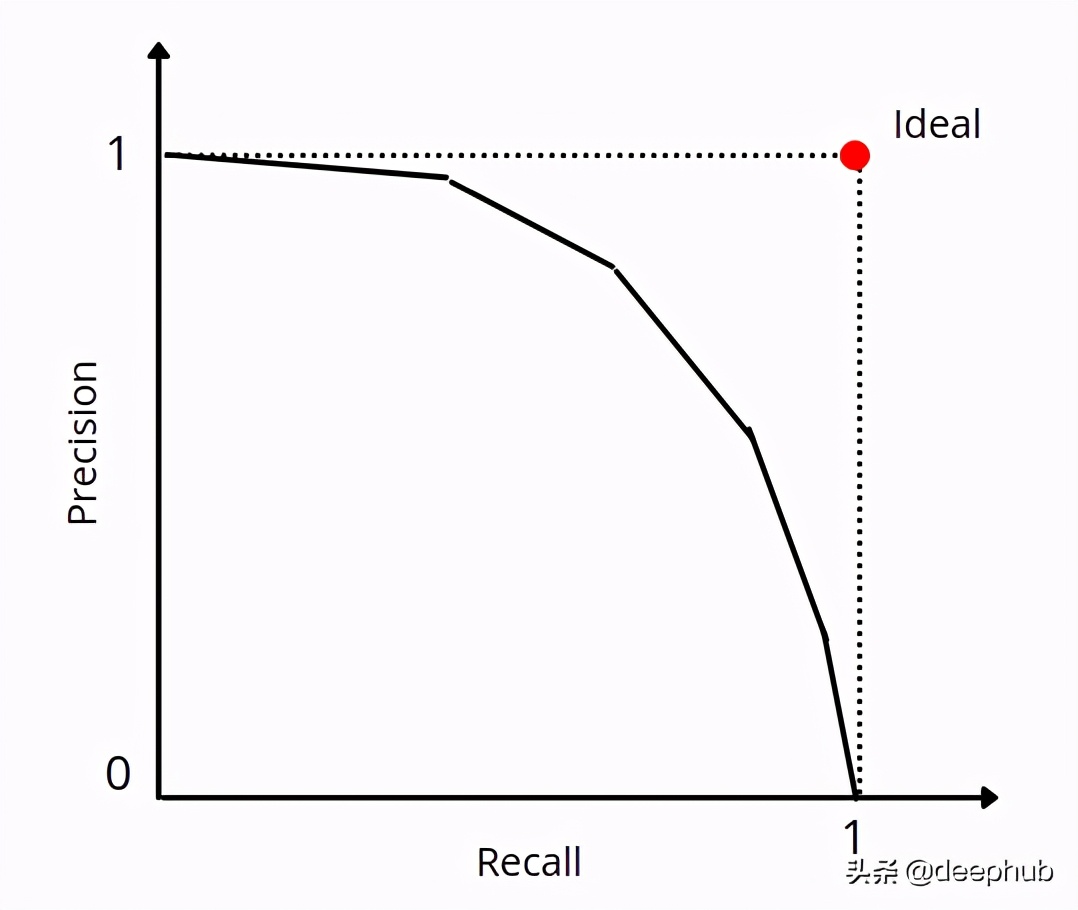
F1分数
F1结合了Precision和Recall得分，得到一个单一的数字，可以帮助直接比较不同的模型。 可以将其视为P和R的谐波均值。谐波均值是因为与其他方式不同，它对非常大的值不敏感。 当处理目标倾斜的数据集时，我们通常考虑使用F1而不是准确性。
您可以如下所示进行计算-
- def calculate_F1(y, y_pred):
- p = calculate_precision(y, y_pred)
- r = calculate_recall(y, y_pred)
- return 2*p*r / (p+r)
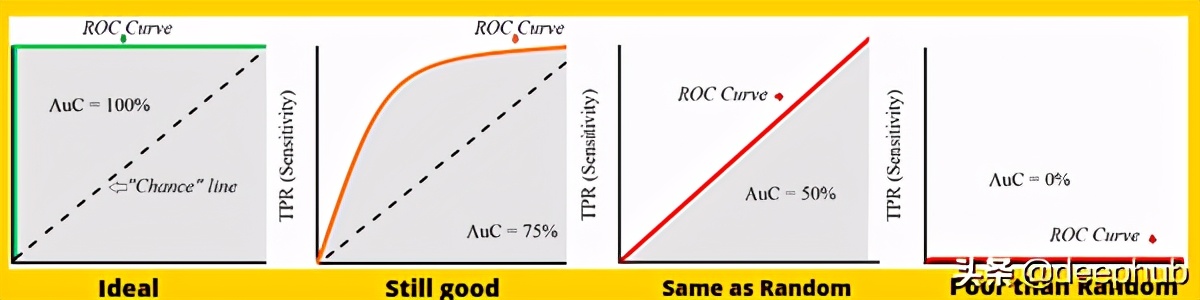
AUC-ROC
AUC-ROC是用于二分类问题的非常常见的评估指标之一。 这是一条曲线，绘制在y轴的TPR(正确率)和x轴的FPR(错误率)之间，其中TPR和FPR定义为-
如果您注意到，TPR和Recall具有相同的表示形式，就像您正确分类了多少正确样本一样。 另一方面，FPR是被错误分类的负面示例的比例。 ROC图总结了每个阈值的分类器性能。 因此，对于每个阈值，我们都有TPR和FPR的新混淆矩阵值，这些值最终成为ROC 2-D空间中的点。 ROC曲线下的AUC(曲线下的面积)值越接近1，模型越好。 这意味着一般而言，对于具有较高AUC的每个阈值，我们的模型都比其他模型具有更好的性能。
您可以如下所示进行计算-
- from sklearn.metrics import roc_auc_score
- def roc_auc(y, y_pred):
- return roc_auc_score(y, y_pred)
Precision @ k
Precision @ k是用于多标签分类设置的流行指标之一。 在此之下，我们计算给定示例的前k个预测，然后计算出这k个预测中有多少个实际上是真实标签。 我们将Precision @ k计算为-
Precision@k = (# of correct predictions from k) / (# of items in k)
- actual_label = [1, 1, 0, 0, 1]
- predicted_label = [1, 1, 1, 0, 0]
- Let k=3
- Precision@k = 2/3 (It's same as TP/(TP+FP))
log损失
当您遇到二分类问题时，log损失是相当不错的。 当您有一个模型输出概率时，该模型将使用该模型，该模型会根据预测与实际标签的偏差来考虑预测的不确定性。
您可以如下所示进行计算-
- def calculate_log_loss(y, y_pred_probs):
- log_loss = -1.0*(t*log(p) + (1-t)*(t*log(1-p))
- return log_loss
在不平衡数据集的情况下，您还可以添加类权重来惩罚少数类相对于多数类的错误。在代码中，w1和w2分别对应正类和负类的权重。
- def calculate_log_loss_weighted(y, y_pred):
- log_loss = -1.0*(w1*t*log(p) + w2*(1-t)*(t*log(1-p))
- return log_loss
附注:您可以很容易地将其扩展到称为交叉熵的多类设置。
Brier分数
当任务本质上是二元分类时，通常使用Brier分数。 它只是实际值和预测值之间的平方差。 对于N组样本，我们将其取平均值。
您可以如下所示进行计算-
- def brier_score(y, y_pred):
- s=0
- for i, j in zip(y, y_pred):
- s += (j-i)**2
- return s * (1/len(y))
在本篇文章中，我们看到了一些流行的评估指标，每个数据科学家在根据手头问题的性质评估机器学习分类模型时都必须牢记这些评估指标。
