之前给大家介绍了几个简单排序,大家只需了解即可,下面介绍的大家就需要熟练掌握了,是面试高频考点,该文章分别用了递归法和迭代法实现 2 路归并,希望对大家有一丢丢的帮助。
归并排序 (Merge Sort)
归并排序是必须要熟练掌握的排序算法,是面试高频考点,下面我们就一起来扒一扒归并排序吧,原理很简单,大家一下就能搞懂。
袁记菜馆内
第 23 届食神争霸赛开赛啦!
袁厨想在自己排名前4的分店中,挑选一个最优秀的厨师来参加食神争霸赛,选拔规则如下。
第一场 PK:每个分店选出两名厨师,首先进行店内 PK,选出店内里的胜者
第二场 PK: 然后店内的优胜者代表分店挑战其他某一分店的胜者(半决赛)
第三场 PK:最后剩下的两名胜者进行PK,选出最后的胜者。
示意图如下
厨神争霸赛
上面的例子大家应该不会陌生吧,其实我们归并排序和食神选拔赛的流程是有些相似的,下面我们一起来看一下归并排序吧。
归并这个词语的含义就是合并,并入的意思,而在我们的数据结构中的定义是将两个或两个以上的有序表合成一个新的有序表。而我们这里说的归并排序就是使用归并的思想实现的排序方法。
归并排序使用的就是分治思想。顾名思义就是分而治之,将一个大问题分解成若干个小的子问题来解决。小的子问题解决了,大问题也就解决了。分治后面会专门写一篇文章进行描述,这里先简单提一下。
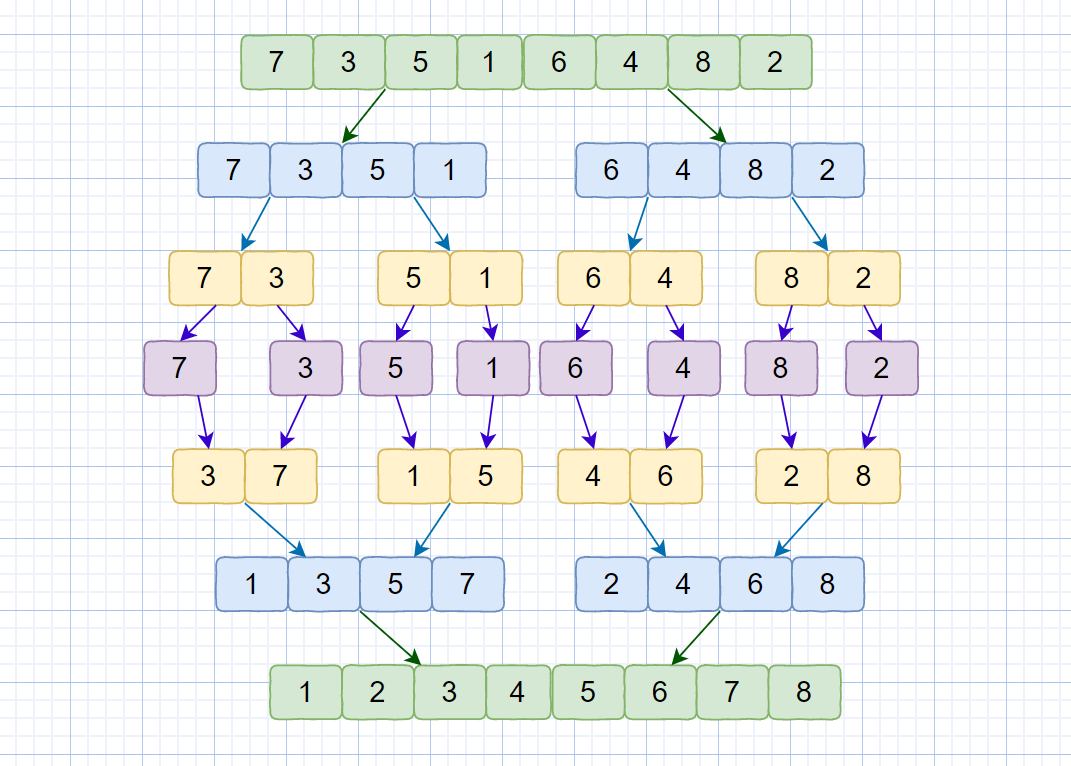
下面我们通过一个图片来描述一下归并排序的数据变换情况,见下图。
归并排序
我们简单了解了归并排序的思想,从上面的描述中,我们可以知道算法的归并过程是比较难实现的,这也是这个算法的重点,我们先通过一个视频来看一下归并函数的具体步骤,看完我们这个视频就能懂个大概啦。
视频中归并步骤大家有没有看懂呀,没看懂也不用着急,下面我们一起来拆解一下,归并过程共分三步走。
第一步:创建一个额外大集合用于存储归并结果,长度则为那两个小集合的和,从视频中也可以看出
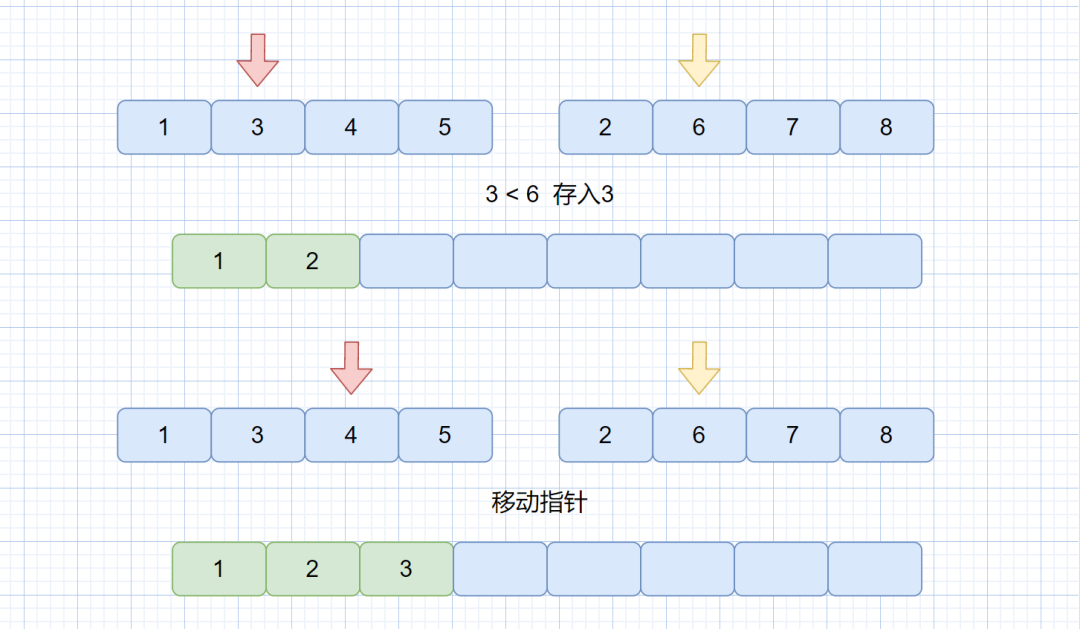
第二步:我们从左自右比较两个指针指向的值,将较小的那个存入大集合中,存入之后指针移动,并继续比较,直到某一小集合的元素全部都存到大集合中。见下图
合并
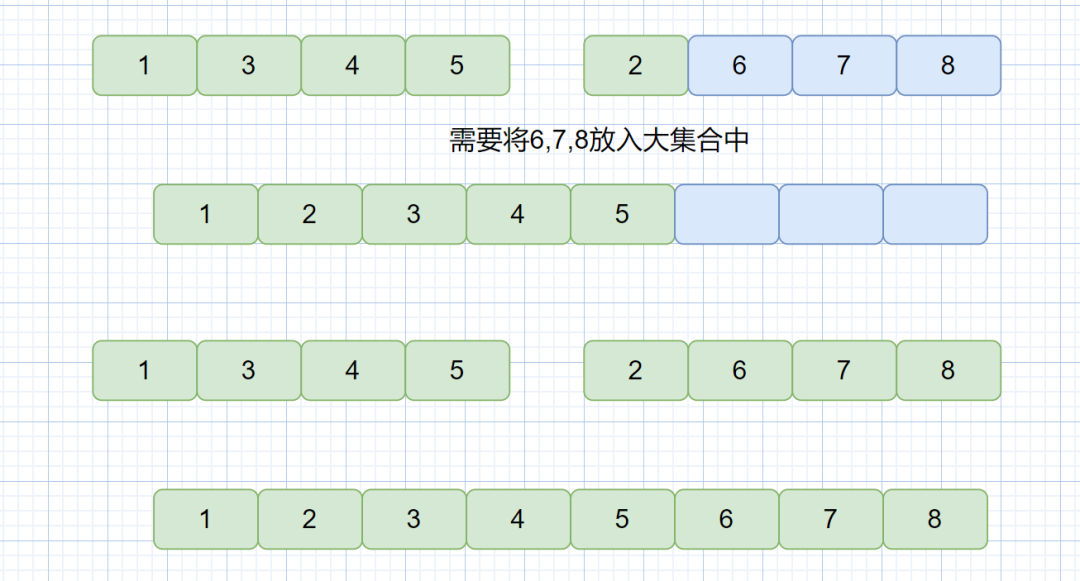
第三步:当某一小集合元素全部放入大集合中,则需将另一小集合中剩余的所有元素存到大集合中,见下图
好啦,看完视频和图解是不是能够写出个大概啦,了解了算法原理之后代码写起来就很简单啦,
下面我们看代码吧。
注:这里用了System.arraycopy(),大家也可以使用其他方法,其中的五个参数分别是,源数组,目的数组,源数组起始索引,目的数组放置的起始索引,复制的长度
- class Solution {
- public int[] sortArray(int[] nums) {
- mergeSort(nums,0,nums.length-1);
- return nums;
- }
- public void mergeSort(int[] arr, int left, int right) {
- if (left < right) {
- int mid = left + ((right - left) >> 1);
- mergeSort(arr,left,mid);
- mergeSort(arr,mid+1,right);
- merge(arr,left,mid,right);
- }
- }
- //归并
- public void merge(int[] arr,int left, int mid, int right) {
- //第一步,定义一个新的临时数组
- int[] temparr = new int[right -left + 1];
- int temp1 = left, temp2 = mid + 1;
- int index = 0;
- //对应第二步,比较每个指针指向的值,小的存入大集合
- while (temp1 <= mid && temp2 <= right) {
- if (arr[temp1] <= arr[temp2]) {
- temparr[index++] = arr[temp1++];
- } else {
- temparr[index++] = arr[temp2++];
- }
- }
- //对应第三步,将某一小集合的剩余元素存到大集合中
- if (temp1 <= mid) System.arraycopy(arr, temp1, temparr, index, mid - temp1 + 1);
- if (temp2 <= right) System.arraycopy(arr, temp2, temparr, index, right -temp2 + 1);
- System.arraycopy(temparr,0,arr,0+left,right-left+1);
- }
- }
归并排序时间复杂度分析
我们一趟归并,需要将两个小集合的长度放到大集合中,则需要将待排序序列中的所有记录扫描一遍所以时间复杂度为O(n)。
归并排序把集合一层一层的折半分组,则由完全二叉树的深度可知,整个排序过程需要进行 logn(向上取整)次,则总的时间复杂度为 O(nlogn)。
另外归并排序的执行效率与要排序的原始数组的有序程度无关,所以在最好,最坏,平均情况下时间复杂度均为 O(nlogn) 。
虽然归并排序时间复杂度很稳定,但是他的应用范围却不如快速排序广泛,这是因为归并排序不是原地排序算法,空间复杂度不为 O(1),那么他的空间复杂度为多少呢?
归并排序的空间复杂度分析
归并排序所创建的临时结合都会在方法结束时释放,单次归并排序的最大空间是 n ,所以归并排序的空间复杂度为 O(n).
归并排序的稳定性分析
归并排序的稳定性,要看我们的 merge 函数,我们代码中设置了 arr[temp1] <= arr[temp2] ,当两个元素相同时,先放入arr[temp1] 的值到大集合中,所以两个相同元素的相对位置没有发生改变,所以归并排序是稳定的排序算法。
等等还没完嘞,不要走呀。
归并排序的递归实现是比较常见的,也是比较容易理解的,下面我们一起来扒一下归并排序的迭代写法。看看他是怎么实现的。
我们通过一个视频来了解下迭代方法的思想
是不是通过视频了解个大概啦,下面我们来对视频进行解析。
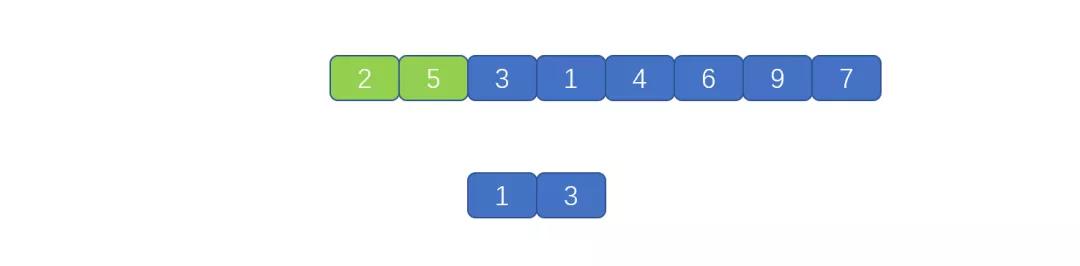
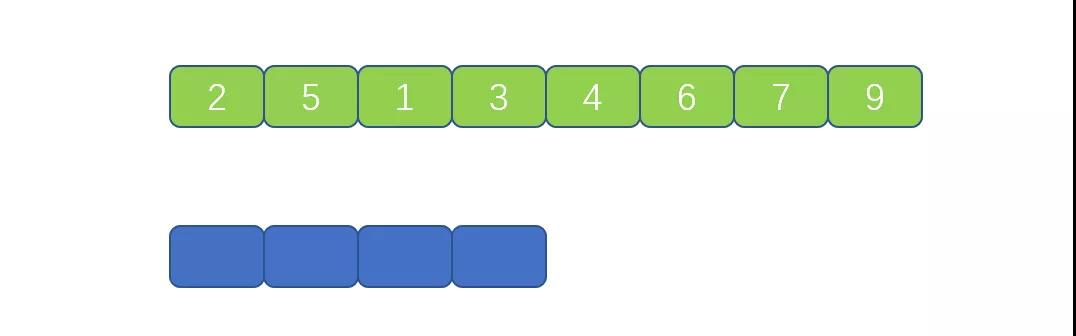
迭代实现的归并排序是将小集合合成大集合,小集合大小为 1,2,4,8,…..。依次迭代,见下图
比如此时小集合大小为 1 。两个小集合分别为 [3],[1]。
然后我们根据合并规则,见第一个视频,将[3],[1]合并到临时数组中,则小的先进,进而实现了排序,然后再将临时数组的元素复制到原来数组中。则实现了一次合并。
下面则继续合并[4],[6]。具体步骤一致。所有的小集合合并完成后,则小集合的大小变为 2,继续执行刚才步骤,见下图。
此时子集合的大小为 2 ,则为 [2,5],[1,3] 继续按照上面的规则合并到临时数组中完成排序。这就是迭代法的具体执行过程,
下面我们直接看代码吧。
注:递归法和迭代法的 merge 函数代码一样。
- class Solution {
- public int[] sortArray (int[] nums) {
- //代表子集合大小,1,2,4,8,16.....
- int k = 1;
- int len = nums.length;
- while (k < len) {
- mergePass(nums,k,len);
- k *= 2;
- }
- return nums;
- }
- public void mergePass (int[] array, int k, int len) {
- int i;
- for (i = 0; i < len-2*k; i += 2*k) {
- //归并
- merge(array,i,i+k-1,i+2*k-1);
- }
- //归并最后两个序列
- if (i + k < len) {
- merge(array,i,i+k-1,len-1);
- }
- }
- public void merge (int[] arr,int left, int mid, int right) {
- //第一步,定义一个新的临时数组
- int[] temparr = new int[right -left + 1];
- int temp1 = left, temp2 = mid + 1;
- int index = 0;
- //对应第二步,比较每个指针指向的值,小的存入大集合
- while (temp1 <= mid && temp2 <= right) {
- if (arr[temp1] <= arr[temp2]) {
- temparr[index++] = arr[temp1++];
- } else {
- temparr[index++] = arr[temp2++];
- }
- }
- //对应第三步,将某一小集合的剩余元素存到大集合中
- if (temp1 <= mid) System.arraycopy(arr, temp1, temparr, index, mid - temp1 + 1);
- if (temp2 <= right) System.arraycopy(arr, temp2, temparr, index, right -temp2 + 1);
- //将大集合的元素复制回原数组
- System.arraycopy(temparr,0,arr,0+left,right-left+1);
- }
- }
通过上面的视频解析和代码,希望大家能够将归并排序给拿下,下面会给大家写一下,归并排序在实际刷题时的应用,感谢阅读。
本文转载自微信公众号「袁厨的算法小屋」,可以通过以下二维码关注。转载本文请联系袁厨的算法小屋 公众号。