本质栈是一种特殊的数据结构,它特殊在它的结构,与数组、链表不同的是,它的数据出入规则是:先进后出,后进先出。
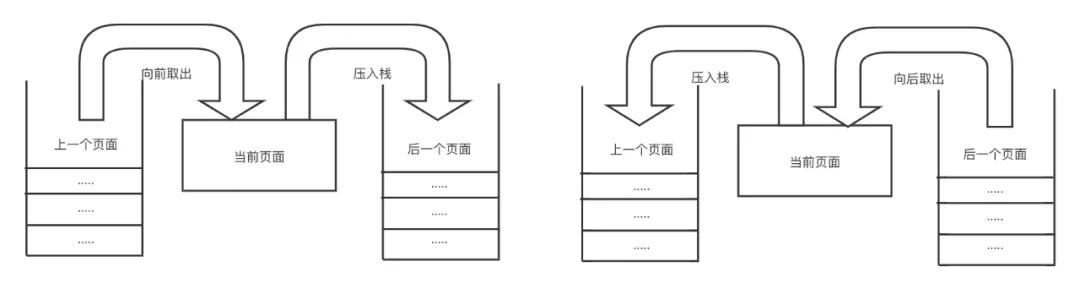
由于它这种特殊的特性,它一般用于指定的场景之下,例如:浏览器的前进与回退效果。
浏览器的特性是:我们可以向前访问我们之前访问的网站,也可以向后访问后面的网站。
浏览器的这种特性,完美匹配了栈的结构。
我们只需使用两个栈,分别代表浏览器的向前访问与向后访问。
当某个数据集合只涉及在一端插入和删除数据,并且满足先进后出,后进先出的特性,这时我们应该首先想到的是栈,看它是否能够更好的实现我们所需的场景。
实现方式栈的实现方式有两种,一种是基于数组的实现方式,称为顺序栈;另一种是基于链表的实现方式,称为链式栈。
这两种实现方式区别不是很多,实现之后栈的出入时间复杂度都是O(1)。
不同的是基于数组实现的栈消耗的内存更少,因为它不需要额外保存指向的指针。
但基于数组的另外一额外需要做的是,如果需要实现不定大小的栈,它需要实现动态扩容,这是所有基于数组实现的一个必修课。
下面我们来实现一个基于数组的顺序栈,为了减少复杂度,不考虑扩容的情况。
// 基于数组实现的顺序栈class ArrayStack(private val n: Int) { private val items = arrayOfNulls
基于上面的实现,我们能够很容易得出栈的出入时间复杂度为O(1)。
另一方面,由于没有额外的空间申请,所以栈的空间复杂度为O(1)。
扩容上面我们实现的是一个固定的顺序栈,也就是说初始化的时候已经指定了栈的大小,当栈满了的时候,无法进行向栈中添加数据。当然基于链表的链式栈没有这种限制。
为了解决顺序栈的这种限制,我们需要对数据进行扩容操作,这在数组那一节也有提及过。
所以,如果要实现一个支持扩容的栈,我们只需底层依赖一个基于扩容的数组即可。
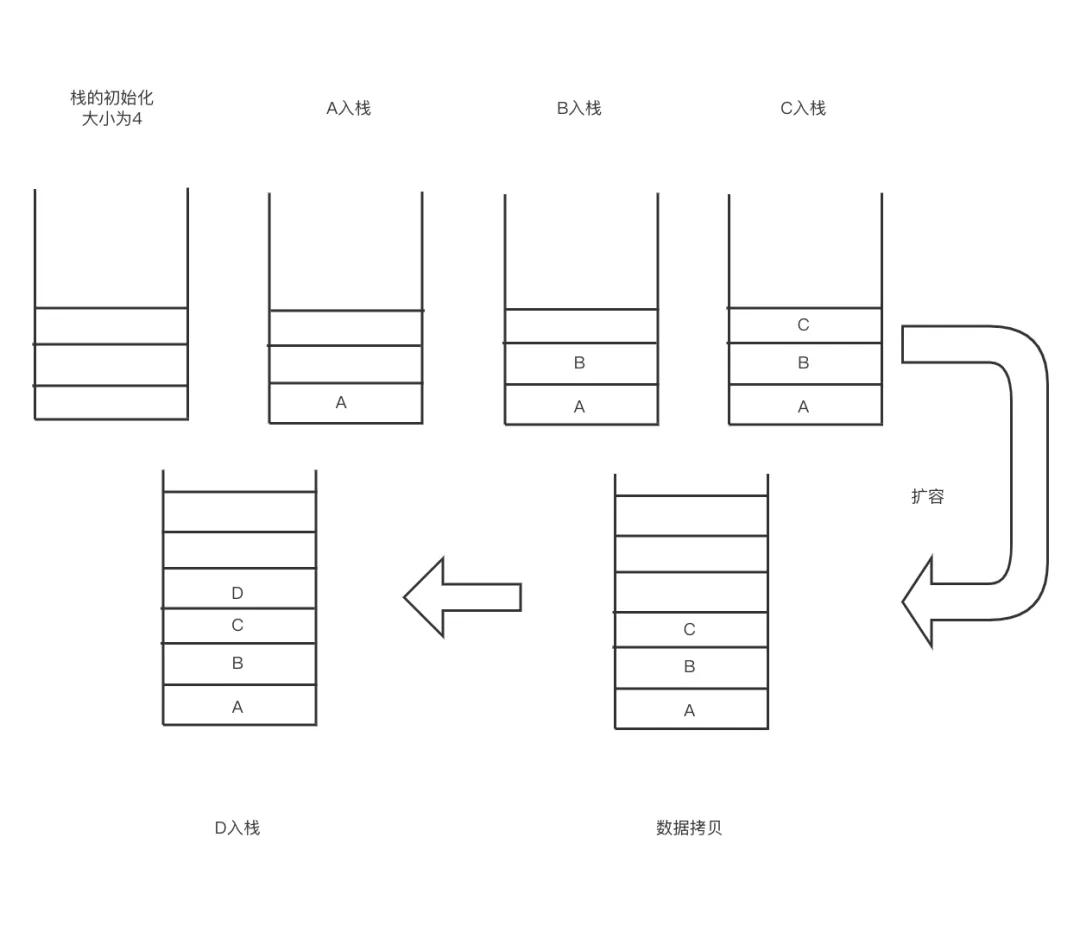
具体的扩容示意图如下:
具体代码实现可以查看数据的扩容。
下面我们再来分析一下基于数组扩容的栈的时间复杂度。
首先未达到栈的大小时,这一阶段与固定的顺序栈一样,出入的时间复杂度都为O(1)。
当数据为K时且达到扩容的临界点时,需要将数组的大小扩大到原来的两倍,并将之前的数据拷贝的新的数组中;这一阶段消耗的时间复杂度为O(K)。
当扩容结束之后继续出入栈,此时的时间复杂度又为O(1)。
当再一次达到2k时又需要再次扩容,拷贝数据到新数组中,此时消耗的时间复杂度为O(2k)。
反复重复以上步骤。
这就是支持扩容的顺序栈的时间复杂度的变化。也就是说最好情况的时间复杂度为O(1);最坏的时间复杂度为O(n)。那么平均时间复杂度呢?
还记得在算法之旅:复杂度分析中提到的均摊时间复杂度吗?
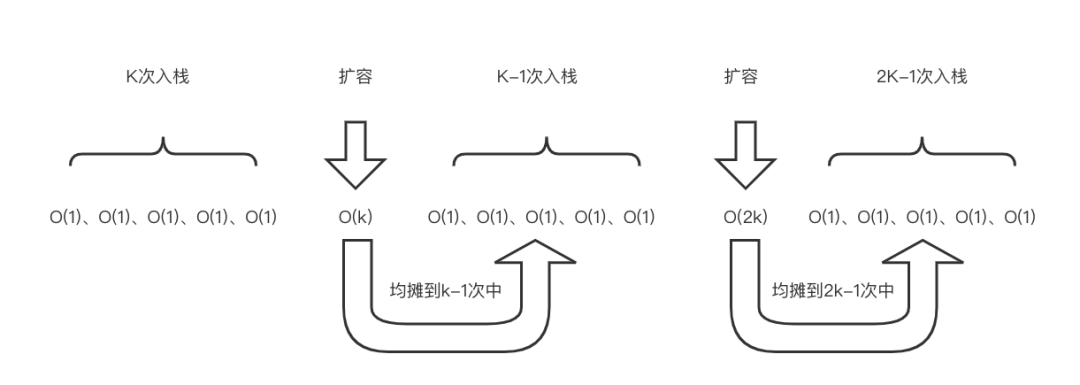
下面我们就利用均摊时间复杂度来分析它的平均时间复杂度。其实看一张图就能够明白均摊时间复杂度的算法。
每次我们都将扩容的所消耗的时间都分摊到之后的入栈中。在分摊之前入栈需要一个push的时间;分摊之后入栈在push的时间上再加上一个数据move的时间。push与move的时间复杂度都为O(1)。
所以均摊之后栈的整个时间复杂度就是O(1),即栈的平均复杂度为O(1)。
栈的应用现在我们已经对栈有了一个全面的了解,为了完全巩固栈这种数据结构,我们剩下的就是练习以达到熟悉程度。
例如:实现一个基本的计算器来计算一个简单的字符串表达式的值, 字符串表达式可以包含左括号(,右括号),加号+,减号-,非负整数和空格。
基于表达式的运算,非常符合栈这种结构,我们可以使用栈来实现的。实现思路如下:
通过设定一个符号位将所有的运算转化成加法
遇到数字都带上之前的符号位,再与之前的结果做加法运算
遇到'('将之前的符号位与结果保留到栈中,然后再重复1 2步骤计算括号里面的值
遇到')'取出之前保留的符号位与结果,与当前结果做加法运算
/** * O(n) */fun calculate(s: String): Int { val numberStack = Stack
还有一些关于栈的经典练习,如果能够掌握这些,那么有关栈的算法就基本没什么问题了
比较含退格的字符串
棒球比赛
下一个更大元素
有效的括号
我将源码放在Github上了,如有需要的可以自行查看。
本文转载自微信公众号「 Android补给站」,可以通过以下二维码关注。转载本文请联系 Android补给站公众号。