背景
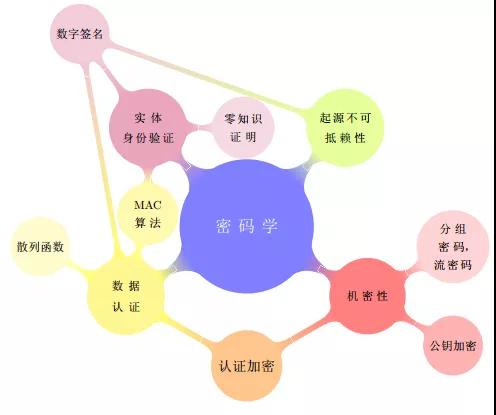
在1949年,Shannon的The mathematical theory of communication [9]是现代密码学的理论基础,也标志着密码算法的重心向应用数学上的转移。文中提出分组密码算法应该遵循混淆(Confusion)和扩散 (Diffusion)两大准则,密码体制的完善保密性, ”乘积”密码体制 。其中”乘积”密码体制对Feistel之后提出Feistel密码结构具有指导意义。柯克霍夫原则 (Kerckhoffs Principle)[7]由Kerckhoffs在19世纪提出:即使密码系统的任何细节已为人悉知,只要密匙(key,又称密钥或秘钥)未泄漏,它也应是安全的 。Shannon 有句近似的话: 敌人知道系统,称为香农公理。密码学中公钥密码和对称密码用来保护数据的机密性,如图1。
图1 密码学
公钥密码:Whitefield与Martin Hellman在1976年[4]提出了Diffie-Hellman密钥交换协议/算法 (Diffie-Hellman Key Exchange/Agreement Algorithm),公钥密码开始发展。公钥密码是运用陷门单向函数原理编制的加密密钥公开,解密密钥保密的密码。公钥密码的安全性理论基础是计算复杂性理论。公钥密码的安全性指计算安全性,通常是基于特定数学难题的计算困难性而设计的,主要有大整数因子分解的困难性,有限域上离散对数的难解性,椭圆曲线加法群上离散对数的难解性等。第一个比较完善的公钥密码算法是Rivest、Shamir和 Adleman在1978年提的RSA[8]公钥密码算法,它的安全性基础是大整数因子分解的困难性。对称加密:对称密码与公钥密码体制相比,对称密码算法算法简单,效率高,适合加密大量数据。对称加密算法指加密和解密使用相同密钥。对称加密算法的安全性取决于加密密钥的安全性。对称加密算法的优点在于加解密的高速度和使用长密钥时的难破解性。对称密码根据对明文加密方式的不同,可分为:流密码和分组密码。
分组密码
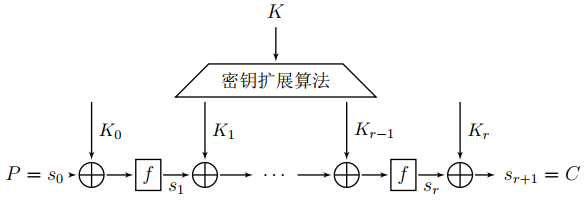
分组密码 (block cipher) 的数学模型是将明文消息按分组密码的分组长度划分成定长的信息块,每个信息块分别在密钥的控制下变换成等长的输出消息。对称密码算法的轮函数f都包含子密钥操作,线性操作,非线性操作3部分。其中非线性操作主要混淆,线性操作主要扩散。通过将轮函数f多次迭代 (图 2 ) 达到高安全强度。分组密码易于软硬件实现且不需要同步,因此在现代密码产品和分组交换网络中有着广泛的应用。
图2 分组密码算法
对称密码算法都是基于以下两种本原操作:
1.混淆 (Confusion): 是一种使密钥与密文之间的关系尽可能模糊的加密操作;2.扩散 (Diffusion): 是一种为了隐藏明文的统计特性而将一个明文符号的影响扩散到多个密文符号的加密操作。按照算法结构的不同,分组密码可以分为两类:Feistel 结构、SPN 结构。
Feistel 结构
Feistel 结构的分组密码:令F为轮函数;令K1,K2,……,Kn 分别为第1,2,……,n轮的子密钥。那么基本构造过程如下:
1. 将明文信息均分为两块:(L0, R0);2. 在每一轮中,进行如下运算(为当前轮数):Li+1=Ri;Ri+1=Li ⊕ F(Ri,Ki);
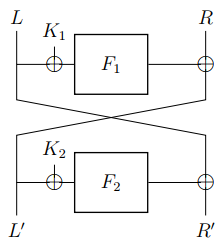
Feistel结构(图3)一次仅一半的数据进入F函数,它的优点在于:由于它是对称的密码结构,所以加密和解密过程就极为相似,只有密钥使用方式不同。Feistel结构的优势在于加解密方式相同、节省资源;缺点是扩散速度低,为达到一定的安全性通常需要迭代更多的轮数。Feistel结构代表算法有DES算法、ISO/IEC 国际标准算法Camellia、Blowfish、日本NTT公司的DES算法在软件应用方面的后补 FEAL算法、以及我国的商业分组密码标准 SM4 等。
图3 Feistel结构
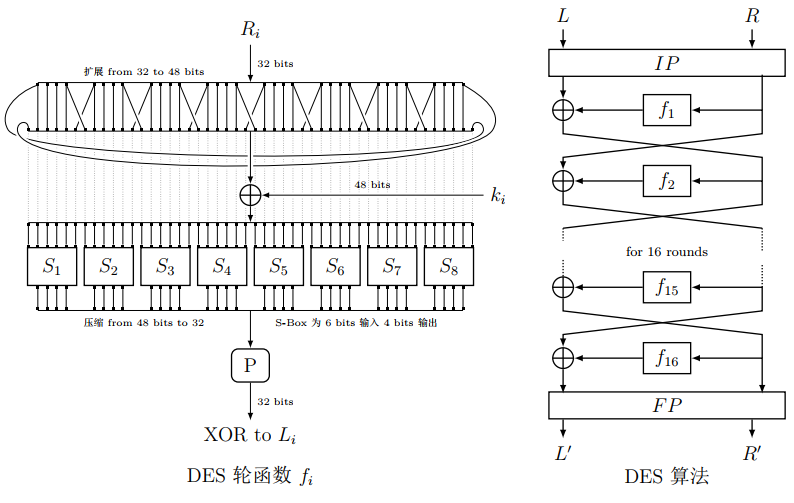
DES(Data Encryption Standard,即数据加密标准)是一种使用密钥加密的分组密码算法,1977年被美国联邦政府的国家标准局确定为联邦资料处理标准 (FIPS),并授权在非密级政府通信中使用,随后该算法在国际上广泛流传开来。DES设计中使用了密码算法设计的两个原则:混淆和扩散,使用乘积密码的概念来逼近理想分组密码,其目的是抗击敌手对密码系统的统计分析 [10],包括Kasiski 测试法和重复指数法 。由于DES分组比较短、密钥短、运算速度较慢等自身原因,以及计算机计算能力的提升,线性分析[5]和差分分析[1]等分析方法的发展,DES的安全性受到了极大地威胁。3DES(即Triple DES) 是 DES向AES过渡的加密算法,它使用2个56位的密钥对数据进行三次加密,密钥长度变成 112位,加密的过程是加密-解密-加密,解密的过程是解密-加密-解密,比起最初的 DES,3DES更为安全。
图4 DES算法
代换-置换网络 (Substitution-Permutation Network,SPN) 结构
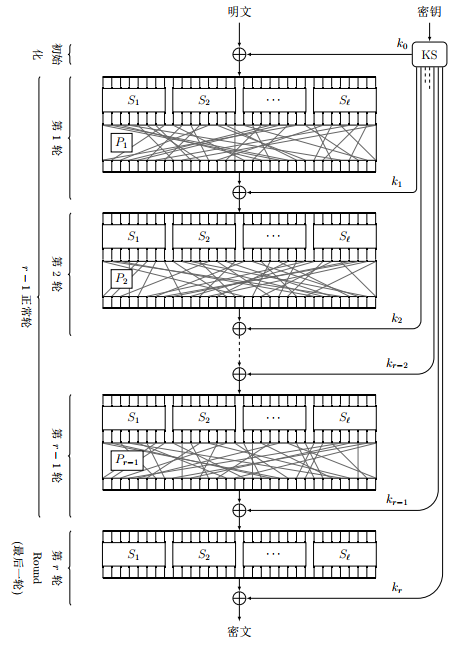
SPN结构(图5)的密码算法一次处理全部的数据。相同长度的分组密码算法,SPN结构与Feistel 结构的F轮函数相比,Feistel结构的F函数处理的数据长度为SPN结构的F函数的一半。SPN结构相较于Feistel结构具有更好的扩散性;但加解密不对称造成了一定程度的实现资源浪费。SPN结构的代表算法包括AES、Serpent、韩国加密标准ARIA等。
图5 代换-置换网络 (Substitution-Permutation Network,SPN)结构
在1991年E Biham和A Shamir提出差分分析[1],1994年Matsui提出线性分析[5]之后,同样伴随计算机计算能力的不断提升,分组长度为64bit和16轮异或、置换、代换、移位的Feistel结构的DES不能保证足够的安全。1997年4月15日,美国ANSI发起征集AES(advanced encryptionstandard) [3] [11]的活动,旨在寻找替代DES的对称加密算法,比利时密码学家Joan Daemen和Vincent Rijmen提出的Rijndael成为获胜者,Rijndael使用的是SPN结构,基于宽轨迹策略 (wide trail strategy)设计,能够很好的抵抗差分密码分析及线性密码分析。AES的非线性部件为具有较好的差分传播性质的8比特S盒,线性部件通过小MDS矩阵与置换组合实现大MDS 矩阵达到最佳扩散。高级加密标准 (Advanced Encryption Standard,AES)[2]由美国国家标准与技术研究院(NIST)于2001年11月26日发布于FIPS PUB 197[6],并在2002年5月26日成为有效的标准。2006 年,高级加密标准已然成为对称密钥加密中最流行的算法之一。AES在软件及硬件上都能快速地加解密,易于实现,且只需要很少的存储器。
图6 SPN结构的密码算法
注解:
(1)乘积密码指顺序地执行两个或多个基本密码系统,使得最后结果的密码强度高于每个基本密码系统产生的结果。
(2)乘积密码指顺序地执行两个或多个基本密码系统,使得最后结果的密码强度高于每个基本密码系统产生的结果。
(3) Kerckhoffs Principle states that the security of a cryptosystem must lie in the choice of its keys only; everything else (including the algorithm itself) should be considered public knowledge。
(4)Kasiski 测试法 [10] 思路是对一份用周期性多表密码加密的密文,确定其中所有的重复出现的字母串,计算他们之间的距离,并对这些距离进行因子分解,出现频率较高的因子很可能是密钥的长度。
(5)重复指数法 [10] 利用随机文本和英文文本的统计概率差别来分析密钥长度。
参考文献:
[1] Eli Biham and Adi Shamir. Differential cryptanalysis of des-like cryptosystems. In Advances in Cryptology - CRYPTO ’90, 10th Annual International Cryptology Conference,Santa Barbara, California, USA, August 11-15, 1990, Proceedings, 1991.
[2] J Daemen. Aes proposal : Rijndael, aes algorithm submission.
http://www.nist.gov/CryptoToolkit, 1999.
[3] Joan Daemen, Vincent Rijmen, and Katholieke Universiteit Leuven. Aes proposal:Rijndael. 1998.
[4] W. Diffie and M. Hellman. New directions in cryptography. IEEE Transactions on Information Theory, 22(6):644–654, 1976.
[5] Mitsuru Matsui. Linear cryptanalysis method for des cipher (iii). In Workshop on the theory and application of cryptographic techniques on Advances in cryptology, 1995.
[6] National Institute of Standards and Technology. Advanced encryption standard (aes). https://csrc.nist.gov/publications/detail/fips/197/final, 2001.
[7] Fabien A. P. Petitcolas. Kerckhoffs’ Principle, pages 675–675. Springer US, Boston,
MA, 2011.
[8] R. L. Rivest, A. Shamir, and L. Adleman. A method for obtaining digital signatures and public-key cryptosystems. Communications of the Acm, 21(2):120–126, 1978.
[9] C. E. Shannon. The mathematical theory of communication. Bell Labs Technical Journal, 3(9):31–32, 1950.
[10] M Stamp and R Low. Applied Cryptanalysis: Breaking Ciphers in the Real World. Wiley-Interscience, 2007.
[11] Sam Trenholme. The aes encryption algorithm. https://www.samiam.org/rijndael.html.