本文转自雷锋网,如需转载请至雷锋网官网申请授权。
广度优先搜索、Dijkstra和A*是图上的三种典型路径规划算法。它们都可用于图搜索,不同之处在于队列和启发式函数两个参数。
本项目探索并可视化不同算法如何根据选择参数进行图搜索。
算法的一般性原理如下:
将边界初始化为包含起始节点的队列。
当边界队列不为空时,从队列中“访问”并删除一个“当前”节点,同时将访问节点的每个邻居节点添加到队列,其成本是到达当前节点的成本加上从当前节点访问邻居的成本再加上邻居节点和目标节点的启发式函数值。其中,启发式函数是对两个节点的路径成本的估计。
存储访问路径(通常存储在cameFrom图中),以便后续重建路径。如果邻居节点已经在列表中,同时新路径的成本较低,那么更改其成本。
找到目标路径(提前退出)或列表为空时,停止算法。
BFS
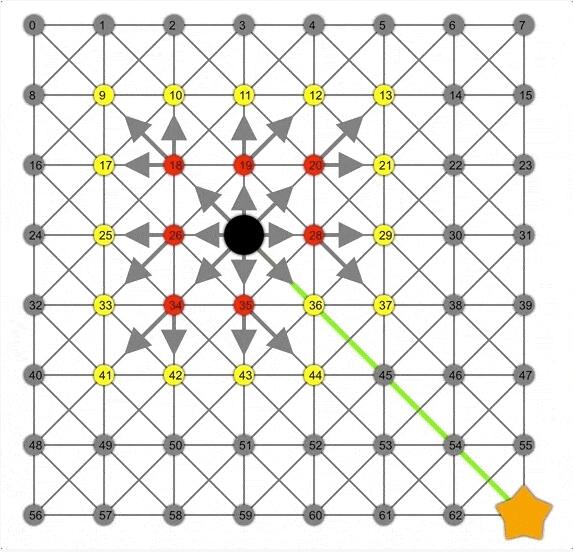
使用先进先出队列实现BFS。这种队列会忽略路径中链接的开销,并根据跳数进行扩展,因此可以确保找到最短路径的跳数,而跳数相关的成本。启发式函数的选择是任意的,因为在这个过程中其并不起作用。
使用数组可实现先进先出,即将元素附加到末尾并从头删除。
BFS演示动图。注意边界节点(黄色)是如何在网格中扩展为正方形的。在这里,正方形是相同“跳距”的节点集。
Dijkstra
在图上使用优先级队列和始终返回0的启发式函数,便得到Dijkstra算法。
相比于BFS,Dijkstra最大的不同在于考虑了成本。通过该算法,可以根据节点到节点的成本找到最短路径。
优先级队列使用数组实现,在每次插入新节点后对该数组进行排序。尽管实现优先级队列还有其他更高效的方式,但在我们的场景中,数组是足够快的,而且实现起来也简单。
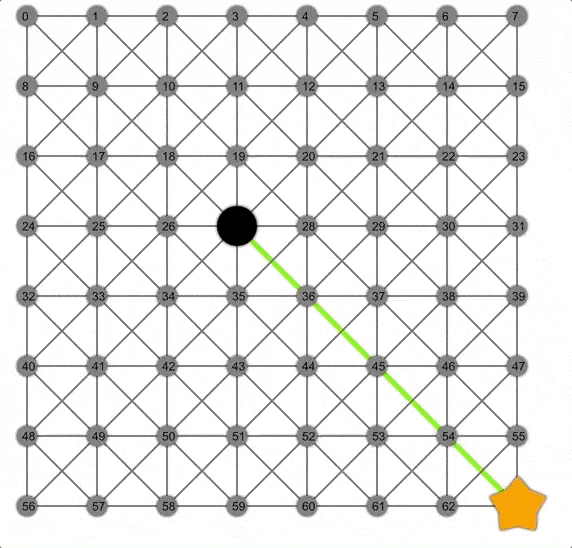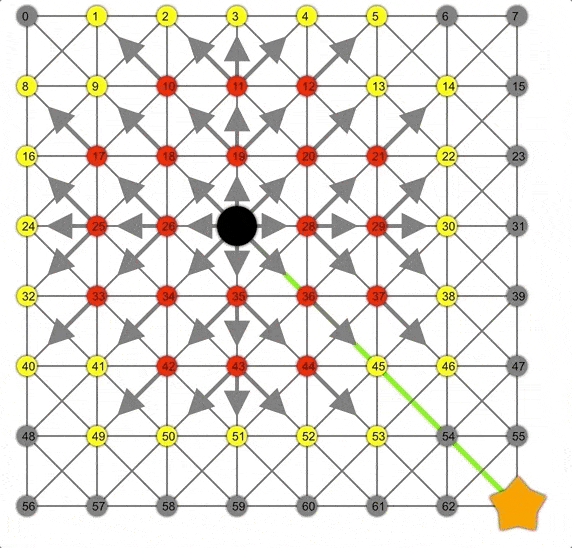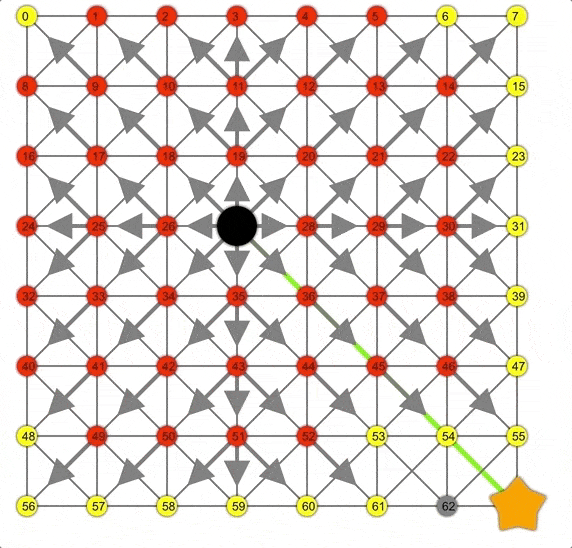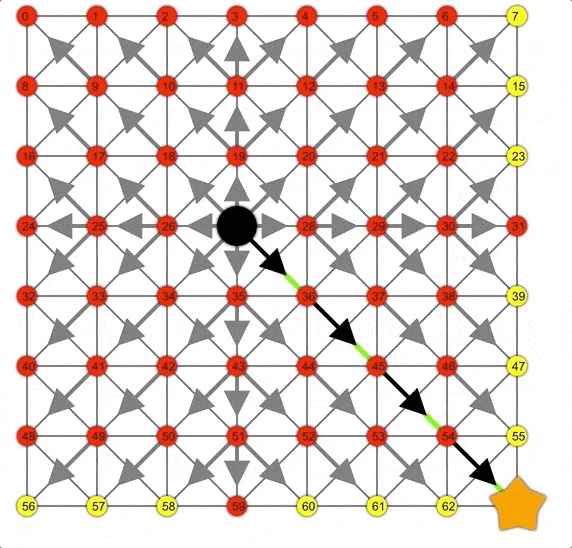
Dijkstra展示动画,注意此时的边界是一个圆。
A*
为实现A*算法,需要传递一个实际启发式函数,例如两个节点之间的欧式距离。通过“节点成本”+“节点到目标节点的估算成本”对节点进行加权,通过优先搜索更大可能的节点加快搜索速度。
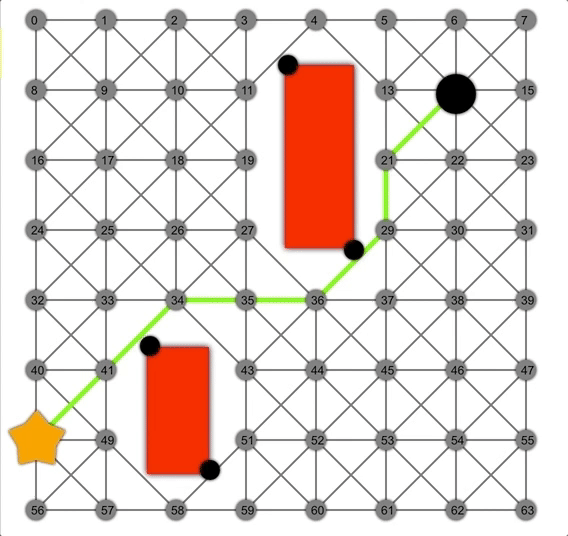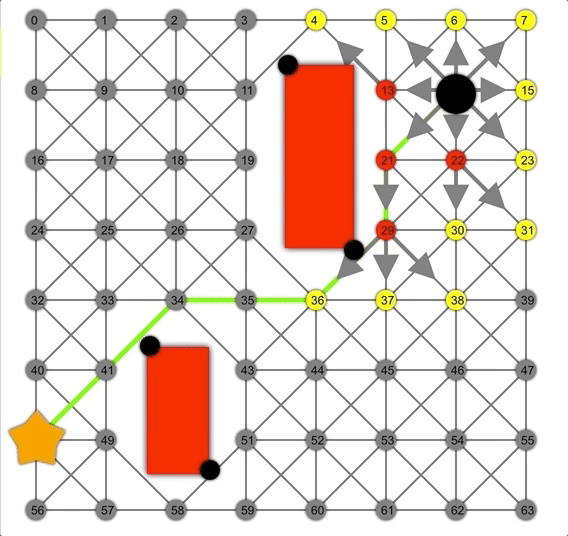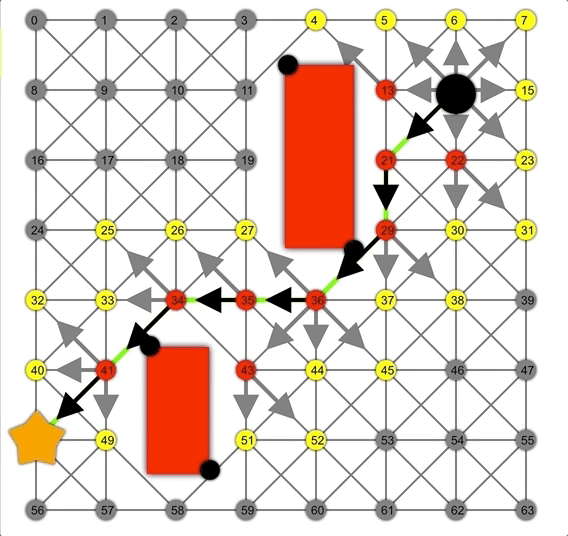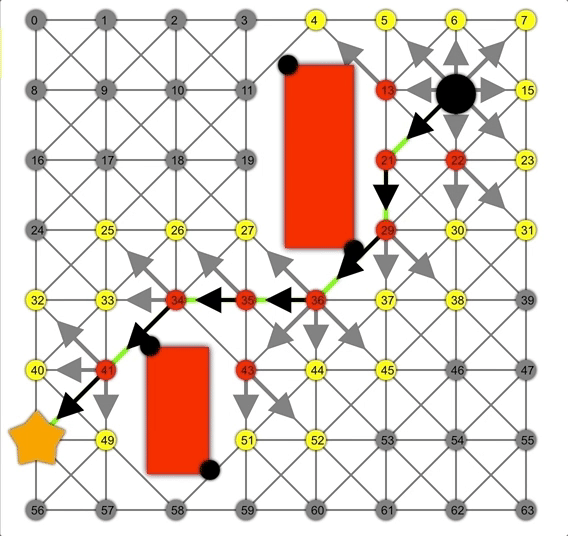
借助启发式方法,A*可以比Dijkstra或BFS更快地找到正确路径。
非允许的启发式函数
只有应用可允许启发式函数,A*才能找到最短路径,这也意味着算法永远不会高估实际路径长度。由于欧氏距离是两点之间的最短距离/路径,因此欧氏距离绝不会超出。
但如果将其乘以常数k>0会怎样呢?这样会高估距离,成为非允许的启发式函数。
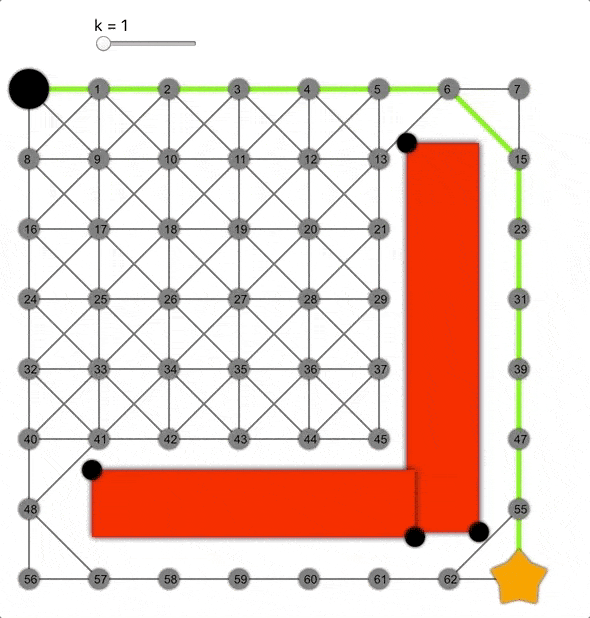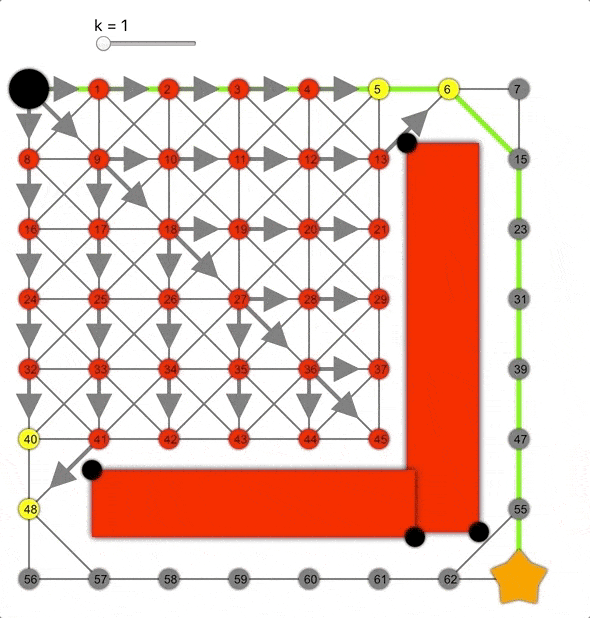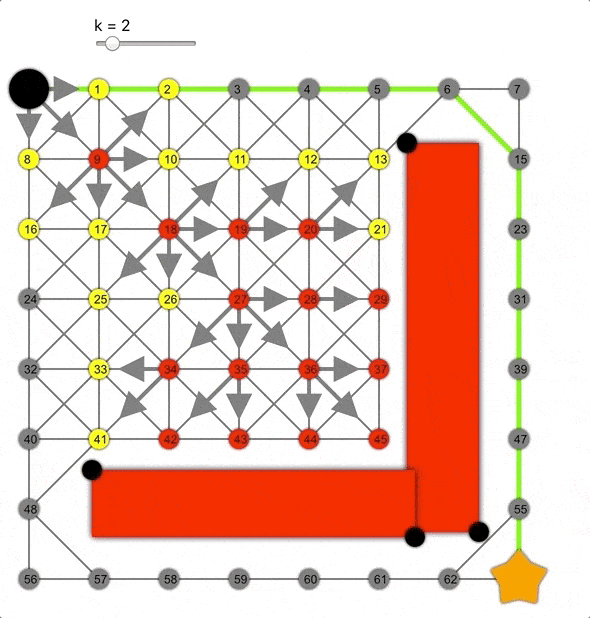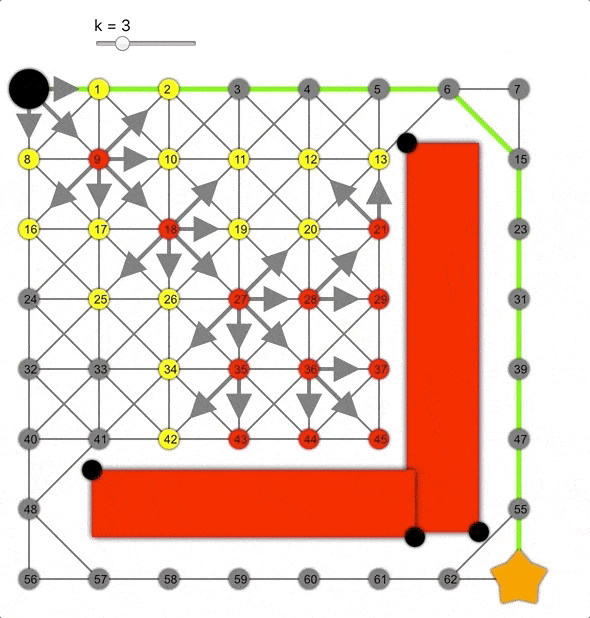
k值越大,算法越容易到达目标,但同时准确性降低,导致生成的路径并非总是最短的。
算法实现
本项目通过Javascript实现,以便读者在Web上进行访问。另外,我使用react渲染UI,使用react-konva渲染图形。
路径发现是指接受队列类型和启发式函数,并返回另一个函数,即真实路径发现(称为currying)。
这样,用户每次更改设置后,都会使用确定参数创建一个新的路径发现函数,并将之用于图搜索。
为可视化路径发现的步骤,我使用javascript生成器,这意味着函数返回一个迭代器,而不仅仅是一个值。因此,访客在每一步都可以生成算法的整个状态,并将其保存到数组,然后通过页面顶部的滑块显示特定状态。
此链接进入交互演示页面:https://interactive-pathfinding.netlify.com/