前言
今天继续算法题:从尾到头打印链表
链表
在看今天题目之前,我们先了解下链表。
链表是一种物理存储单元上非连续、非顺序的存储结构。由于不必须按顺序存储,链表的插入和删除操作可以达到O(1)的复杂度
熟悉数组的都知道,数组是需要一块连续的内存空间来存储。而链表就不需要,它是通过指针来将内存块串联起来。
常见的链表结构有:单链表、双向链表和循环链表。(图片来自参考链接)
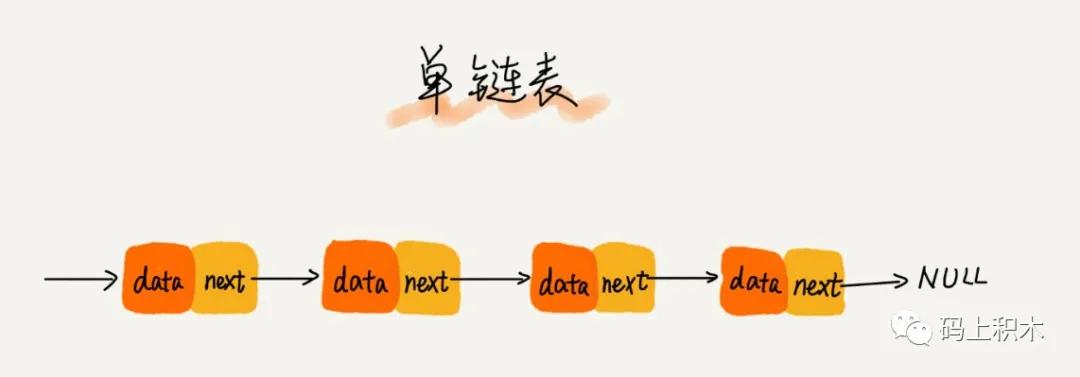
单链表
第一个接点为头结点,最后一个结点是尾结点。
从图中可以看出来:当某个结点不是指向下一个结点,而是指向了null,空地址,那么这个结点就是这个链表最后一个结点,也就是尾结点。
当我们插入或者删除结点只需要修改next结点就行,也就是修改next指针指向地址,比如这样一个链表:
- a->next=b, b->next=c, c->next=d
a下一个结点是b,b下一个结点是c...
如果我们要在ab直接插入一个结点p,得益于链表的不连续性,我们只需要修改a的next为p,p的next为b就行了。
- a->next=p, p->next=b, b->next=c, c->next=d
通俗点说,插入的时候,就修改两个结点的跟屁虫就行啦。所以不同于数组插入和删除操作,链表的插入和删除效率很高,不需要考虑空间连续问题,所以对应的时间复杂度是O(1)。
但是反过来,如果要查询第n个数据为谁,这个就比较麻烦了。不像数组由于内存连续,所以很轻易就知道n对应的数据。而链表需要一个个next查找,所以链表随机访问的效率就不如数组了,时间复杂度为O(n)。
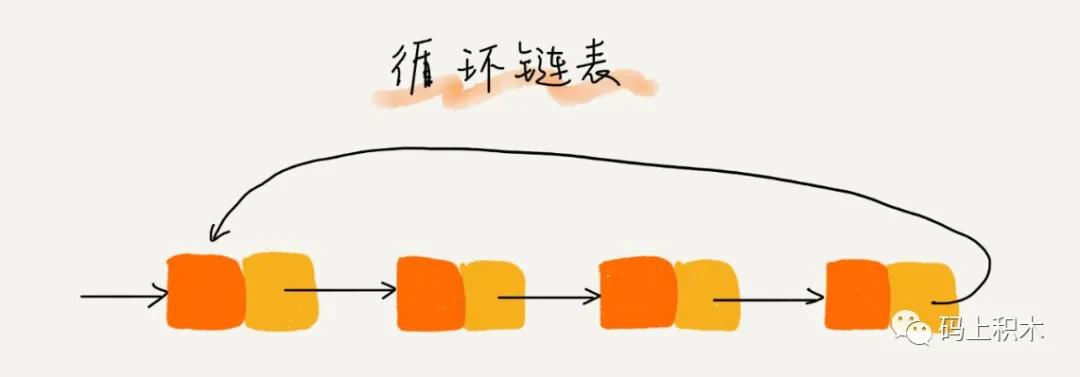
循环链表
循环链表和单链表的区别就是,尾结点指针会指向头结点,形成一个环形,这就是循环链表。
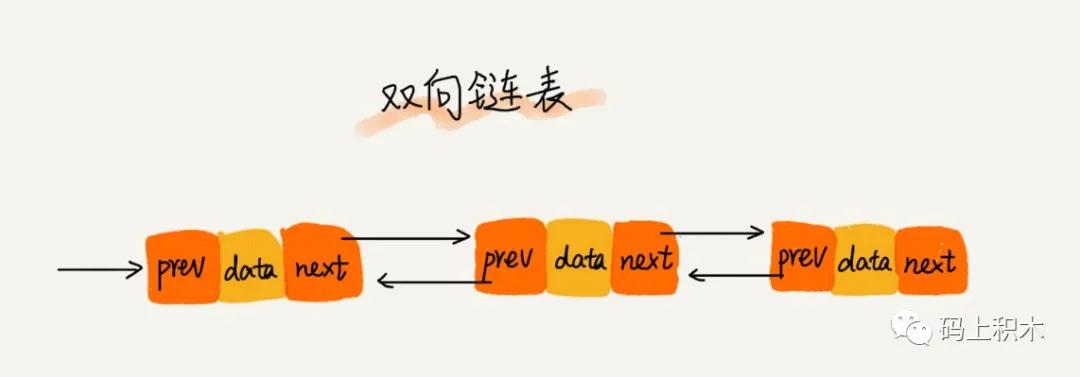
双向链表
如图所示,双向链表和单链表的区别就是,每个结点不仅有下个结点的地址,还有上一个结点的地址。
这样有什么好处呢?在特定的情境中能提高效率。比如我要在某个结点B的前面插入数据,那么我需要从头开始便利,找到某个结点的next指向这个B的地址,然后进行数据的插入。
但是双向链表则可以直接获知结点B的前驱结点地址,大大提高了插入效率。
链表的基础知识就介绍到这里了,下面看一个链表相关的算法题。
题目:从尾到头打印链表
输入一个链表的头节点,从尾到头反过来返回每个节点的值(用数组返回)。
示例 1:
输入:head = [1,3,2] 输出:[2,3,1]
限制:
0 <= 链表长度 <= 10000
解法一
题目意思很简单,就是一个链表,现在要先从尾巴倒着打印链表的数字。
那我们就可以想到可以用到递归算法,递归算法其实就是两步,先递后归,我们可以先传递到链表的最后一位,也就是next->null为空的时候,然后开始归档把数据依次输出,即完成了从结尾开始输出数字的需求了。
- 递推阶段:走到链表结尾为结束的标志。
- 归档阶段:从结尾处一层层输出数字,先输出到ArrayList,在转为数组。
不明白的可以看看代码:
- class Solution {
- ArrayList<Integer> tmp = new ArrayList<Integer>();
- public int[] reversePrint(ListNode head) {
- recur(head);
- int[] res = new int[tmp.size()];
- for(int i = 0; i < res.length; i++)
- res[i] = tmp.get(i);
- return res;
- }
- //递归方法
- void recur(ListNode head) {
- //到链表结尾处,递推结束,开始归档,依次输出
- if(head == null) return;
- recur(head.next);
- tmp.add(head.val);
- }
- }
方法消耗情况
- 执行用时:1 ms
- 内存消耗:40.5 MB
时间复杂度
该算法相当于遍历了两遍链表,递推一遍,归档一遍,所以一共为2n。
去除常量,时间复杂度就是O(n)
空间复杂度
由于用到ArrayList和数组,所以空间复杂度也是O(n)。
解法二
第二种解法就是利用栈的特点:先入后出。(栈的知识点后面再细说)
先入后出不就是题目的需求么,从尾部倒着输出数字。
所以我们把链表依次入栈,然后在依次出栈就可以完成需求了。
- class Solution {
- public int[] reversePrint(ListNode head) {
- LinkedList<Integer> stack = new LinkedList<Integer>();
- while(head != null) {
- stack.addLast(head.val);
- head = head.next;
- }
- int[] res = new int[stack.size()];
- for(int i = 0; i < res.length; i++)
- res[i] = stack.removeLast();
- return res;
- }
- }
方法消耗情况
- 执行用时:1 ms
- 内存消耗:39.2 MB
时间复杂度
同上一个算法一样,时间复杂度就是入栈和出栈的时间,也就是O(n)。
空间复杂度
由于用到了stack和数组res,所以空间复杂度也是O(n)。
参考
https://leetcode-cn.com/problems/cong-wei-dao-tou-da-yin-lian-biao-lcof/
https://time.geekbang.org/column/article/41013
本文转载自微信公众号「码上积木」,可以通过以下二维码关注。转载本文请联系码上积木公众号。