随着深度学习的蓬勃发展,越来越多的小伙伴开始尝试搭建深层神经网络应用于工作场景中,认为只需要把数据放入模型中,调优模型参数就可以让模型利用自身机制来选择重要特征,输出较好的数据结果。
在现实工作场景中,受限制数据和时间,这样的做法其实并不可取,一方面大量数据输入将导致模型训练周期增长,另一方面在当前细分市场中,并非所有场景都有海量数据,寻找海量数据中的重要特征迫在眉睫。
本文我将教你三个选择特征的方法,这是任何想从事数据科学领域的都应该知道。本文的结构如下:
- 数据集加载和准备
- 方法1:从系数获取特征重要性
- 方法2:从树模型获取特征重要性
- 方法3:从 PCA 分数中获取特征重要性
- 结论
数据集加载和准备
为了方便介绍,我这里使用"load_breast_cancer"数据集,该数据内置于 Scikit-Learn 中。
以下代码段演示如何导入库和加载数据集:
- import numpy as np
- import pandas as pd
- from sklearn.datasets import load_breast_cancer
- import matplotlib.pyplot as plt
- from matplotlib import rcParams
- rcParams['figure.figsize'] = 14, 7
- rcParams['axes.spines.top'] = False
- rcParams['axes.spines.right'] = False
- # Load data
- data = load_breast_cancer()
调用以下代码,输出结果。
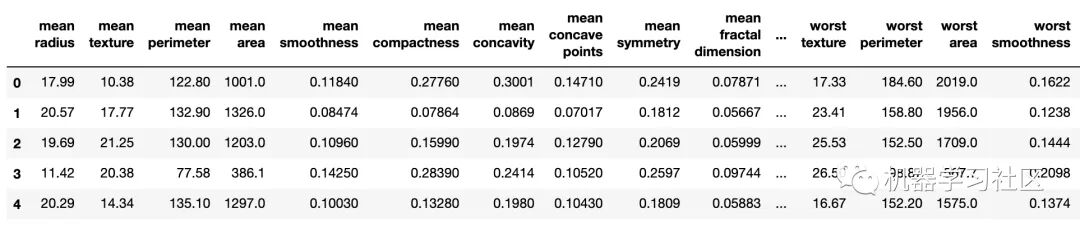
- df = pd.concat([pd.DataFrame(data.data, columns=data.feature_names),pd.DataFrame(data.target, columns=['y'])], axis=1)
- df.head()
上述数据中有 30 个特征变量和一个目标变量。所有值都是数值,并且没有缺失的值。在解决缩放问题之前,还需要执行训练、测试拆分。
- from sklearn.preprocessing import StandardScaler
- from sklearn.model_selection import train_test_split
- X = df.drop('y', axis=1)
- y = df['y']
- X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=42)
- ss = StandardScaler()
- X_train_scaled = ss.fit_transform(X_train)
- X_test_scaled = ss.transform(X_test)
方法1:从系数获取特征重要性
检查特征重要性的最简单方法是检查模型的系数。例如,线性回归和逻辑回归都归结为一个方程,其中将系数(重要性)分配给每个输入值。
简单地说,如果分配的系数是一个大(负或正)数字,它会对预测产生一些影响。相反,如果系数为零,则对预测没有任何影响。
逻辑非常简单,让我们来测试一下,逻辑回归是一种合适的算法。拟合模型后,系数将存储在属性中coef_。
- from sklearn.linear_model import LogisticRegression
- model = LogisticRegression()
- model.fit(X_train_scaled, y_train)
- importances = pd.DataFrame(data={
- 'Attribute': X_train.columns,
- 'Importance': model.coef_[0]
- })
- importances = importances.sort_values(by='Importance', ascending=False)
- # 可视化
- plt.bar(x=importances['Attribute'], height=importances['Importance'], color='#087E8B')
- plt.title('Feature importances obtained from coefficients', size=20)
- plt.xticks(rotation='vertical')
- plt.show()
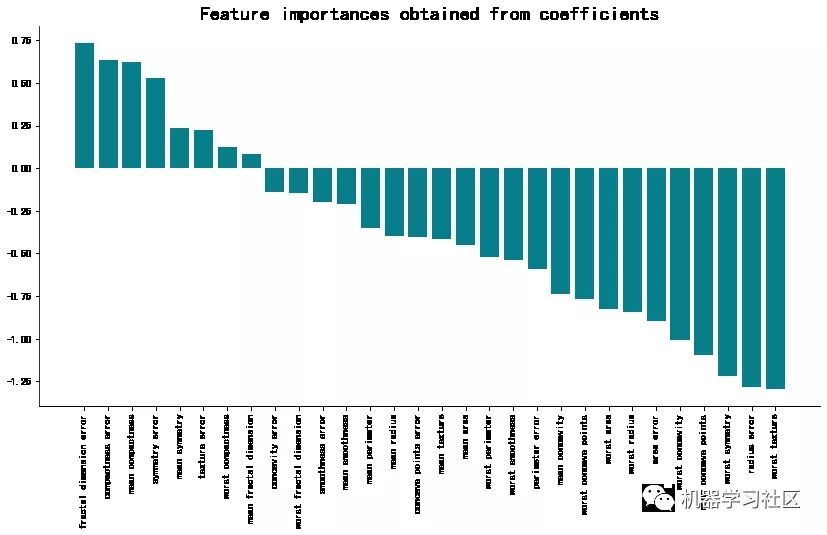
下面是相应的可视化效果:
该方法最大特点:「简单」、「高效」。系数越大(在正方向和负方向),越影响预测效果。
方法2:从树模型获取重要性
训练任何树模型后,你都可以访问 feature_importances 属性。这是获取功特征重要性的最快方法之一。
以下代码演示如何导入模型并在训练数据上拟合模型,以及重要性的获取:
- from xgboost import XGBClassifier
- model = XGBClassifier()
- model.fit(X_train_scaled, y_train)
- importances = pd.DataFrame(data={
- 'Attribute': X_train.columns,
- 'Importance': model.feature_importances_
- })
- importances = importances.sort_values(by='Importance', ascending=False)
- # 可视化
- plt.bar(x=importances['Attribute'], height=importances['Importance'], color='#087E8B')
- plt.title('Feature importances obtained from coefficients', size=20)
- plt.xticks(rotation='vertical')
- plt.show()
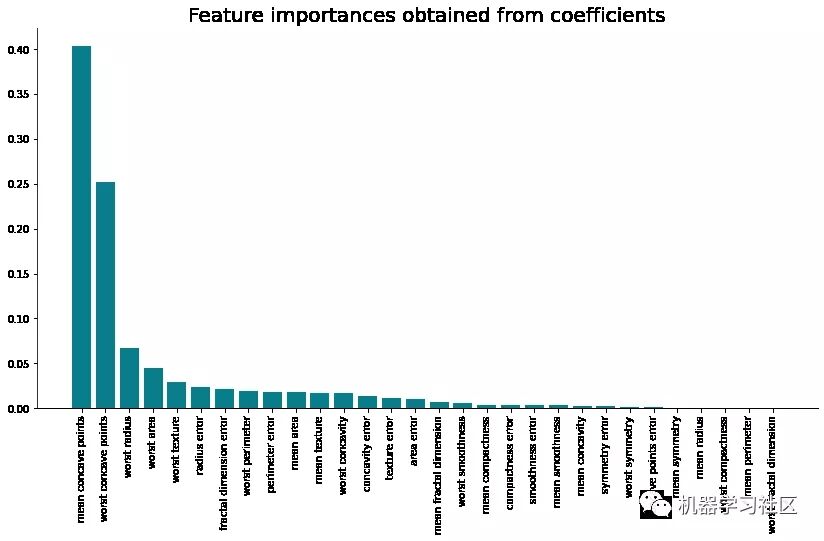
相应的可视化效果如下所示:
方法3:从 PCA 分数获取特征重要性
主成分分析(PCA)是一种出色的降维技术,也可用于确定特征的重要性。
PCA 不会像前两种技术那样直接显示最重要的功能。相反,它将返回 N 个主组件,其中 N 等于原始特征的数量。
- from sklearn.decomposition import PCA
- pca = PCA().fit(X_train_scaled)
- # 可视化
- plt.plot(pca.explained_variance_ratio_.cumsum(), lw=3, color='#087E8B')
- plt.title('Cumulative explained variance by number of principal components', size=20)
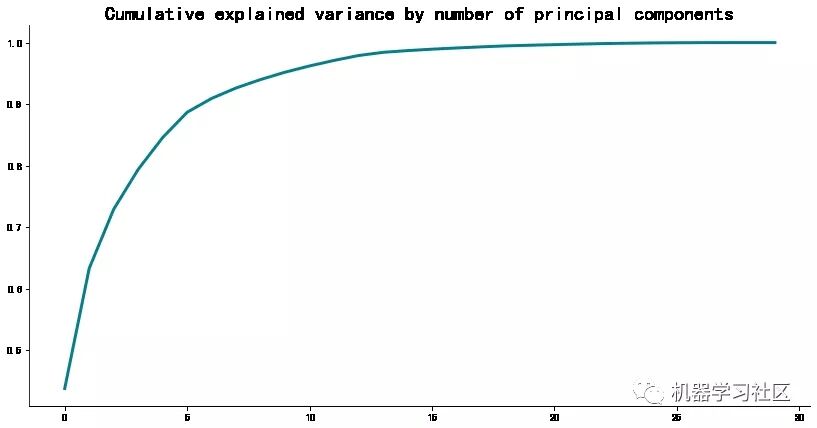
- plt.show()
但这是什么意思呢?这意味着你可以使用前五个主要组件解释源数据集中 90%的方差。同样,如果你不知道这意味着什么,继续往下看。
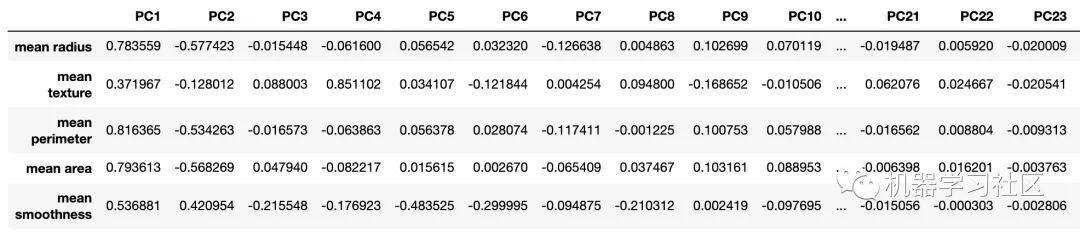
- loadings = pd.DataFrame(
- data=pca.components_.T * np.sqrt(pca.explained_variance_),
- columns=[f'PC{i}' for i in range(1, len(X_train.columns) + 1)],
- index=X_train.columns
- )
- loadings.head()
第一个主要组成部分至关重要。它只是一个要素,但它解释了数据集中超过 60% 的方差。从上图中可以看到,它与平均半径特征之间的相关系数接近 0.8,这被认为是强正相关。
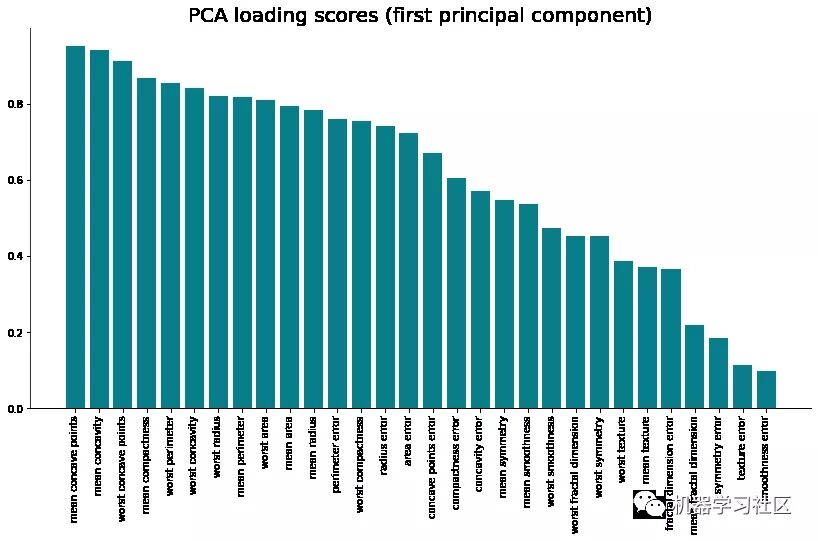
让我们可视化所有输入要素与第一个主组件之间的相关性。下面是整个代码段(包括可视化):
- pc1_loadings = loadings.sort_values(by='PC1', ascending=False)[['PC1']]
- pc1_loadings = pc1_loadings.reset_index()
- pc1_loadings.columns = ['Attribute', 'CorrelationWithPC1']
- plt.bar(x=pc1_loadings['Attribute'], height=pc1_loadings['CorrelationWithPC1'], color='#087E8B')
- plt.title('PCA loading scores (first principal component)', size=20)
- plt.xticks(rotation='vertical')
- plt.show()
这就是如何"破解"PCA,使用它作为特征重要性的方法。
结论
上述总结来 3 个机器学习特征重要性的方法,这三个可根据场景灵活运用。如果你对机器学习感兴趣,可以关注我。