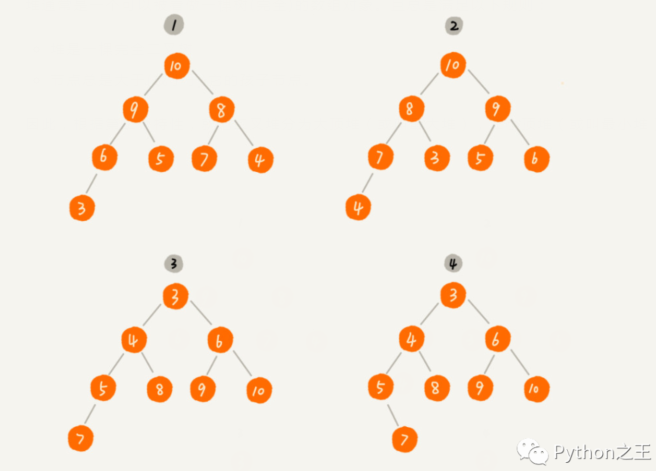
堆通常是一个可以被看做一棵树(完全)的数组对象。且总是满足以下规则：
堆是一棵完全二叉树
节点总是大于(或小于)它的孩子节点。
因此，根据第二个特性，就把二叉堆分为大顶堆(或叫最大堆)，和小顶堆(或叫最小堆)。
在上图中，1 2 是大顶堆 ，3 4 是小顶堆。判断是不是堆的条件：「从根结点到任意结点路径上结点序列的有序性!大顶堆和小顶堆判断序列是顺序还是逆序!」
Python并没有提供“堆”这种数据类型，它是直接把列表当成堆处理的。Python提供的heapq包中有一些函数，提供执行堆操作的工具函数
- >>> import heapq
- >>> heapq.__all__
- ['heappush', 'heappop', 'heapify', 'heapreplace', 'merge', 'nlargest', 'nsmallest', 'heappushpop']
堆排序
往堆中插入一个元素后，我们就需要进行调整，让其重新满足堆的特性，这个过程叫做堆化(heapify)。
那么堆排序的基本思路是怎么样的呢?
- 将待排序序列构建成一个堆 H[0……n-1]，根据(升序降序需求)选择大顶堆或小顶堆;
- 把堆首(最大值)和堆尾互换;
- 顺着节点所在的路径，向上或者向下，对比，然后交换，目的是把新的数组顶端数据调整到相应位置;
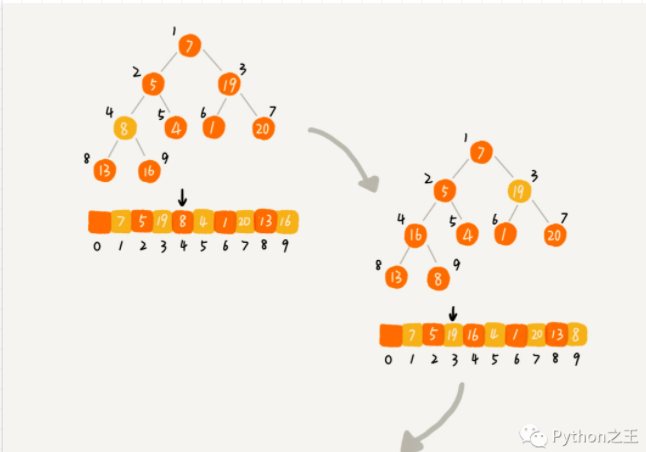
下面举个例子(资源来自王争算法)，比如在上面的大顶堆中添加数据22。
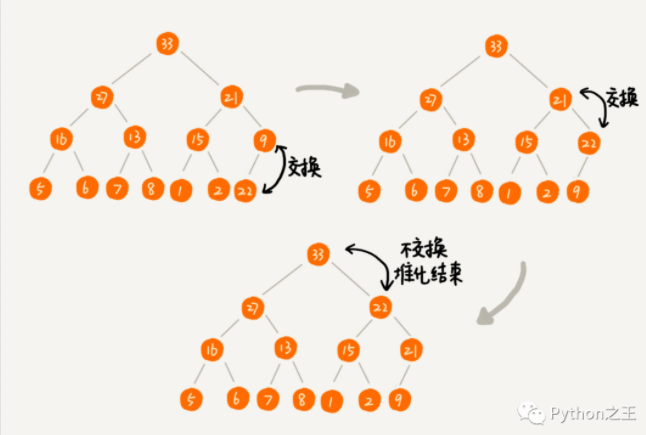
堆化非常简单，就是顺着节点所在的路径，向上或者向下，对比，然后交换。
堆排序的删除操作，这里一般指的是堆顶元素，当我们删除堆顶元素之后，就需要把第二大的元素放到堆顶，那第二大元素肯定会出现在左右子节点中。
然后我们再迭代地删除第二大节点，以此类推，直到叶子节点被删除。但是这样会产生一个数组空洞的问题。
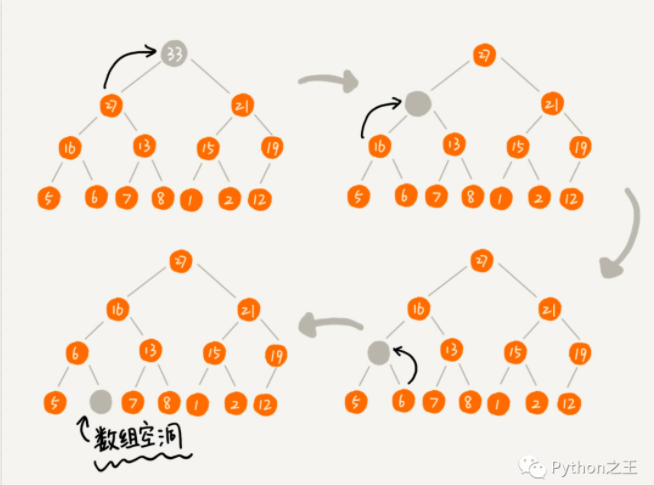
因此，这里面又个技巧，就是删除堆顶元素的时候，不能直接删除，要用堆顶元素和最后一个元素做交换，然后根据堆的特点调整堆，直到满足条件。
排序的过程就是每次待排序的序列长度减去1再执行这两步。
下面给出通过Python中的heapq模块实现的堆排序简单代码。
- from heapq import heappop, heappush
- def heap_sort(array):
- heap = []
- for element in array:
- heappush(heap, element)
- ordered = []
- while heap:
- ordered.append(heappop(heap))
- return ordered
- array = [13, 21, 15, 5, 26, 4, 17, 18, 24, 2]
- print(heap_sort(array))
- # [2, 4, 5, 13, 15, 17, 18, 21, 24, 26]
如果不使用heapq模块，对于推排序需要了解堆排序中的建堆过程。
将数组原地建成一个堆。不借助另一个数组，就在原数组上操作。建堆的过程，有两种思路。
第一种建堆思路的处理过程是从前往后处理数组数据，并且每个数据插入堆中时，都是从下往上堆化。而第二种实现思路，是从后往前处理数组，并且每个数据都是从上往下堆化。
- 补充：利用层序遍历(遍历方式还有前中后)映射到数组后，假设树或子树的根节点为arr[root],则其对应的子节点分别为arr[root*2+1],arr[root*2+2]。
也就是如果节点的下标是 i，那左子节点的下标就是 2∗i+1，右子节点的下标就是 2∗i+2，父节点的下标就是 。
- def heap_sort(array):
- n = len(array)
- # 从尾部开始建堆，这样保证子节点有序
- for i in range((n-1)//2, -1, -1):
- _shift(array, n, i)
- # 依次把堆顶元素交换到最后，重建堆顶（堆不包含刚交换的最大元素）
- for i in range(n-1, 0, -1):
- array[0], array[i] = array[i], array[0]
- _shift(array, i, 0)
- return array
- # 重建堆顶元素 n：堆元素个数，i：堆建顶位置
- def _shift(array, n, i):
- # 如果没有子节点，直接返回
- if i*2+1 >= n:
- return
- # 取最大子节点位置
- maxsub = i*2+2 if i*2+2 < n and array[i*2+1] <= array[i*2+2] else i*2+1
- # 如果节点小于最大子节点，交换元素，递归以子节点为堆顶重建
- if array[i] < array[maxsub]:
- array[i], array[maxsub] = array[maxsub], array[i]
- _shift(array, n, maxsub)
- if __name__ == '__main__':
- array = [13, 21, 15, 5, 26, 4, 17, 18, 24, 2]
- print(heap_sort(array))
- # [2, 4, 5, 13, 15, 17, 18, 21, 24, 26]
堆排序不是稳定的排序算法，因为在排序的过程，存在将堆的最后一个节点跟堆顶节点互换的操作，所以就有可能改变值相同数据的原始相对顺序。堆排序整体的时间复杂度是O(nlogn) 。
参考资料 https://github.com/MaoliRUNsen/runsenlearnpy100
