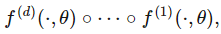> Image by Alina Grubnyak on Unsplash
神经网络是将数据映射到信息的通用逼近器。这是什么意思?神经网络可以解决任何问题吗?神经网络是一种经过验证的解决方案,可用于按场景/逐帧分析,股票价格预测,零售,以及许多其他目的。我们中的许多人在企业级别使用它,但是我们当中有多少人真正理解它呢?
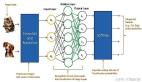
要回答"神经网络可以解决任何问题吗?"的问题,让我们从基础上进行探讨。NeuralNet由称为层的垂直堆叠组件组成:输入,隐藏和输出。每层由一定数量的神经元组成。输入层具有数据集的属性(特征)。根据问题陈述,可以存在具有多个神经元的多个隐藏层,而输出层可以具有多个神经元。
了解感知器和激活功能
感知器(或神经元)是神经网络的基本粒子。它根据阈值化原理工作。令f(x)是一个阈值为40的求和函数。
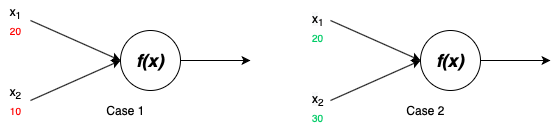
> Fig 1. Firing of Neurone (Image by Author)
在两种情况下,定义的函数都返回两个输入x 1和x 2的加法。在情况1中,函数返回小于阈值的30。在情况2中,该函数返回大于阈值的50,并且神经元将触发。现在,此功能变得比这复杂。典型神经网络的神经元接收输入值的总和乘以其权重和增加的偏差,该函数(也称为激活函数或步进函数)有助于做出决策。
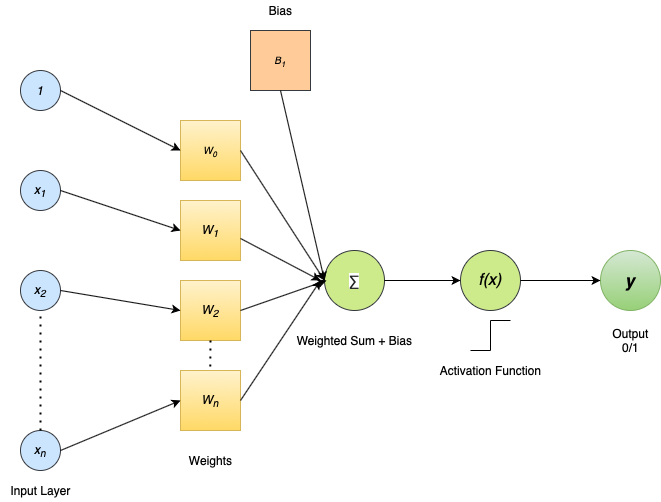
> Fig 2. Perceptron (Image by Author)
激活函数将节点的输出转换为二进制输出。如果加权输入超过阈值,则为1,否则为0(取决于激活功能)。共有三种最常用的激活功能:
Sigmoid
Sigmoid是一种广泛使用的激活函数,有助于捕获非线性关系。
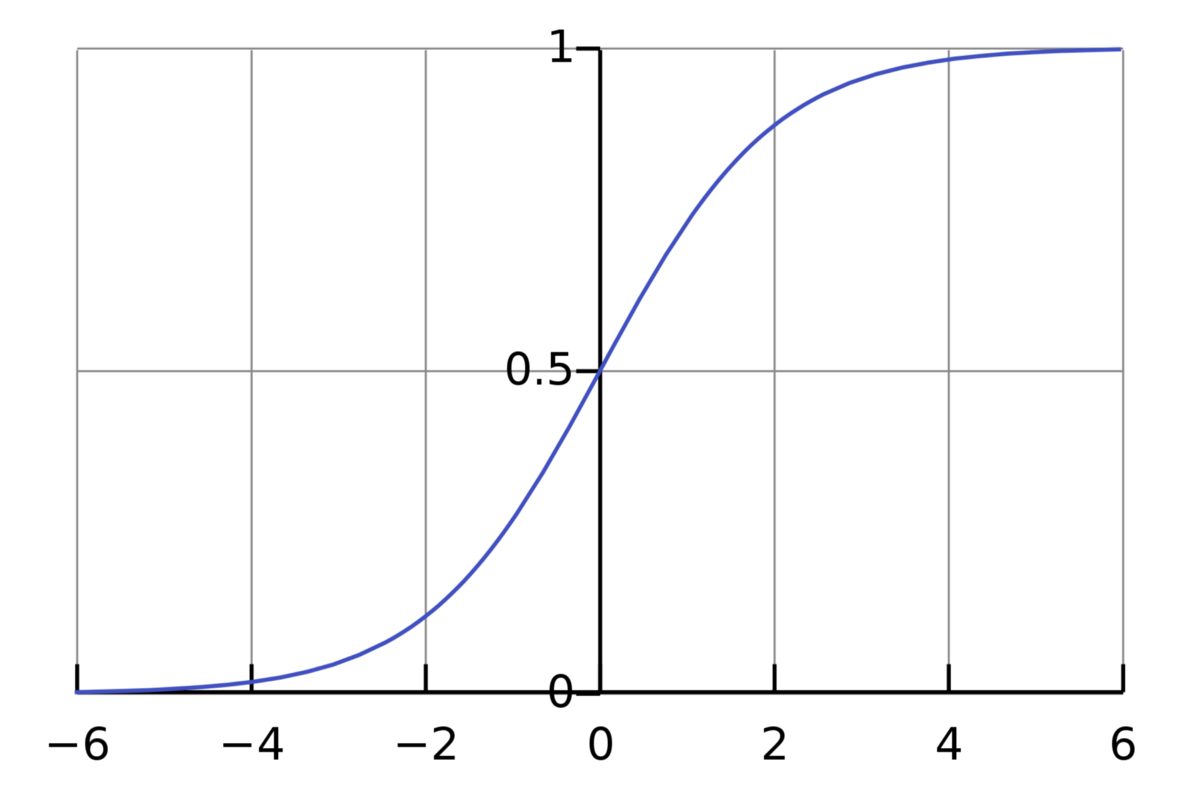
> Fig 3. Sigmoid Curve (source)
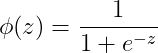
对于任何z值,函数Φ(z)将始终返回二进制(0/1)输出。因此,它被广泛用于基于概率的问题中。
tanh(Tangent双曲线)
它或多或少像Sigmoid函数,但tanh的范围是-1到1,这使其适合分类问题。它是非线性的。
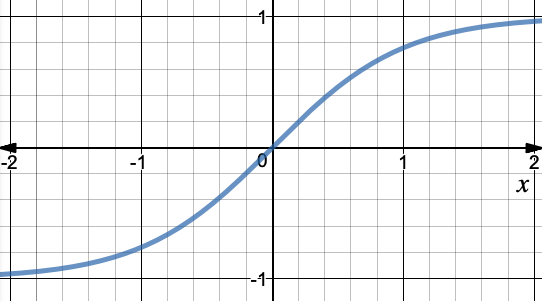
> Fig 4. tanh curve (Image by Author)
ReLu(整流线性单位)
它是深度学习中最常用的激活函数,因为它不像其他激活函数那样复杂。f(x)返回0或x。
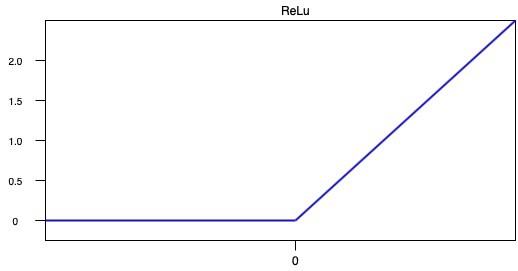
> Fig 5. ReLu curve (Image by Author)
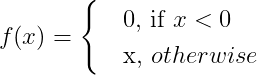
由于ReLu函数的导数返回0或1,这使计算变得容易。
神经网络
为了理解神经网络的黑匣子,让我们考虑一个具有三层的基本结构。输入层,密集/隐藏层(连接在神经元的两侧)和输出层。
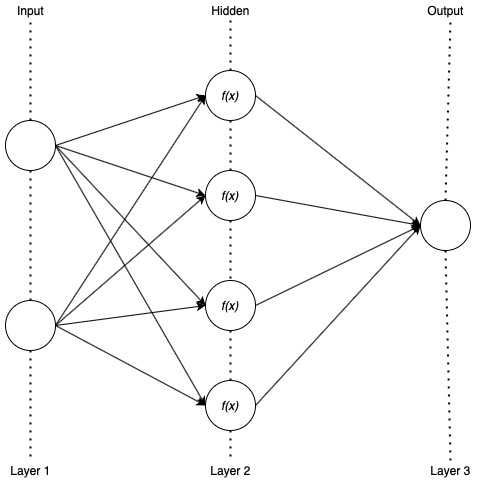
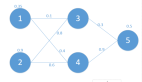
> Fig 6. A simple Neural Network (Image by Author)
权重和偏差是随机初始化的。神经网络输出的准确性在于通过不断更新权重和偏差来找到最佳值。让我们考虑一个方程,y = wx其中" w"是权重参数," x"是输入特征。简而言之,权重定义了赋予特定输入属性(功能)的权重。现在,方程y = wx的解将始终通过原点。因此,增加了一个截距以提供自由度,以适应被称为偏差的完美拟合,并且方程式变为我们都熟悉的ŷ= wx + b。因此,偏置可以使激活函数的曲线向上或向下调整轴。
现在让我们看看神经网络会变得多么复杂。对于我们的网络,输入层有两个神经元,密集层有四个神经元,输出层有一个。每个输入值都与其权重和偏差相关联。输入特征与权重和偏差的组合通过密集层,在该层中,网络借助激活函数学习特征,并且网络具有自己的权重和偏差,最后进行预测(输出)。这就是正向传播。那么,我们的网络有多少个总参数?
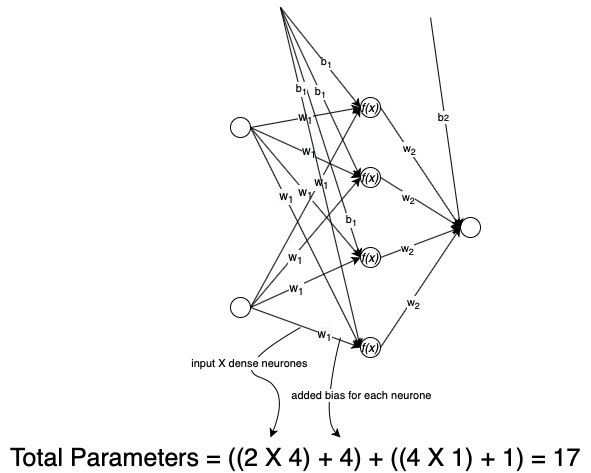
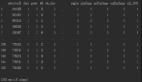
> Fig 7. Total Parameter calculation of a Neural Network (Image by Author)
对于这样一个简单的网络,总共需要优化17个参数才能获得最佳解决方案。随着隐藏层数量和其中神经元数量的增加,网络获得了更大的功率(达到特定点),但是随后我们需要指数级的参数进行优化,这可能最终会占用大量的计算资源。因此,需要进行权衡。
更新网络
在一次正向传播迭代之后,通过获取实际输出与预测输出之间的(平方)差来计算误差。在网络中,输入和激活功能是固定的。因此,我们可以更改权重和偏差以最小化误差。可以通过注意两点来最大程度地减少错误:通过少量更改权重来更改错误,以及更改的方向。
成本函数
一个简单的神经网络根据线性关系value = wx + b来预测值,其中ŷ(预测)是y(实际)的近似值。现在,可以有几条拟合linear的直线。为了选择最佳拟合线,我们定义了成本函数。
令ŷ=θ₀+xθ₁。我们需要找到θ₀和θ₁的值,以使ŷ与y尽可能接近。为此,我们需要找到θ₀和θ₁的值,以使以下定义的误差最小。
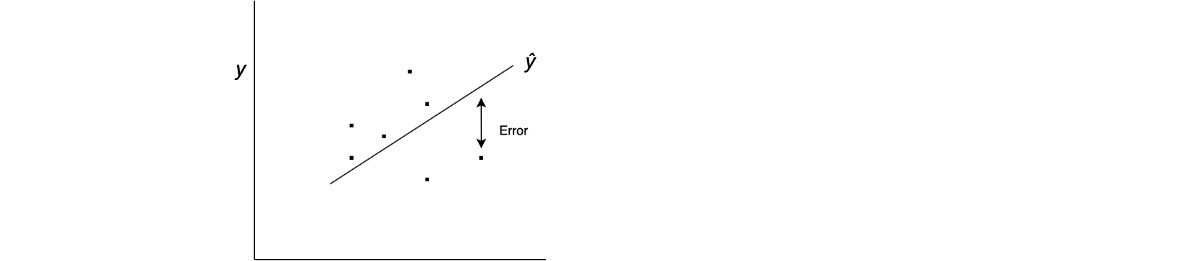
> (Image by Author)
误差,E =实际值和预测值之间的平方差=(=-y)²
因此,Cost =(1 / 2n)(θ₀+xθ₁-y)²,其中n是用于计算均方差的总点数,并且将其除以2以减少数学计算量。因此,我们需要最小化此成本函数。
梯度下降
通过最小化成本函数,该算法有助于找到θ₀和θ₁的最佳值。我知道C =(1 / 2n)(θ₀+xθ₁— y)²。对于分析解决方案,我们将C相对于变量(θ)(称为梯度)进行了部分微分。
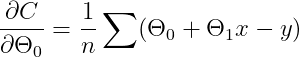

这些梯度表示斜率。现在,原始成本函数是二次函数。因此,该图将如下所示:
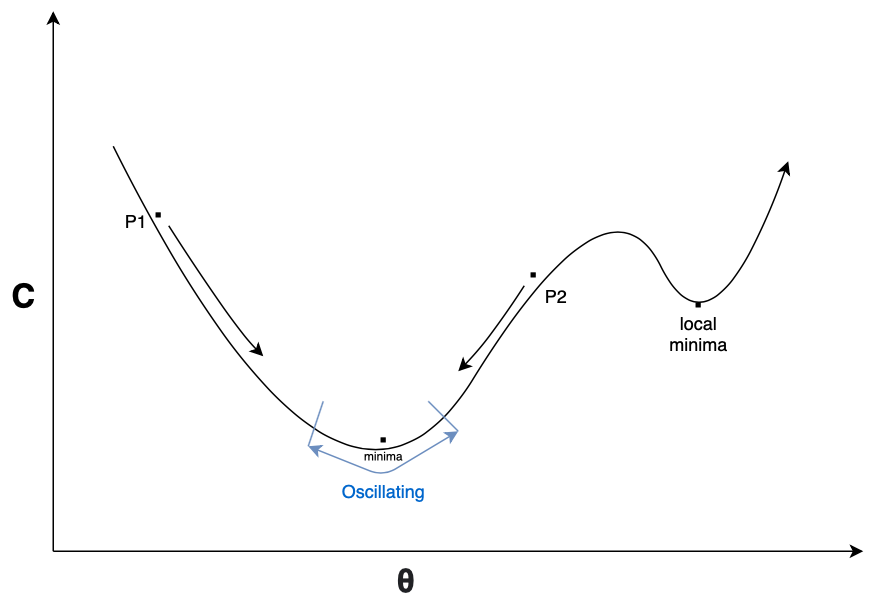
> Fig 8. Gradient Descent curve (Image by Author)
更新θ的公式为:
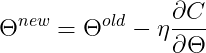
如果我们在点P1处,则斜率为负,这使梯度为负,整个方程为正。因此,该点沿正方向向下移动,直到达到最小值。类似地,如果我们在点P2处,则坡度为正,这使梯度为正,整个方程为负,使P2沿负方向移动,直到达到最小值。此处,η是点趋于极小值的速率,称为学习速率。所有θ都会同时更新(对于某些时期),并计算误差。
附带说明
通过这样做,我们可能会遇到两个潜在问题:1.在更新θ值时,您可能会陷入局部最小值。一种可能的解决方案是使用具有动量的随机梯度下降(SGD),这有助于越过局部极小值。2.如果η太小,收敛将花费很长时间。或者,如果η太大(或什至中等偏高),它将继续围绕最小值振荡,并且永远不会收敛。因此,我们不能对所有参数使用相同的学习率。为了解决这个问题,我们可以安排一个例程,该例程会随着梯度向最小值移动(例如余弦衰减)而调整η的值。
后向传播
使用梯度下降算法优化和更新NeuralNet中的权重和偏差的一系列操作。让我们考虑一个具有输入,单个隐藏层和输出的简单神经网络(图2)。
设x为输入,h为隐藏层,σ为S型激活,w权重,b为偏置,wᵢ为输入权重,wₒ为输出权重,bᵢ为输入偏置,bₒ为输出偏置,O为输出,E为误差和μ是线性变换((∑wᵢxᵢ)+ b)。
现在,我们通过堆叠从输入到输出所需的一系列操作来创建图2的计算图。

> Fig 9. Computation Graph (Image by Author)
这里,E依赖于O,O依赖于μ2,μ2依赖于b 1,w 3和h,h依赖于μ1,并且μ1依赖于x,w 1和b 5。我们需要计算权重和偏差的中间变化(相关性)。由于只有一层隐藏层,因此存在输入和输出权重和偏差。因此,我们可以将其分为两种情况。
案例1:w.r.t.输出权重和偏差
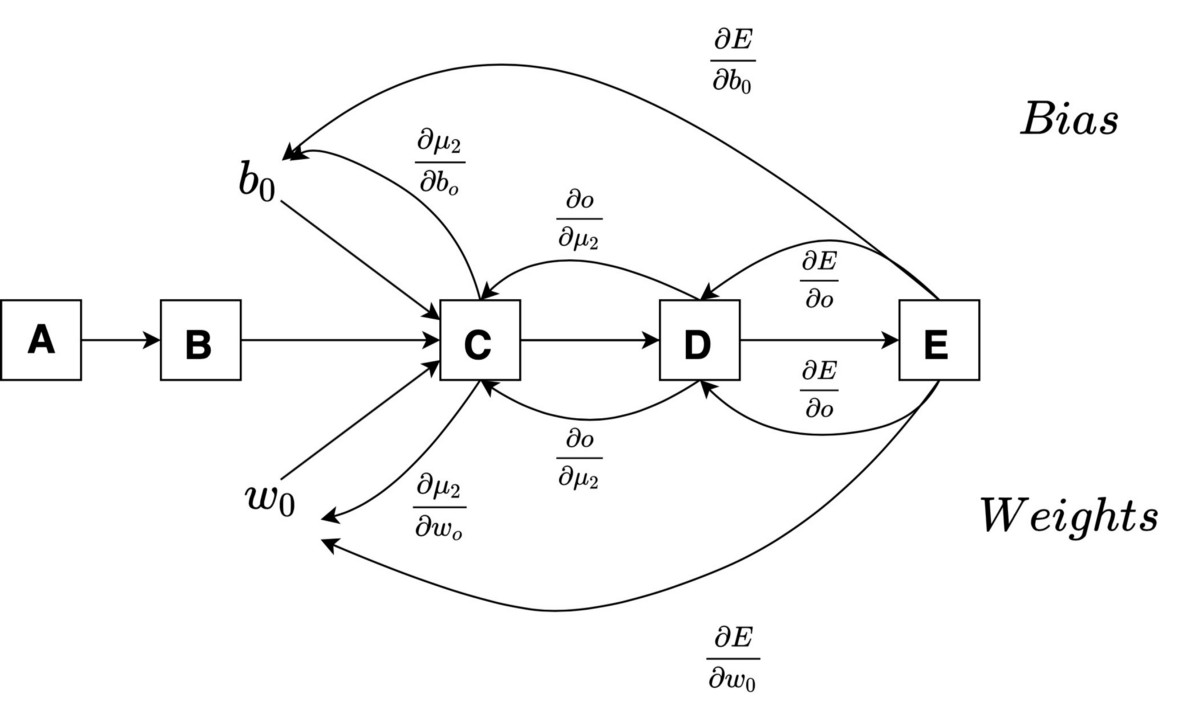
> Fig 10. Computation Graph for case 1 (Image by Author)

因此,通过将导数的值放在上述两个误差变化方程中,可以得到如下的梯度
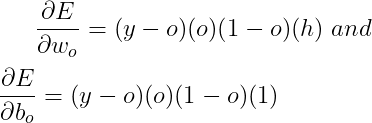
我们可以通过以下公式更新权重和偏差:
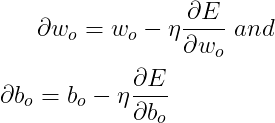
此计算用于隐藏层和输出。同样,对于输入和隐藏层如下。
情况2:w.r.t。输入权重和偏差
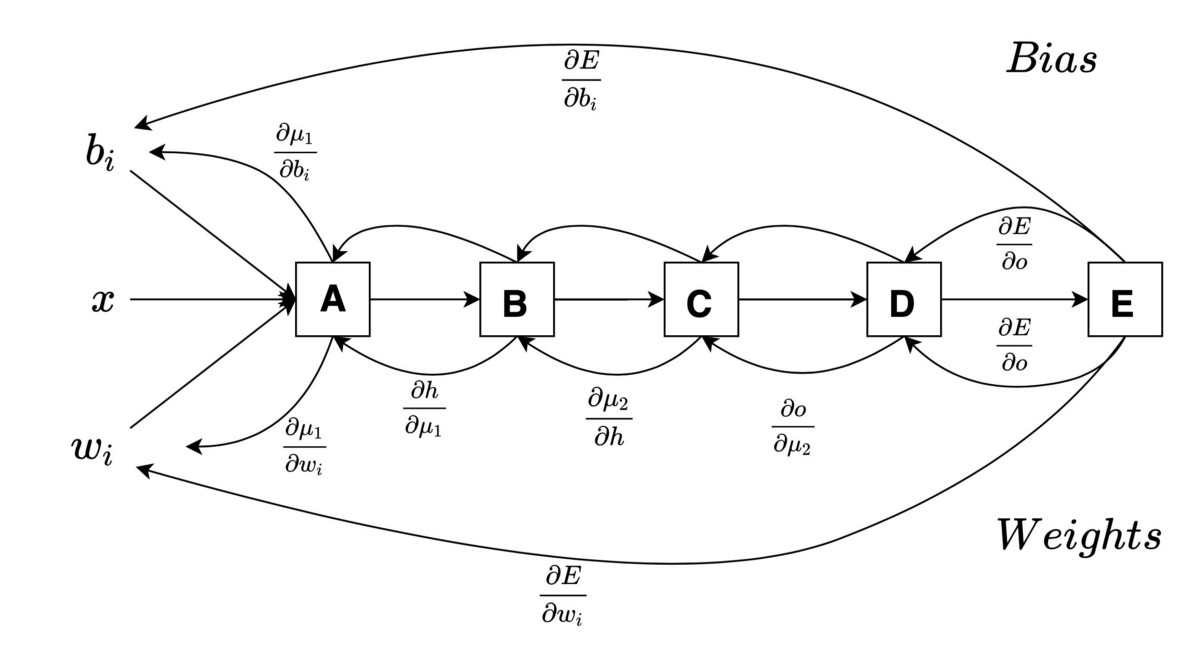
> Fig 11. Computation Graph for case 2. (Image by Author)
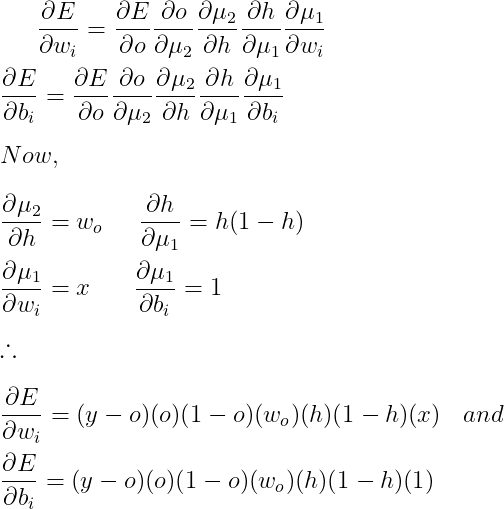
我们可以使用以下方法更新这些渐变:
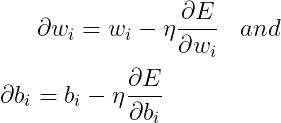
两种情况同时发生,并且计算错误直到重复的次数称为时期。对神经网络进行监督。在运行了一定数量的时间后,我们为数据集的选定要素设置了一组优化的权重和偏差。当在此优化网络中引入新输入时,将使用权重和偏差的优化值来计算它们,以实现最大精度。
神经网络可以解决任何问题吗?
如上所述,神经网络是通用逼近器。从理论上讲,它们能够代表任何功能,因此可以解决任何问题。随着网络的增长(更多的隐藏层),它会获得更多的功能,但是要优化的参数数量呈指数级增长,这会占用大量资源。
可以在这里找到实现。
本文由闻数起舞翻译自Shubham Dhingra的文章《Simplified Mathematics behind Neural Networks》,转载请注明出处,原文链接:https://towardsdatascience.com/simplified-mathematics-behind-neural-networks-f2b7298f86a4)