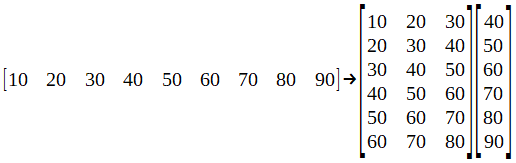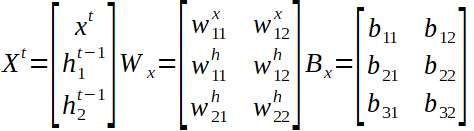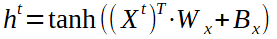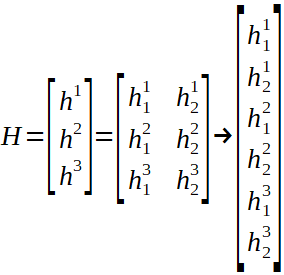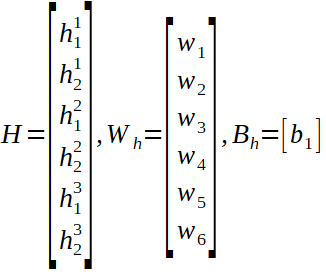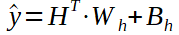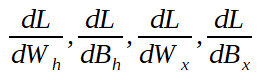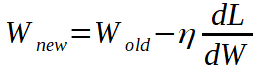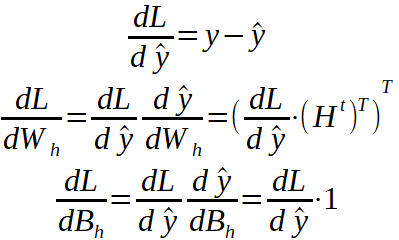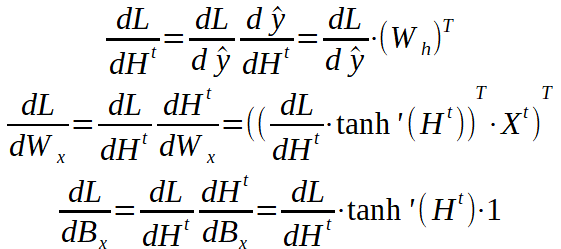让我向您展示什么是RNN,在哪里使用,它们如何向前和向后传播以及如何在PyTorch中使用它们。
大多数类型的神经网络都可以对要对其进行训练的样本进行预测。一个主要的例子是MNIST数据集。像MLP这样的常规神经网络知道有10位数字,即使图像与训练网络上的图像非常不同,它也仅基于它们进行预测。
现在,假设我们可以通过提供9个有序数字的序列,并让网络猜测第10个数字,来利用这种网络进行顺序分析。网络不仅会知道如何区分10位数字,而且还会知道从0到8的顺序,下一位数字很可能是9。
在分析序列数据时,我们了解到,序列中的元素通常以某种方式相关,这意味着它们彼此依赖。因此,我们需要考虑每个元素以了解序列的想法。
剑桥大学出版社将序列定义为"事物或事件彼此跟随的顺序",或者最重要的是,"一系列相关事物或事件"。为了将此定义调整到深度学习的范围内,顺序是一组包含可训练上下文的数据,删除一些元素可能会使它无用。
但是序列包含什么?哪些分组数据可以具有上下文?以及如何提取上下文来利用神经网络的力量?在进入神经网络本身之前,让我向您展示使用递归神经网络(RNN)经常解决的两种类型的问题。
时间序列预测
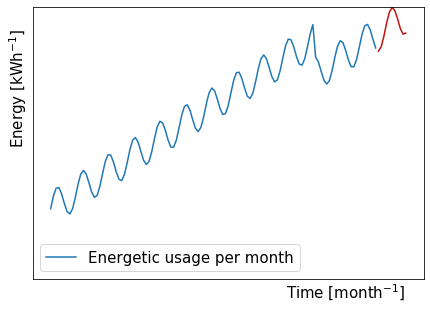
第一个示例是时间序列预测问题,其中我们用一系列现有数值(蓝色)训练神经网络,以便预测未来的时间步长(红色)。
如果我们按照这些家庭多年来的每月精力支出进行排序,我们可以看到正弦曲线趋势呈上升趋势,而突然下降。
正弦曲线部分的背景可能是整个夏季(从夏季到冬季)再到夏季的不同能量需求。精力充沛的支出增长可能来自使用更多的电器和设备,或者转换为可能需要更多能源的更强大的电器和设备。突然跌倒的背景可能意味着一个人长大了足以离开家,而那个人所需的能量不再在那里。
您越了解上下文,通常可以通过连接输入向量将更多信息提供给网络,以帮助网络理解数据。在这种情况下,对于每个月,我们可以将三个更多的值与能源联系起来,这些价值包括电器和设备的数量,其能量效率以及家庭容纳的人数。
自然语言处理
玛丽骑自行车,自行车是____。
第二个例子是自然语言处理问题。这也是一个很好的例子,因为神经网络必须考虑现有句子提供的上下文来完成它。
假设我们的网络经过训练,可以用所有格代词完成句子。一个受过良好训练的网络将理解该句子是用第三人称单数构成的,并且Mary最有可能是女性名字。因此,预测代词应该是"她的"而不是男性的"他的"或复数的"他们的"。
现在,我们已经看到了两个排序数据的例子,让我们探索网络向前和向后传播的过程。
RNN配置
如我们所见,RNN从序列中提取信息以提高其预测能力。
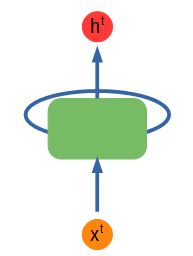
> Simple recurrent network diagram. Figure by author.
上面显示了一个简单的RNN图。绿色节点输入一些输入x ^ t并输出一些值h ^ t,该值也被馈送到该节点,再次包含从输入中收集的信息。不管馈入节点的内容有什么模式,它都会学习并保留该信息以供下一次输入。上标t代表时间步长。
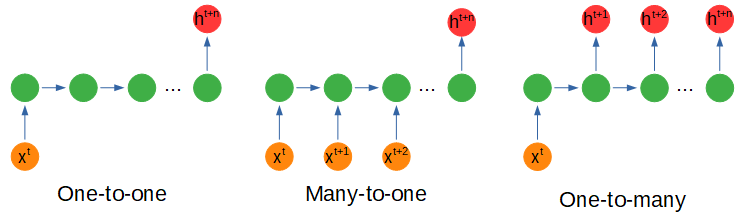
> Recurrent network configurations. Figure by author.
根据输入或输出的形状,神经网络的配置会有一些变化,稍后我们将了解节点内部会发生什么。
多对一配置是指我们以不同的时间步长输入多个输入以获得一个输出时,这可能是在电影场景的各个帧中捕获的情感分析。
一对多使用一个输入来获取多个输出。例如,我们可以使用多对一配置对表达某种情感的诗歌进行编码,并使用一对多配置来创建具有相同情感的新诗行。
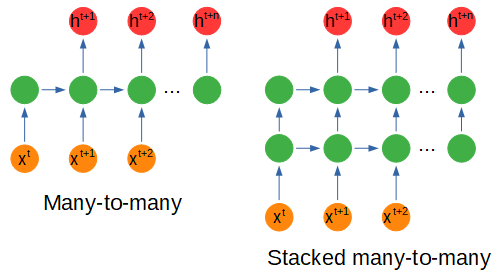
多对多使用多个输入来获取多个输出,例如使用一系列值(例如在能量使用中)并预测未来的十二个月而不是一个月。
堆叠配置只是一个具有多个隐藏节点层的网络。
RNN前传
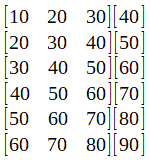
为了了解神经网络节点内部发生的情况,我们将使用一个简单的数据集作为"时间序列预测"示例。贝娄是价值的完整序列,它是作为培训和测试数据集而进行的重组。
我从这个网站上拿了这个例子,这是一般而言深度学习的重要资源。现在,让我们将数据集分成批次。
我在这里没有显示它,但不要忘记应该对数据集进行规范化。这很重要,因为神经网络对数据集值的大小很敏感。
这个想法是预测未来的价值。因此,假设我们选择了该批次的第一行:[10 20 30],在训练了我们的网络之后,我们应该得到40的值。要测试神经网络,可以将向量输入[70 80 90],并期望获得一个如果网络训练有素,则值接近100。
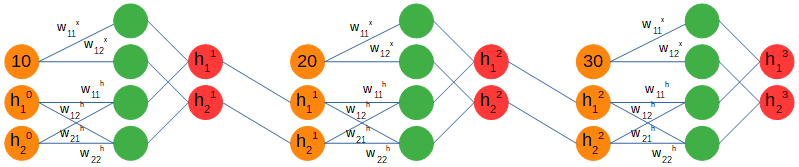
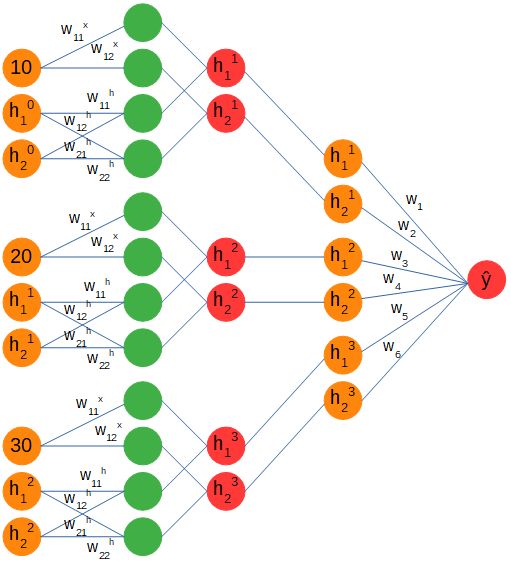
我们将使用多对一配置,分别提供每个序列的三个时间步。当使用递归网络时,输入值不是进入网络的唯一值,还有一个隐藏的数组,该数组的结构将在节点之间传递序列的上下文。我们将其初始化为零数组,并将其连接到输入。它的尺寸(1 x 2)是个人选择,只是使用与1 x 1步进输入不同的尺寸。
> Recurrent forward pass. Figure by author.
仔细观察,我们可以看到权重矩阵分为两部分。第一个处理输入创建两个输出,第二个处理隐藏数组创建两个输出。然后将这两组输出加在一起,并获得一个新的隐藏数组,其中包含来自第一个输入(10)的信息,并将其馈送到下一个时间步输入(20)。应当注意,权重和偏差矩阵在时间步长之间是相同的。
上面表示了全局输入向量X ^ t,权重矩阵W和偏置矩阵B以及隐藏数组的计算。仅剩一个步骤才能完成前进。我们正在尝试预测一个未来的价值,我们有三个隐藏的数组,每个输入的信息作为输出,因此我们需要将它们转换为单个值,希望在经过许多次培训后才是正确的值。
通过连接并重塑数组,我们可以附加一个线性层来计算最终结果。完整的网络具有以下形式:
> Full recurrent diagram. Figure by author.
您可以看到多对一配置吗?我们从一个序列中馈入三个输入,它们的上下文由权重和偏差矩阵捕获,并存储在一个隐藏的数组中,该数组在每个时间步都用新信息更新。最终,存储在隐藏数组中的上下文将经历另一组权重和偏差,并且在将序列的所有时间步长输入到网络之后,将输出一个值。
我们可以看到隐藏状态的线性形式以及线性层的权重和偏差矩阵,以及预测值的计算(y hat)。
现在,这是RNN的前向传播,但我们仍然没有看到向后传递。
RNN向后传递
向后传播是训练每个神经网络的非常重要的一步。在此,预测输出和实际值之间的误差朝着神经网络传播,目的是改善权重和偏差,以便每次迭代都能获得更好的预测。
在大多数情况下,此步骤由于其复杂性而被忽略了。在提及重要内容的同时,我将向您提供一个尽可能简单的解释。
向后传递是使用微积分的链法则从损耗到所有权重和偏差参数的一系列推导。这意味着我们最终需要以下值(如果是多维的,则为数组):
如果您不熟悉一阶导数的数学含义,但实际上,当一阶导数为零时,我通常建议您阅读有关梯度下降的文章,这通常意味着我们在系统中找到了一个最小值,并且理想情况下我们将无法进一步改善它。
这里需要注意的一点是:零也可能是最大值,它是不稳定的,不应在那里进行优化,或者是鞍点,其本身也不是很稳定。最小值可以是全局值(函数的最小值)或局部值。这对我的解释并不重要,但是如果您想了解更多信息,可以查找一下!
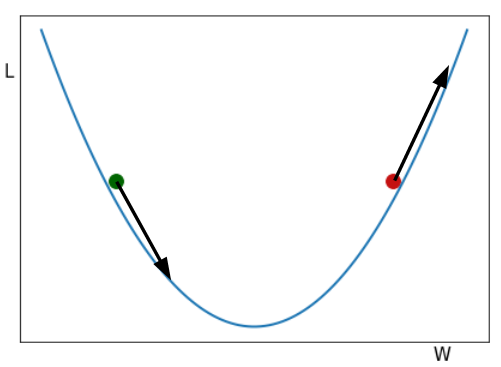
> Gradient Descent example. Two balls rolling down the hill. Figure by author.
您在图片中看到的是两个球从山谷中滚下来。从视觉上看,一阶导数给了我们山坡的大小。如果我们沿W轴增加的方向(从左到右)行进,则对绿色球的倾斜度为负(向下),对于红色球的倾斜度为正(向上)。
仔细阅读下一段,然后根据需要返回到该图。
如果我们希望损失最小,我们希望球到达山谷的最低点。W代表权重和偏差的值,因此,如果我们处于绿色球的位置,我们将减去负导数的一部分(使其为正值)到绿色球的W位置,将其向右移动并减去一部分将红色球的W位置向左移动的正导数(使其变为负数),以使两个球都接近最小值。
从数学上讲,我们有以下内容:
η调整我们用来更新权重和偏差的导数的比例。
现在,继续进行向后传递问题。我将介绍从损失到所有参数的链式导数,我们将看到每种导数代表什么。重要的是要牢记上面介绍的各层的方程式以及它们的参数矩阵。
要记住的一件事是,我们要查找的四个一阶导数数组的形状必须与我们要更新的参数相同。例如,阵列dL / dW_h的形状必须与权重阵列W_h相同。上标T表示矩阵已转置。
我们一直追溯到线性层的参数。因为我们将隐藏状态数组重塑为线性向量,所以我们应将dL / dH ^ t重塑为串联的隐藏状态数组的原始形状。目前,它是一个6 x 1的数组,但从循环图层计算得出的隐藏数组的形状是3 x 2。我们还将所有全局输入连接在一起(t = 1、2和3),现在我们可以继续进行反向传递了。
现在剩下要做的就是应用我们之前看到的Gradient Descent方程来更新参数,并且模型可以进行下一次迭代了。让我们看看如何使用PyTorch构建简单的RNN。
PyTorch的RNN
使用PyTorch非常简单,因为我们真的不需要担心向后传递。但是,即使我们不直接使用它,我仍然相信了解它的工作原理很重要。
继续,如果我们参考PyTorch的文档,我们可以看到它们已经具有可以使用的RNN对象。定义它时,有两个基本参数:
- input_size —输入x中预期要素的数量
- hidden_size —处于隐藏状态h的特征数
input_size为1,因为我们一次使用每个序列的一个时间步长(例如,序列10、20、30中的10),而hidden_size为2,因为我们获得了包含两个值的隐藏状态。
将n_layers参数定义为2意味着我们有一个带有两个隐藏层的堆叠RNN。
另外,我们还将参数batch_first定义为True。这意味着输入和输出中的批次尺寸排在首位(输入和输出不要错)
输入:输入,h_0
- 形状的输入(seq_len,batch,input_size):包含输入序列特征的张量。
- h_0的形状(num_layers * num_directions,batch,hidden_size):张量,包含批次中每个元素的初始隐藏状态。
RNN的输入应该是形状为1 x 3 x 1的输入数组。该序列包含三个时间步长,分别是数据集的第一批10、20和30。从每个批次中,大小为1的输入将作为该序列的三个时间步长被馈送到网络三遍。
隐藏状态h_0是我们的第一个隐藏数组,我们将其与形状为1 x 1 x 2的第一时间步输入一起馈入网络。
输出:输出,h_n
- 形状的输出(seq_len,batch,num_directions * hidden_size):张量,包含每个t的RNN的最后一层的输出特征(h_t)。
- h_n的形状(num_layers * num_directions,batch,hidden_size):张量包含t = seq_len的隐藏状态。
输出包含形状为1 x 3 x 2的每个时间步长由神经网络计算的所有隐藏状态,h_n是最后一个时间步长的隐藏状态。这对于保持有用很有用,因为如果我们选择使用堆叠式递归网络,则这将是隐藏状态,该状态将在第一时间步进给,形状为1 x 1 x 2。
所有这些数组都在上面的示例中表示,并且可以在RNN图中看到。需要注意的另一件事是,使用递归网络和"时间序列预测"的特定示例,将num_directions设置为2将意味着预测未来和过去。此处将不考虑这种类型的配置。
我将在实现RNN以及如何对其进行培训的过程中留下一段代码。我还将将其留给您使用,以根据需要与所需的数据集一起使用。在使用网络之前,请不要忘记规范化数据并创建数据集和数据加载器。
总结思想
为了以一个简短的总结来结束这个故事,我们首先看到了通常使用递归网络解决的两种类型的问题,即时间序列预测和自然语言处理。
后来,我们看到了一些典型配置的示例,以及一个实际示例,其目的是使用多对一配置预测未来的一步。
在前向传递中,我们了解了输入和隐藏状态如何与递归层的权重和偏差交互作用,以及如何使用隐藏状态中包含的信息来预测下一个时间步长值。
反向传递只是链规则的应用,从损失梯度相对于预测的关系到相对于我们要优化的参数的变化。
最后,我们浏览了有关RNN的PyTorch文档的一部分,并讨论了用于构建基本循环网络的最重要部分。
感谢您的阅读!也许您从这个冗长的故事中得到了一些启示。我写它们是为了帮助我理解新概念,并希望也能帮助其他人。
原文链接:https://towardsdatascience.com/rnns-from-theory-to-pytorch-f0af30b610e1