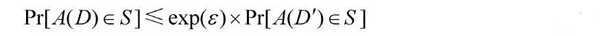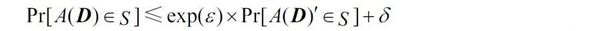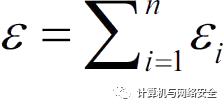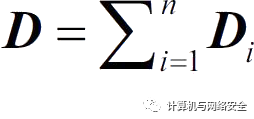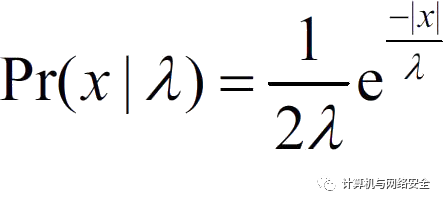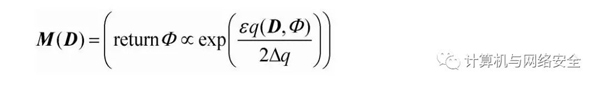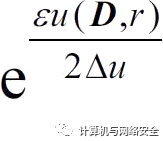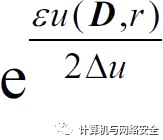物联网会感知大量数据,感知数据通常需要发布和共享。但数据在发布和共享时面临巨大的隐私泄露风险。随着数据挖掘技术的不断提高,经过隐私保护的物联网数据中的敏感信息也越来越容易被数据挖掘者获取,因此,如何保护发布数据中的隐私问题,成为了一个新的研究热点。
从根本上来讲,数据发布隐私保护就是在数据发布的同时,尽可能地保护发布数据中的隐私信息。差分隐私作为目前数据发布隐私保护的一个标准,它能够在数据发布的过程中,对原始数据进行一定的处理,从而达到保护原始数据中敏感信息的目的。简单来说,差分隐私数据发布就是数据拥有者将数据通过某种形式向外界展示,并利用差分隐私技术对数据中的隐私信息进行保护的过程。
01 差分隐私的概念
差分隐私是目前数据发布隐私保护技术中具有强大理论保证和严格数学证明的隐私保护模型。差分隐私保护是对数据添加扰动保护的一种保护技术,它可以不考虑攻击者的背景知识,通过添加一定规律的噪声来保证数据集的统计特征不变,同时也对数据集进行了保护,方便研究者在数据进行保护以后对数据进行一些挖掘、统计工作,不泄露用户的隐私。
差分隐私具有严格的数学证明,该机制可以确保在对数据进行保护以后不会影响输出结果的统计特性,攻击者无法判断该用户是不是在该数据集中,因为使用差分隐私保护以后对于数据的查询结果在形式上不可区分,所以保证了用户的个人隐私信息不被泄露。
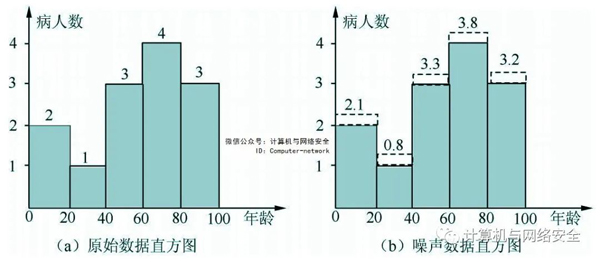
差分隐私可以增加或删除数据库中的一条记录,使得攻击者在具有任何知识背景的情况下都无法判断某条记录是否存在于正在被分析的数据库中。假设存在一个数据表,如图1所示,该数据是某医院的门诊病历记录,其中包括病人的姓名、年龄、性别、临床诊断等信息,图1(a)是原始数据记录的直方图发布形式。如果攻击者想要知道Cole的诊断情况,并且具有强大的背景知识,如攻击者已经知道Cole的性别为男、年龄在60~80岁之间,以及其他人的临床诊断信息,那么攻击者将能够推断出Cole的临床诊断信息,从而导致Cole的隐私信息被泄露。差分隐私想要解决的也正是这类问题,即在攻击者具有任何背景知识的情况下,都不会泄露数据集中的隐私信息。
图1(b)给出了经过差分隐私技术处理过的直方图发布的结果,从图中可以看出,即使攻击者知道年龄在60~80岁之间除了Cole以外所有人的信息,他也没办法获取Cole的诊断信息。
图1 医院门诊病历记录(统计数据直方图发布)
差分隐私:经典的差分隐私(DP)最初是基于数据集提出的隐私保护概念,它可为数据隐私的保护效果提供严格的信息论层次的保证。DP以概率的形式描述原始数据集的微小变化对最终统计输出的影响,并通过隐私参数£来约束这一概率变化,达到隐私保护的目的。
假设D是具有n个记录、d个属性的数据集,并且假设变量r表示数据集中的一条记录。两个数据集D和D′是兄弟数据集,即如果它们有相同的属性,并且只有一个记录不同,令ri表示这个记录,Di表示带有ri记录的数据集,D-i表示删除ri记录的数据集,则差分隐私定义如下。
ε-差分隐私:对于差别至多为一个记录的两个数据集D和D′,Range(A)表示一个随机函数A的取值范围,Pr[Es]表示事件Es的披露风险,若随机函数A提供ε-差分隐私保护,则对于所有的S⊆Range(A),都满足如下所示:
如图2所示,算法通过添加一些规律的噪声来实现差分隐私,同时保证在删除或者添加某一条记录的时候,查询的一些统计概率不发生变化,从而保护了用户之间的隐私信息。
图2 随机算法在邻近数据集上的输出概率
(ε,δ)-差分隐私:对于差别至多为一个记录的两个数据集D和D′,Range(A)表示一个随机函数K的取值范围,Pr[Es]表示事件Es的披露风险,若随机函数A提供(ε,δ)差分隐私保护,则对于所有的S⊆Range(A),都满足如下所示:
其中,D和D′表示相邻数据集,根据相邻数据集的差异,可将差分隐私分为有界差分隐私(Bounded Differential Privacy,BDP)和无界差分隐私(Unbounded Differential Privacy,UDP)。在BDP中,D和D′是相邻数据集,可以通过替代D′中的一个实体而得到D。在UDP中,D和D′是相邻数据集,可以通过添加或删除D′中的一个实体而得到D。BDP中的相邻数据集具有相同的大小,而UDP中却没有这个约束。
(ε,δ)-差分隐私是ε-差分隐私的松弛版本,其允许违反隐私的概率被参数δ控制在一个很小的范围内。这个定义的隐私保护在ε-差分隐私带来过量噪声而导致较低的效用性的场景中,可以展现出明显的优势。
差分隐私能通过添加随机噪声来实现查询操作,这个被添加的噪声是隐私参数ε的一个函数,这个查询的性质被称为敏感度。敏感度的类型会随着两个相邻的数据库的查询结果而改变,在大多数情况下,我们会将全局敏感度作为决定查询结果安全性的一个重要的参数。
ε表示隐私预算,是衡量隐私保护强度的参数。由上图可知,ε值越小,算法的隐私保护程度就越强。反之,隐私保护程度就越弱。差分隐私保证了无论数据库中任意一条记录存在与否,对算法的输出分布几乎没有影响。
相邻数据集:若D与D′为相邻数据集,则D可通过D′添加、删除或修改一个数据元组得到。
从上述定义可以看出,对于任意两个相邻的数据集,它们输出同一结果的概率比率差距介于e-ε和eε之间;由此可知,参数ε对控制隐私泄露量起着至关重要的作用。
基于DP的定义,学者们设计出一些满足要求的随机化机制;在相同的ε水平下,机制的设计和适用性会极大地影响隐私化数据的可用性。
全局敏感度:对于给定的查询函数f:Dn→Rd,f的Lp全局敏感度定义为:
GSf=maxD,D′||f(D)-f(D′)||p
数据集D和D′之间最多相差一条数据记录。
局部敏感度:对于给定的查询函数f:Dn→Rd,其中D∈Dn,D的Lp局部敏感度定义为:
LSf(D)=maxD′|| f(D)-f(D′)||p
对于一些查询操作函数f,得到的∆f都是比较小的,对于计数查询函数来说∆f=1,并且这个属性和查询函数有关,和数据集的属性无关,可以通过这个属性来对数据集进行发布操作,即进行多种函数操作以使数据集满足数据保护要求,一般使用拉普拉斯机制和指数机制进行差分隐私保护。
差分隐私算法具有组合特性,即几个满足差分隐私的独立算法通过组合得到的算法仍满足差分隐私。差分隐私的组合特性保证了一系列差分隐私算法计算的隐私,根据这个特性可得出以下性质。
顺序组合(Sequential Composition):如果一个机制M由多个子机制构成,如M=(M1,M2,…,Mn),其中Mi满足εi-差分隐私,那么机制M满足εi-差分隐私,其中
并行组合(Parallel Composition)。如果数据库中的每个不相交的子集Di在机制Mi下都满足εi-差分隐私,那么
在机制Mi下也满足εi-差分隐私。
02 差分隐私保护模型
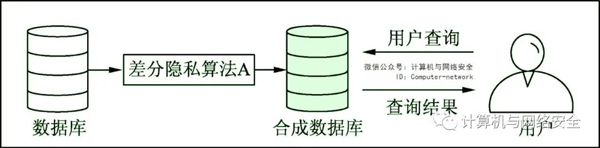
差分隐私数据发布主要有两种保护模型:交互式保护模型和非交互式保护模型。如图3所示,在交互式保护模型下,数据拥有者根据实际需要设计满足差分隐私的数据发布算法A,当用户向服务器发出查询请求Q时,在隐私预算没有消耗完的情况下,返回给用户的查询结果将经过差分隐私算法A添加一定量的噪声,即用户获得的查询结果是添加噪声后的答案,而不是真实答案。这种交互式保护模型具有时效性较好的特点,能够及时更新数据库并实时返回查询结果。但该模型存在的问题就是隐私预算消耗过快,需要利用有限的隐私预算尽可能多地对查询请求进行回答,这其中也涉及如何为每次查询分配隐私预算的问题。
图3 交互式保护模型
图4所示为差分隐私数据发布的非交互式保护模型。数据拥有者首先利用差分隐私算法A对要发布的数据进行隐私保护,然后形成一个新的合成数据库,合成数据库与原始数据库具有相似的统计特征。此时,用户所有的查询以及数据挖掘等操作都是在合成数据库上进行的,以保证原始数据中的隐私信息不被泄露。这种模型的特点就是不限制用户的查询次数,但会导致数据发布的可用性较低、数据查询的时效性较差。
图4 非交互式保护模型
03 差分隐私数据发布机制
任何满足差分隐私定义的机制都可以被看作差分隐私数据发布机制,目前很多差分隐私数据发布机制被提出,如拉普拉斯机制、指数机制、中位数机制、矩阵机制等,但拉普拉斯机制和指数机制是在差分隐私数据发布中应用最广泛的两种机制。这两种机制都可以在满足差分隐私的情况下,对发布的数据进行隐私保护。此外还有敏感数据集发布机制和非敏感数据集发布机制。
(1)拉普拉斯机制
拉普拉斯机制(Laplace Mechanism)适用于输出结果是数值型的查询函数。该机制通过在真实的输出结果中添加合适的拉普拉斯噪声以获得差分隐私,噪声是根据满足概率分布
的拉普拉斯分布LAP(λ)而产生的,其中λ是分布的规模因子,其值取决于全局敏感度∆f和预期的差分隐私变量ε,该分布的方差为σ2=2λ2。下面的定理与定义具体给出了这些变量之间的关系。
对于任意的f:Dn→Rd,当
时,添加满足拉普拉斯分布LAP(λ)的机制的输出结果满足ε-差分隐私。
拉普拉斯机制:若一个机制M满足ε-差分隐私,并且在数据集D上存在一个函数f:D→R,则拉普拉斯机制可表示为:
M(D)=f(D)+LAP(∆/ε)
拉普拉斯机制的原理就是向真实的数据中加入独立的拉普拉斯噪声,该噪声由尺度参数为λ的拉普拉斯概率密度函数产生。如果用LAP(λ)表示拉普拉斯噪声,则拉普拉斯机制有如下定义:
(2)指数机制
对于非数值型数据,差分隐私利用指数机制对结果进行随机化的处理,并用一个打分函数q(D,Φ)来评估输出Φ的质量。另外,由于打分函数依赖于实际的应用,因此不同的应用会有不同的打分函数,这导致没有一个通用的打分函数可以利用。
指数机制(Exponential Mechanism):令q(D,Φ)表示数据集D的一个打分函数,该函数可以度量输出Φ的质量。∆q表示输出Φ的敏感度,当指数机制M满足下式时,其满足差分隐私。
在实际应用中,有许多查询函数的输出结果是非数值型的,这导致添加拉普拉斯噪声没有任何意义。为此,部分学者提出了指数机制以实现非数值型数据的差分隐私保护,并设计了可以获得更好查询响应的应用场景。首先定义一个效用函数u:(D×τ)→R,向输出域R中的输出r中添加实数值噪声。这里,数值越大表示效用性越好。然后以满足
的概率选择一个输出r∈R,其中,∆u=maxD,D′,∀r|u(D,r)−u(D′,r)|是效用函数的敏感度。由于u值越大越容易被选择,因此该机制可以看作对u的最优化。此外,效用函数对数据库中单条记录的改变是不敏感的。
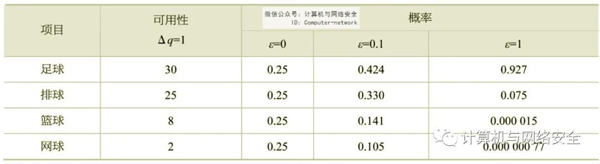
下面给出一个具体的实例来说明指数机制。假如班级举办运动会,需要挑选一个项目来进行比赛,为了保护投票的信息不被泄露,因为最后得到的结果不是数值型的,所以使用指数机制进行保护;对票数进行计数统计时,很显然函数的∆q=1,因此,按照指数机制的要求对表1中的投票结果进行保护,即可算出各个项目的概率值。
表1 指数机制应用实例
从上表的计算结果可以看出,当隐私保护参数比较大的时候,输出结果的概率值也比较大,同时,如果隐私保护参数变小的话,则最后的结果会趋于相等。
对于任意的查询函数u:(D×τ)→R,指数机制以
的概率选择一个输出r时可以保证ε-差分隐私。
(3)敏感候选集发布机制
针对敏感候选集,因为里面包含的不仅是群体用户的行为特征区域,还有用户之间的关联位置信息,所以为了重点保护用户的位置信息不被攻击者推断攻击而泄露用户的位置关联信息,针对敏感候选集提出了关联敏感度差分隐私保护方法,即对差分隐私中的全局敏感度进行改进,进而减少噪声的引入。然后对敏感候选集中的所有聚类簇进行隐私保护,以保护用户的关联位置隐私。上文得到了用户个体的关联敏感度,并且根据得到的敏感候选集的关联属性的强弱可以合理地分配ε的大小,保证数据保护的隐私预算满足差分隐私的要求。针对每个敏感候选集中的用户个体进行个性化重点保护,对于那些关联信息比较强的用户,使用比较强的机制进行数据保护;对于那些关联性比较弱的用户,使用相对弱的机制进行数据保护,进而把用户的关联信息降到一个可接受的范围之内,这样攻击者进行关联攻击的时候,可以得到用户的关联属性的个数就会大大减少。
在处理完用户的敏感候选集以后,得到的数据既保护了用户的位置信息,又保护了用户的关联信息,并且把数据操作转化到了矩阵上进行,这使得算法的复杂度进一步降低。
(4)非敏感候选集发布机制
针对非敏感候选集的用户位置数据,主要是对其中的非停留点位置数据进行隐私保护。用户的非停留点包含了大量的路径问题,如果不加以保护,则会使用户的隐私信息泄露。针对用户轨迹点,虽然其也有一部分的关联信息,但是并没有停留区域表现得那么严重。如果对用户的轨迹点单纯地使用差分隐私的拉普拉斯噪声进行处理,则会在现有的轨迹位置上形成毛刺点,这样很难抵抗攻击者的滤波攻击。因此,这里针对这个问题使用了指数机制,并且在极坐标系下结合用户位置的速度和方向因素来添加相邻位置点的噪声,使得噪声的添加更能保护用户的隐私,对抗滤波攻击。算法主要是针对相邻位置点,计算出下一个点的速度、方向和距离,然后把笛卡尔坐标系转换成极坐标系进行不同维度的噪声添加,这样添加的噪声更加符合现实生活的要求,并且对于攻击者有更好的抵抗能力。这样得到的数据就可以防止攻击者的滤波攻击,使得在添加了保护的基础上还维护了数据集的可用性,还能使得隐私保护和数据集的可用性都有一个很好的平衡。
04 数据发布面临的挑战
目前,虽然许多研究人员致力于数据发布隐私保护技术的研究,但随着信息技术的发展,数据的规模不断增大,数据种类也变得更加复杂多样,尤其是随着数据挖掘技术水平的提高,隐私保护技术在数据发布中的研究意义更加凸显。差分隐私作为数据发布隐私保护技术的标准,对于解决当前数据发布与隐私保护之间的矛盾至关重要。因此,研究更好的差分隐私数据发布方法有着重要的现实意义。综上可知,现有差分隐私数据发布主要面临的挑战如下。
(1)数据类型的变化
目前由于现实生活中的许多应用都倾向于动态的产生并发布数据,与之前相比,数据类型由静态转为了动态,这导致之前提出的许多差分隐私数据发布方法并不适用于当前的动态数据发布。如果用静态数据的发布方法来发布动态数据,就可能会由隐私预算有限而导致发布数据的可用性极差。即使目前已提出一些适用于动态数据发布的差分隐私方法,但动态数据发布的可用性仍有待提高。
(2)隐私预算的分配
在差分隐私数据发布中,隐私预算的分配和数据的发布效用息息相关,尤其在动态数据的发布过程中,如果不能合理分配有限的隐私预算,就可能会导致动态数据发布的效用变差。现有差分隐私动态数据发布方法大部分采用了比较朴素的方法来分配隐私预算,如将隐私预算以均匀、递增或递减的方式分配到需要发布的采样点上,而并没有根据动态数据的特点将有限的隐私预算进行合理的分配,从而导致隐私预算过早耗尽或浪费。因此,如何在动态数据发布中合理分配有限的隐私预算成为了差分隐私动态数据发布面临的一个挑战。