浅析二叉树的层次遍历和最大深度-二叉树的深度优先遍历

在讲解二叉树的时候，提到二叉树的遍历除了前中后序遍历，还有层次遍历。

前中后序这三种遍历方法以及可以通过递归的方式实现了，那么今天就来讲讲层次遍历吧!

LeetCode 第 102题：二叉树的层次遍历

给你一个二叉树，请你返回其按层序遍历得到的节点值。(即逐层地，从左到右访问所有节点)。

示例：  
二叉树：[3,9,20,null,null,15,7],  
#     3 
#   / \ 
#  9  20 
#    /  \ 
#   15   7 
返回其层次遍历结果：  
[ 
 [3], 
 [9,20], 
 [15,7] 
] 
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.

对于这道二叉树题目，我们要遍历每一层的每一个节点，可以考虑分别用BFS(广度优先搜索)和DFS(深度优先搜索)来解决，下面先简单介绍BFS，后续文章继续深入。

有两种通用的遍历树的策略：

深度优先搜索算法(英语：Depth-First-Search，简称DFS)是一种用于遍历或搜索树或图的算法。沿着树的深度遍历树的节点，尽可能深的搜索树的分支。当节点的所在边都己被探寻过，搜索将回溯到发现节点的那条边的起始节点。

深度优先搜索策略又可以根据根节点、左孩子和右孩子的相对顺序被细分为先序遍历，中序遍历和后序遍历。

宽度优先搜索算法(又称广度优先搜索英语：Breadth-First Search, 简称BFS )

我们按照高度顺序一层一层的访问整棵树，高层次的节点将会比低层次的节点先被访问到，最短路径问题常用此算法。

本题就是用广度优先搜索，对二叉树按照层进行搜索，搜索逻辑如下图所示：

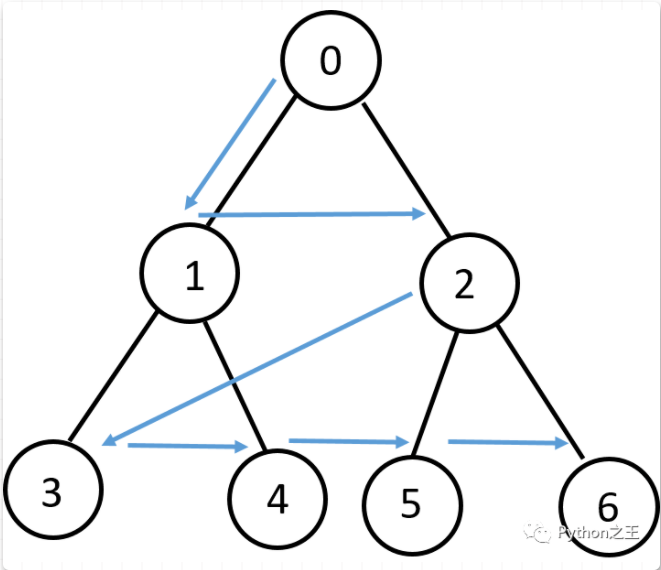
根据我们熟悉的BFS搜索方法，二叉树的层次遍历，关键要用到队列，父结点出，就要判断子结点是否为空，非空则马上进入队列,类似广度优先queue队列。

把每个没有搜索到的点依次放入队列，然后再弹出队列的头部元素作为当前遍历节点，并进行记录。接下来对此节点的所有相邻节点进行搜索，将所有有效且未被访问过的节点压入队列中。

# Definition for a binary tree node. 
# class TreeNode: 
#     def __init__(self, x): 
#         self.val = x 
#         self.left = None 
#         self.right = None 
from collections import deque 
 
class Solution(object): 
    def levelOrder(self, root): 
        res = [] 
        if root is None: 
            return res 
        q = deque([root]) 
        res.append([root.val]) 
        while q: 
            size = len(q) 
            level = [] 
            for i in range(size): 
                node = q.popleft() 
                if node.left != None: 
                    q.append(node.left) 
                    level.append(node.left.val) 
                if node.right != None: 
                    q.append(node.right) 
                    level.append(node.right.val) 
            if level: 
                res.append(level) 
        return res 
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.

LeetCode 第 107题：二叉树的层次遍历II

给定一个二叉树，返回其节点值自底向上的层次遍历。(即按从叶子节点所在层到根节点所在的层，逐层从左向右遍历)

#给定二叉树 [3,9,20,null,null,15,7],  
#     3 
#   / \ 
#  9  20 
#    /  \ 
#   15   7 
# 返回其自底向上的层次遍历为：  
# [ 
#  [15,7], 
#  [9,20], 
#  [3] 
#] 
# Related Topics 树 广度优先搜索 
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.

和LeetCode 第 102题：二叉树的层次遍历完全一样，就是最后的结果改为return res[::-1]

class Solution: 
    def levelOrderBottom(self, root: TreeNode) -> List[List[int]]: 
        res = [] 
        if root is None: 
            return res 
        q = deque([root]) 
        res.append([root.val]) 
        while q: 
            size = len(q) 
            level = [] 
            for i in range(size): 
                node = q.popleft() 
                if node.left != None: 
                    q.append(node.left) 
                    level.append(node.left.val) 
                if node.right != None: 
                    q.append(node.right) 
                    level.append(node.right.val) 
            if level: 
                res.append(level) 
        return res[::-1] 
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.

LeetCode 第 104题：二叉树的最大深度

给定一个二叉树，找出其最大深度。

# 二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。  
# 说明: 叶子节点是指没有子节点的节点。  
# 示例：  
#给定二叉树 [3,9,20,null,null,15,7]，  
#     3 
#   / \ 
#  9  20 
#    /  \ 
#   15   7  
# 返回它的最大深度 3 。  
# Related Topics 树 深度优先搜索 
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.

看到该题目，首先想到的是使用递归来实现，递归的基本条件是访问到根节点(左右子树为空);递归条件是访问左子树或右子树;中间处理逻辑是将子树深度+1，即为最终深度。

# class TreeNode: 
#     def __init__(self, x): 
#         self.val = x 
#         self.left = None 
#         self.right = None 
 
class Solution: 
 # 简化的递归 
 def maxDepth(self, root: TreeNode) -> int: 
        if not root: 
            return 0 
        return max(self.maxDepth(root.left), self.maxDepth(root.right))+1 
 def maxDepth(self, root: TreeNode) -> int:   
  if not root: return 0  
  # 分别得到左右子树的最大深度 
  left = self.maxDepth(root.left)     
  right = self.maxDepth(root.right)     
  return max(left, right) +1 
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.

LeetCode 第 110题：平衡二叉树

给定一个二叉树，判断它是否是高度平衡的二叉树。

# 本题中，一棵高度平衡二叉树定义为：  
# 一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过1。  
# 示例 1:  
# 给定二叉树 [3,9,20,null,null,15,7]  
#     3 
#   / \ 
#  9  20 
#    /  \ 
#   15   7  
# 返回 true 。  
#示例 2:  
# 给定二叉树 [1,2,2,3,3,null,null,4,4]  
# 
#        1 
#      / \ 
#     2   2 
#    / \ 
#   3   3 
#  / \ 
# 4   4 
# 返回 false 。  
# Related Topics 树 深度优先搜索 
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.

定义一个获取当前节点高度的方法, 可以参考上面：求二叉树的最大深度

左右两个子树的高度差的绝对值超过1，则为false

如果当前节点的左右子树满足高度差的绝对值不超过1，则需要继续判断其左右子树分别是否是平衡二叉树。

对于每个节点，左子树和右子树都是平衡树，并且得到左子树和右子树的高度，只要高度差小于1，则为true。

# Definition for a binary tree node. 
# class TreeNode(object): 
#     def __init__(self, x): 
#         self.val = x 
#         self.left = None 
#         self.right = None 
 
class Solution: 
    def isBalanced(self, root: TreeNode) -> bool: 
        if not root: return True 
        return abs(self.depth(root.left) - self.depth(root.right)) <= 1 and \ 
            self.isBalanced(root.left) and self.isBalanced(root.right) 
 
    def depth(self, root): 
        if not root: return 0 
        return max(self.depth(root.left), self.depth(root.right)) +  
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.

但是时间复杂度却是，可以采用DFS(深度优先搜索)

对二叉树做深度优先遍历DFS，递归过程中：
终止条件：当DFS越过叶子节点时，返回高度0;
返回值：从底至顶，返回以每个节点root为根节点的子树最大高度(左右子树中最大的高度值加1 max(left,right) + 1);
当我们发现有一例左/右子树高度差 > 1 的情况时，代表此树不是平衡树，返回-1;
当发现不是平衡树时，后面的高度计算都没有意义了，因此一路返回-1，避免后续多余计算。

最差情况是对树做一遍完整DFS，时间复杂度为 O(N)。

class Solution: 
    def isBalanced(self, root: TreeNode) -> bool: 
        return self.depth(root) != -1 
 
    def depth(self, root): 
        if not root: return 0 
        left = self.depth(root.left) 
        if left == -1: return -1 
        right = self.depth(root.right) 
        if right == -1: return -1 
        return max(left, right) + 1 if abs(left - right) < 2 else -1 
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.

本文已收录 GitHub https://github.com/MaoliRUNsen/runsenlearnpy100更多的文章