本文转载自公众号“读芯术”(ID:AI_Discovery)。
激活函数是人工神经网络的驱动因素,其位于神经元之上,并管理着神经元行为,比如是否需要处理某个输入数据,若需要,又以何种程度处理等等。从技术上来讲,某个节点的激活函数将其在神经网络中前一个节点的数据输入,并输出一个确定值,这个值继而指导后续节点如何发动来响应特定输入信号。
本文剖析由激活函数组成的神经网络,以及神经网络的生物类似物,并简要介绍几种常用的激活函数。
神经网络的结构
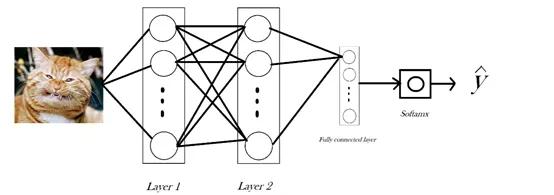
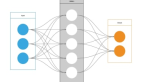
作为一名数据科学爱好者,你一定见过上面的这张图片或者与之相似的图片。这张图片是对双层神经网络工作流程的经典描述。如图,该网络对猫或狗的图片进行分类,其中有两个隐藏层,每一层包含一行神经元,一行有16个。我们把图片局部放大,放大第二层的第一个神经元。
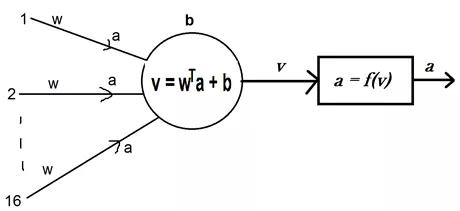
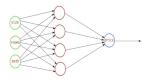
局部放大之后大致如此。注意,此神经元接受前16个神经元传递的信号。神经元将连接权值与信号相乘,并在乘积上加上一个偏差项,最后得到计算结果,并将其命名为v。此v可视为这个神经元对所输入图像的认知。
在识别到输入信号之后,神经元可产生相应的反应,在此激活函数发挥其作用。激活函数被命名为f(),作为由识别到反应的映射,产生值a,并将其传递到下一层神经元,作为前一层特定神经元对信号做出反应的标志。
生物学类比
假如将手放在逐渐升温的钢锅上,一旦温度超过某个阈值,你就会急切地要拿开手。把手移开时并不需要知道锅的确切温度,而是根据实际参数做出选择。这是神经元在放电,当神经元放电时,指令传递到外围(本例中的手)。
这就是激活函数的来源或者至少与之相似。在这里实际数据是冗余的,神经元只需判断其是否超过阈值。
就目前所知,生物神经元和人工神经元之间的一个显著差异是,前者要么被激活,要么不被激活,只有两种结果,而后者的激活程度是在一定范围内。
激活函数的种类
激活函数多种多样。让我们按照函数所解决问题的顺序,大致学习其中的几种:
问题1:学习问题
早期,神经网络的目标是学习自身,线性函数的处理效果相当好。之所以称为线性函数,是因为v = wa + b的近似值与直线方程y = mx + c极为相似。
问题2:非线性问题
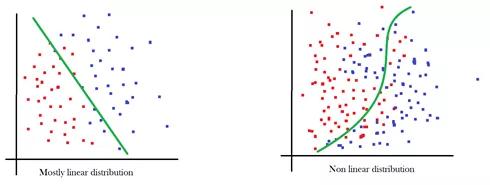
虽然线性函数非常接近于右侧数据,但是左侧数据却效果不佳。由于非线性分布数据集主导着机器学习领域,而且激活函数是将非线性注入到网络中的唯一适用方法,所以函数就不能是线性的。能够解决这个问题的常见函数有:
Sigmoid函数:在函数内输入一个值,输出值的范围为(0,1)。输入的值越小,输出值越接近于0,输入的值越大,输出值则越接近于1,但都不会达到任一个极限值。
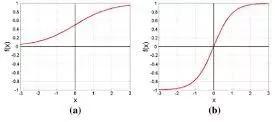
tanh函数:也称双曲正切函数。tanh函数与sigmoid函数非常相似,只是输出值范围为(-1,1)。右侧为sigmoid函数图像,左侧为tanh函数图像。
问题3:梯度消失问题
再次观察图表,sigmoid函数曲线越接近于极限值越平缓,也就是说,当输入绝对值非常大的值的时候,输出值的变化不明显。这大大降低了学习率。这就是所谓的梯度消失问题,随着进程推进,梯度(比如,学习)消失。ReLU函数解决了这个问题,实际上它也是现代神经网络的默认激活函数。
ReLU函数:ReLU函数是线性整流函数(Rectified Linear Unit)的简称,它可能是最有趣、最反直觉的函数。它几乎就是一个直线函数,只不过在原点处有个拐角,所以它是一个分段函数。
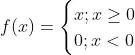
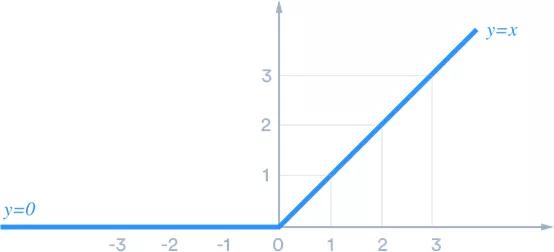
人们经常会问,一个近似线性的函数是如何解决这个问题的。从图中可以明显看出,它几乎可以完全避免梯度消失问题。单个ReLU函数会显得比较单调乏味,但是多个在一些就会变得无懈可击。
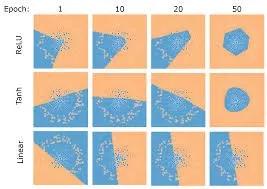
线性函数完全无法近似,而tanh函数试图画出平滑的类圆曲线,所以最终出现了六角形边状的ReLU函数。你可能会认为,这是两个直线的一端接在一起,如同钟表指针那样。
现在,假设有一百万条这样的直线,那么你可以用这种排列方法模拟任何非线性形状。ReLU的精妙之处就在于,它既近似线性,多个组在一起时又能通过改变拐角的角度模拟出几乎所有形状。
这引出了最后一个要解决的问题。
问题4:概率和问题
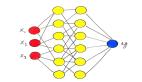
无论隐藏层的工作内容如何,最终的目标都是生成某种预测,而在这里,就是输出一个概率向量,其中包含输入对象为已标记对象概率表。比如,第一张图片中神经网络的结果可能是:
- [dog, cow, cat, goat, lamb] = [0. 2, 0.05, 0.7,0.03, 0.01]
结果最有可能是猫,因为是猫的概率为0.7,概率最高。
为了将全连接层的最终输出值转换为正规化概率向量,需要一个函数接受一个向量,然后输出另一个向量,而且输出向量所有元素的和为1。毕竟,这才是概率向量。
Sigmoid函数非常接近于概率函数,因为它的输出值范围为0到1,但是不满足和等于1的情况。Softmax函数可以满足这一点。
Softmax函数:函数接受一个向量,并使用下列函数计算输出向量中每个元素的相应概率。
函数中分母为所有可能分子的和,避免输出值超过1。
关于激活函数,你了解了嘛?