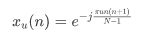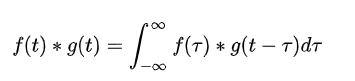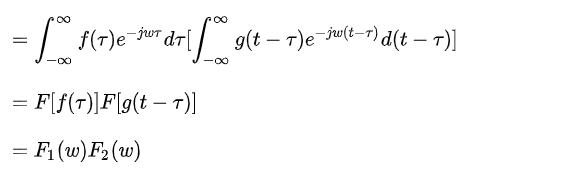在无线通信系统中同步是非常关键的一个过程,这对信号正确的传输有着非常的重要意义。通常,我们常用CAZAC序列(Const Amplitude Zero Auto-Corelation)进行帧同步,CAZAC序列全称恒包络零自相关序列。它主要包括有ZC序列、Frank序列、Golomb多相序列和Chirp序列等。因为其有很好的自相关特性,广泛用于无线通信领域,雷达、CDMA、LTE、5G NR等需要进行信号同步的通信方式。
下面我们以ZC序列为例,利用Python画图来直观的理解这种序列。
ZC序列全称是Zadoff Chu序列,由于其是由Zadoff和Chu提出,所以便由他们的名字来命名,它可以用下面的公式来表示:
式中的u就是它的根。
根据ZC序列的公式,我们就可以方便的画出ZC序列的图形,话不多说,直接撸代码。
- u = 1
- N = 128
- n = np.arange(N)
- x = np.exp(-1j * np.pi*u*n*(n+1)/(N-1))
- plt.subplot(2,1,1)
- plt.plot(np.real(x))
- plt.subplot(2,1,2)
- plt.plot(np.imag(x))
- plt.show()
这里序列根取1,N取128,如下图是它的时域图形,是不是觉得上面的图形看上去似乎有一些规则性。
ZC序列
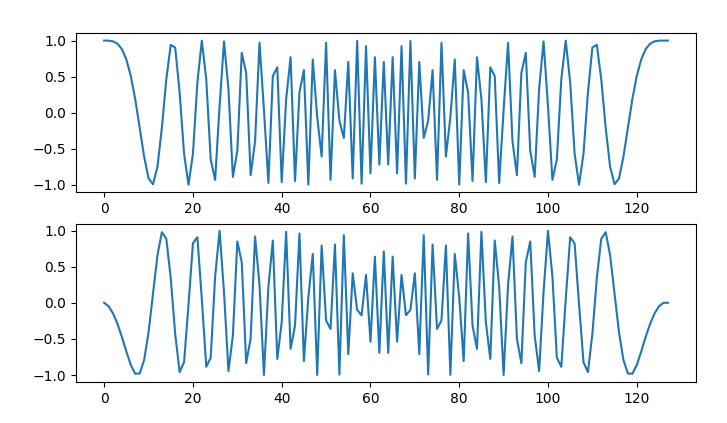
那么,它特别的地方在哪里呀?我们可以换个角度来看这个序列,下面我们在用复数坐标系上把这个序列画出来看看是什么样子。
- u = 1
- N = 128
- n = np.arange(N)
- x = np.exp(-1j * np.pi*u*n*(n+1)/(N-1))
- plt.scatter(np.real(x), np.imag(x))
- plt.show()
图中横坐标为实部I,纵坐标为虚部Q,从图中我们可以看出序列在复平面上是一个圆,也就是说其幅值是恒定的。
复数坐标系下的ZC序列
从序列的公式上看它是一个以e为底的复指数函数,所以大家可以根据之前的文章《谈谈欧拉公式与复指数信号》来理解。
如果把两个序列进行相关运算会发生什么情况呢?关于相关运算实际上就是卷积运算,为了方便计算我们先将序列转到频域进行计算,因为对于时域上卷积运算实际就是频域上相乘,如下卷积计算公式:
将时域进行傅立叶变换:
整理公式得:
推导总是一堆让人头大的公式,不过早就有大佬帮我们总结好了,这里大家需要记住卷积定理即可。
时域卷积定理即时域内的卷积对应频域内的乘积;频域卷积定理即频域内的卷积对应时域内的乘积。
我们继续看下面的代码,我们先将序列向右循环移位10位生成一个新的序列,然后,再用移位后的序列和原序列进行相关运算。
- u = 1
- N = 128
- n = np.arange(N)
- x = np.exp(-1j * np.pi*u*n*(n+1)/(N-1))
- corr = np.fft.fftshift(np.fft.fft(x)) * np.conj(np.fft.fftshift(np.fft.fft(x)))
- plt.subplot(2,1,1)
- plt.plot(np.abs(np.fft.ifftshift(np.fft.ifft(corr))))
- x_r = np.roll(x, 10) #右移
- corr = np.fft.fftshift(np.fft.fft(x_r)) * np.conj(np.fft.fftshift(np.fft.fft(x)))
- plt.subplot(2,1,2)
- plt.plot(np.abs(np.fft.ifftshift(np.fft.ifft(corr))))
- plt.show()
从下面的图中可以发现,在做完相关运算之后会产生一个相关峰,而且相关峰的值非常的大,它的能量较为集中有较好的抗噪能力,除了相关峰外其他位置的相关值都为0或接近于0。而且,经过移位后的序列和原序列进行相关运算之后,相干峰的位置也会向右偏移10位。由于这种相关特性,这里大家也应该清楚了为什么说可以使用这种序列进行帧同步了。
相关运算
如果序列经过傅立叶变换之后,序列的特性又会是什么样呢?
- u = 1
- N = 128
- n = np.arange(N)
- x = np.exp(-1j * np.pi*u*n*(n+1)/(N-1))
- fft_shift = np.fft.fft(x)
- plt.subplot(2,2,1)
- plt.plot(np.real(fft_shift))
- plt.subplot(2,2,2)
- plt.plot(np.imag(fft_shift))
- plt.subplot(2,2,3)
- plt.scatter(np.real(fft_shift), np.imag(fft_shift))
- fft_shift_r = np.roll(fft_shift, 10) #右移
- corr = np.fft.fftshift(np.fft.fft(fft_shift_r)) * np.conj(np.fft.fftshift(np.fft.fft(fft_shift)))
- plt.subplot(2,2,4)
- plt.plot(np.abs(np.fft.ifftshift(np.fft.ifft(corr))))
- plt.show()
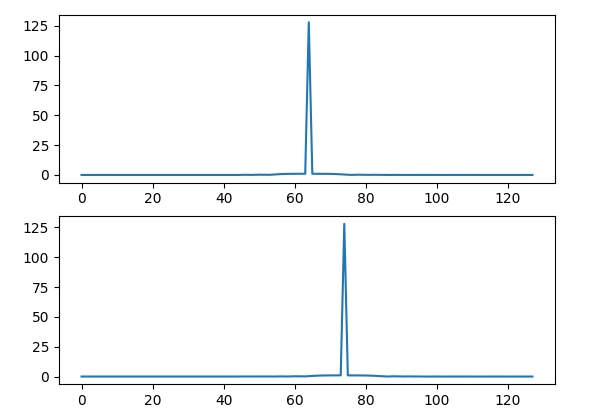
从下图可以看出,结果显而易见,经过傅立叶变换之后的序列仍然具有同样的特性。
傅立叶变换
如果不同根产生的ZC序列进行相关运算会发生什么情况呢?下面我们构造两个根为1和2的ZC序列。
- u1 = 1
- u2 = 2
- N = 128
- n = np.arange(N)
- x1 = np.exp(-1j * np.pi*u1*n*(n+1)/(N-1))
- x2 = np.exp(-1j * np.pi*u2*n*(n+1)/(N-1))
- corr = np.fft.fftshift(np.fft.fft(x2)) * np.conj(np.fft.fftshift(np.fft.fft(x1)))
- plt.plot(np.abs(np.abs(np.fft.ifftshift(np.fft.ifft(corr)))))
- plt.show()
两个不同根序列相关运算后的结果如下图:
不同根序列相关运算
我们从图上看出,对于不同根的序列再进行相关运算之后,不会产生像上面相同根的序列那样会产生又高又细的相关峰。
好了,相信看了上面的几个仿真实验大家都对CAZAC序列有一定的认识。信号处理一个非常抽象的技术,但是大家不要害怕,我们平时需要多多进行实验和练习,才能慢慢的掌握它。
本文转载自微信公众号「Will的大食堂」,可以通过以下二维码关注。转载本文请联系Will的大食堂公众号。