为了表现诚意,先把这句短小精悍的真理放在这里:
神经网络是一种由大量的神经元相互连接构成的运算模型。
很复杂?其实特别简单,相信看完之后,你会感叹一句——不过如此。
神经网络是什么?运算模型。
什么是运算模型?描述如何根据一组输入值计算得出一组输出值的模型。
比如,二元一次方程z=2x+3y+5就是一种运算模型,输入是x和y,输出是z。根据z=2x+3y+5,给定x和y,我们可以得到z,这就是一种运算模型。
注意啦,输出可以是多个值。比如,输入是x和y,输出可以是z1和z2两个值,其中,z1=2x+3y+5,z2=6x+8y+8,这也算是一个运算模型。
神经网络如何表征运算模型?大量的神经元,相互连接。
下图展示了一个神经网络。最左侧的一竖排神经元(蓝色节点)被称为输入层,负责导入输入值。最右侧一竖排神经元(绿色节点)被称为输出层,负责导出输出值。中间两竖排神经元(黑色节点)被称为隐藏层,这些神经元与它们之间的连接一起,共同表征运算模型。
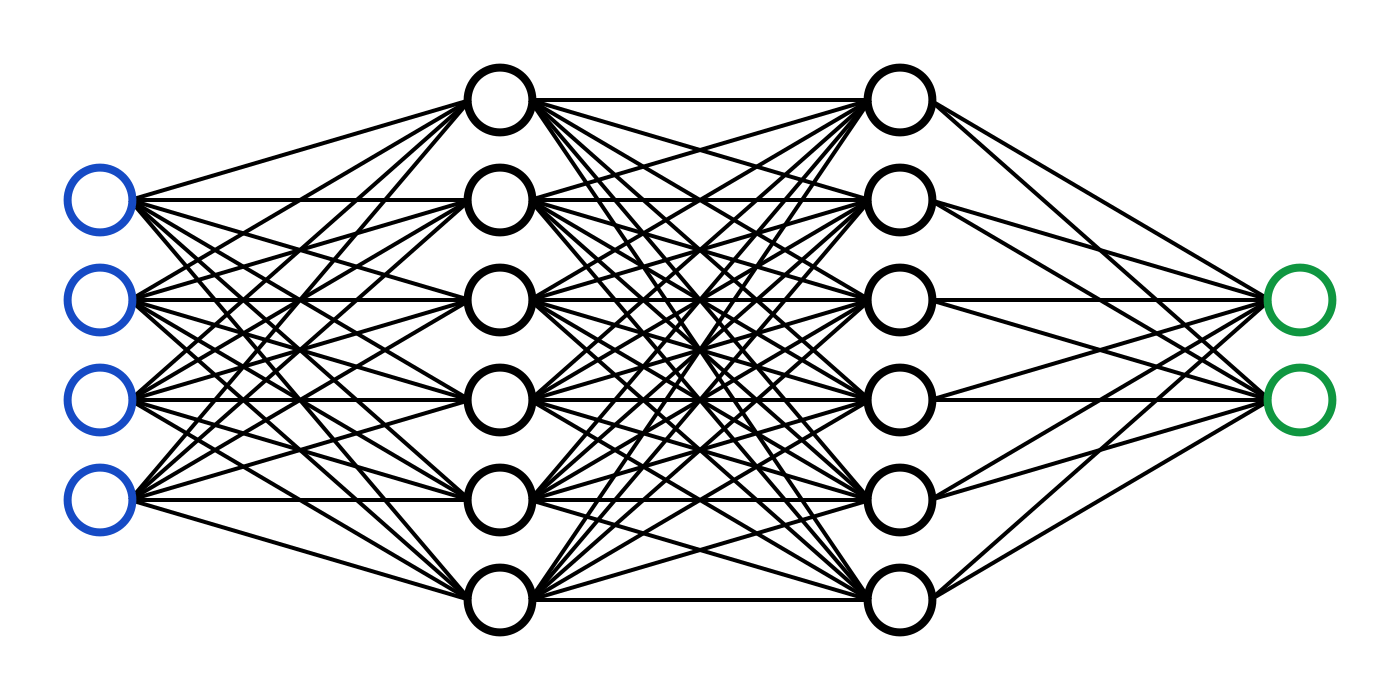
比如,二元一次方程z=2x+3y+5就可以用下图的神经网络表示。
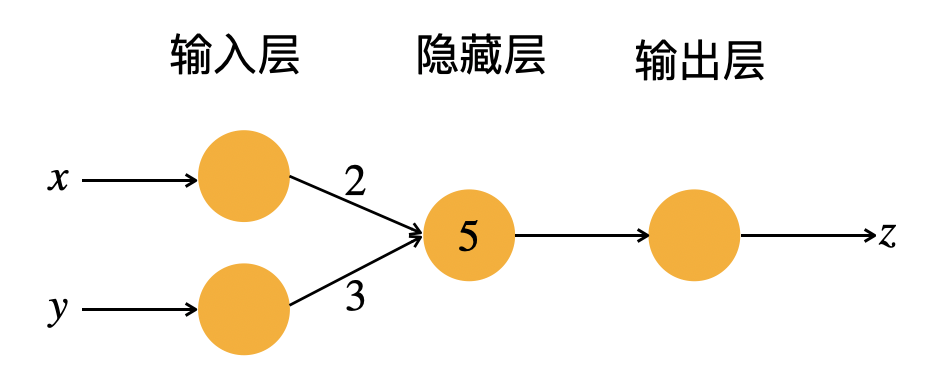
图中,2和3被称为权重值,5被称为偏置值。
一般来讲,只有指向隐藏层神经元的连接(如标有2和3的连接)有权重值,只有隐藏层的神经元(标有5的神经元)有偏置值。权重值和偏移值一般不会被标注在神经网络中。
神经网络中,神经元的数量可以是任意的,神经元之间的连接也可以是多种多样的。
神经元及其连接与数学公式的转换,这里就不具体介绍了。只需要记得,神经网络本质上就是一种运算模型,只要神经元数量足够多,可以表征非常复杂的运算,也就是非常复杂的输入与输出之间的关系。
到这里,「神经网络是一种由大量的神经元相互连接构成的运算模型」这个定义,应该已经很清楚了。
为什么要使用神经网络表征运算模型?直接用数学公式不香吗?
神经网络针对的情况,是我们只知道输入值与输出值,但不知道输入值与输出值的相互关系。比如,我们只知道x=1, y=2时,z=13, 以及x=2, y=1时,z=12,但我们不知道根据x和y计算z的公式。
面对简单的输入输出的关系,我们也许可以直接解方程。但是面对极其复杂的输入输出呢?比如,如果输入是这张图片的像素点,输出是图片中所有的字母。这也是一个典型的图像识别任务。
在这个时候,神经网络是必要的。只要神经网络足够复杂(足够多的神经元,以及适当的神经元连接),我们就可以相信,这个神经网络有能力表征我们希望获得的输入值与输出值的相互关系。
「有能力」意味着,存在特定的权重值和偏置值,使得这个神经网络可以准确的表征输入值与输出值之间的关系。但,我们可能并不知道这些权重值和偏置值。
假设神经网络够有能力了,如何获得权重值和偏置值?
这就要请出人工智能最重要的技术了,机器学习中监督学习!
首先随机猜测权重值和偏置值,之后使用迭代的方式逐步更新这些参数,使得在给定输入值下,神经网络的输出值和实际已知的输出值的差别逐渐减小。直到这个神经网络可以大致准确地表征输入值到输出值的关系,也就是我们所希望获得的运算模型。


































