K聚类是什么意思?
K均值聚类是最流行和广泛使用的无监督学习模型。它也称为群集,因为它通过群集数据来工作。与监督学习模型不同,非监督模型不使用标记数据。
该算法的目的不是预测任何标签。而是更好地了解数据集并对其进行标记。
在k均值聚类中,我们将数据集聚类为不同的组。
这是k均值聚类算法的工作原理
(1) 第一步是随机初始化一些点。这些点称为簇质心。
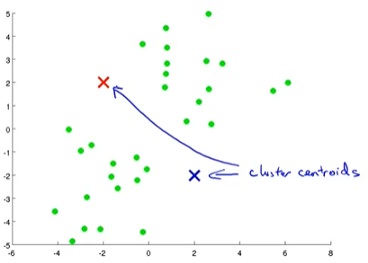
在上图中,红色和蓝色点是群集质心。
您可以选择任意数量的群集质心。但是簇质心的数量必须少于数据点的总数。
(2) 第二步是群集分配步骤。在此步骤中,我们需要遍历每个绿点。根据点是否更靠近红色或蓝色点,我们需要将其分配给其中一个点。
换句话说,根据绿色点是红色还是蓝色来着色,具体取决于它是靠近蓝色簇质心还是红色簇质心。
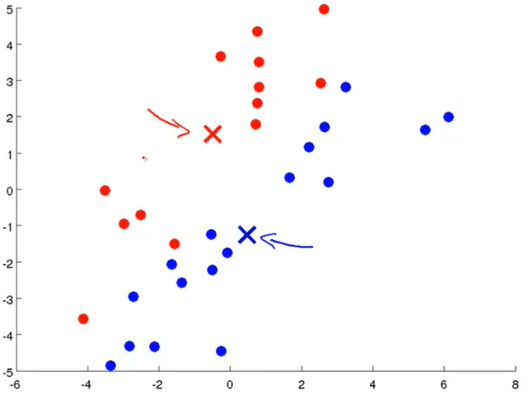
(3) 下一步是移动群集质心。现在,我们必须对分配给红色聚类质心的所有红点取平均值,然后将红色聚类质心移至该平均值。我们需要对蓝色簇质心执行相同的操作。
现在,我们有了新的簇质心。我们必须回到编号2(集群分配步骤)。我们需要将点重新排列到新的群集质心。在那之后重复第三。
数字2和3需要重复几次,直到两个聚类质心都位于合适的位置,如下图所示。
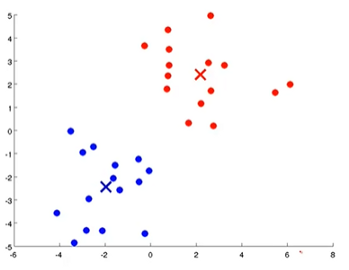
看,我们只是按照分配给它们的簇质心对所有绿色点进行了着色。蓝色簇质心位于蓝色簇的中心,红色簇质心位于红色簇的中心。
当我们开发该算法时,将会稍微清楚一点。我们将对此进行更详细的讨论。
开发算法
我将用于此算法的数据集是从安德鲁·伍(Andrew Ng)在Coursera的机器学习课程中获得的。这是开发k均值算法的分步指南:
(1) 导入必要的包和数据集
- import pandas as pd
- import numpy as np
- df1 = pd.read_excel('dataset.xlsx', sheet_name='ex7data2_X', header=None)
- df1.head()
数据集只有两列。我采用了两个特色数据集,因为它很容易可视化。当您看到视觉效果时,该算法将对您更容易理解。但是,相同的算法也将适用于多维数据集。
我将DataFrame df1转换为Numpy数组,因为我们将在此过程中处理其他数组:
- X = np.array(df1)
现在,我将按照上面讨论的三个步骤进行操作。
(2) 第一步是随机初始化质心。
我将从数据集中随机初始化三个点。首先,我将在0和数据集长度之间选择三个数字。
- import randomrandominit_centroids = random.sample(range(0, len(df1)), 3)
- init_centroids
输出:
- [95, 30, 17]
使用这三个数字作为索引,并获取这些索引的数据点。
- centroids = []
- for i in init_centroids:
- centroids.append(df1.loc[i])
- centroids
输出:
- [0 3.907793
- 1 5.094647
- Name: 95, dtype: float64,
- 0 2.660466
- 1 5.196238
- Name: 30, dtype: float64,
- 0 3.007089
- 1 4.678978
- Name: 17, dtype: float64]
这三点是我们最初的质心。
我将它们转换为二维数组。因为这是我比较熟悉的格式。
- centroids = np.array(centroids)
输出:
- array([[3.90779317, 5.09464676],
- [2.66046572, 5.19623848],
- [3.00708934, 4.67897758]])
(3) 实施群集分配步骤。
在这一步中,我们将遍历数据集中的所有数据点。
一个数据点表示一行数据
让我们看一行数据,了解如何将这些数据分配给集群。
我们将计算所有三个质心的数据距离。然后将该数据点分配给距离最短的质心。
如我们所见,我们必须计算两个点之间的许多距离。让我们开发一个计算距离的函数。
- def calc_distance(X1, X2):
- return(sum((X1 - X2)**2))**0.5
开发一个函数,将每个数据点分配给一个质心。我们的"质心"数组只有三个值。因此,我们有三个索引:0、1、2。我们将为每个数据点分配这些索引之一。
- def findClosestCentroids(ic, X):
- assigned_centroid = []
- for i in X:
- distance=[]
- for j in ic:
- distance.append(calc_distance(i, j))
- assigned_centroid.append(np.argmin(distance))
- return assigned_centroid
此功能是将数据点分配给群集的功能。让我们使用此函数来计算每个数据点的质心:
- get_centroids = findClosestCentroids(centroids, X)
- get_centroids
部分输出:
- [2,
- 0,
- 0,
- 2,
- 1,
- 2,
- 2,
- 2,
- 1,
- 1,
- 2,
- 2,
- 2,
- 2,
- 2,
- 2,
- 0,
总输出很长。因此,我在这里显示部分输出。输出中的第一个质心为2,这意味着将其分配给质心列表的索引2。
(4) 最后一步是根据数据点的平均值移动质心
在这一步中,我们将取每个质心的所有数据点的平均值,然后将质心移动到该平均值。
例如,我们将在索引2处找到分配给质心的所有点的平均值,然后将质心2移至平均值。对索引0和1的质心也执行相同的操作。
让我们定义一个函数来做到这一点:
- def calc_centroids(clusters, X):
- new_centroids = []
- new_df = pd.concat([pd.DataFrame(X), pd.DataFrame(clusters, columns=['cluster'])],
- axis=1)
- for c in set(new_df['cluster']):
- current_cluster = new_df[new_df['cluster'] == c][new_df.columns[:-1]]
- cluster_mean = current_cluster.mean(axis=0)
- new_centroids.append(cluster_mean)
- return new_centroids
这些都是我们需要开发的所有功能。
正如我之前所讨论的,我们需要重复此群集分配过程,并多次移动质心,直到质心处于合适的位置。
对于此问题,我选择重复此过程10次。我将在每次迭代后继续绘制质心和数据,以直观地向您展示其工作方式。
- for i in range(10):
- get_centroids = findClosestCentroids(centroids, X)
- centroids = calc_centroids(get_centroids, X)
- #print(centroids)
- plt.figure()
- plt.scatter(np.array(centroids)[:, 0], np.array(centroids)[:, 1], color='black')
- plt.scatter(X[:, 0], X[:, 1], alpha=0.1)
- plt.show()
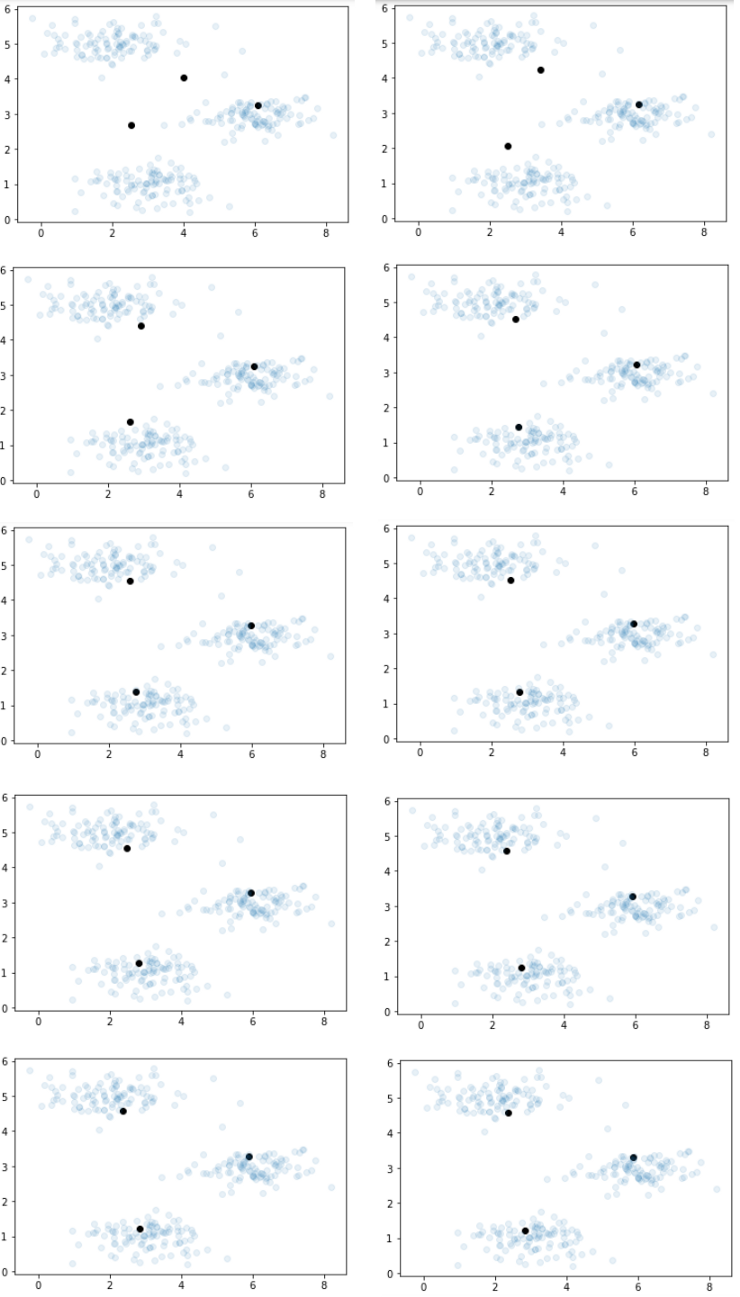
经过五次迭代,将质心设置为其最佳位置。因此,他们此后不再更改职位。
我建议,在尝试降维之前,请运行上面的所有代码以使其学习好。
否则,您可能会感到不知所措!另外,由于我们已经详细解释了该算法,因此我现在将加快执行速度。
降维
我想解释一下这种算法的至少一个用例。一种非常有用的用例是降维。
想一想图像。图像中可能有太多不同的像素。在任何计算机视觉问题中,如果我们可以缩小图片的尺寸,则设备读取该图片的速度将大大提高!是不是
我们可以使用刚刚开发的算法来缩小图片的尺寸。
我将使用青蛙的图片来说明这一点:

> Image By Author
我将这张照片上传到了与笔记本相同的文件夹中。让我们导入这个:
- import cv2
- im = cv2.imread('frog.png')
- im
输出:
- array([[[ 2, 57, 20],
- [ 2, 57, 20],
- [ 2, 57, 21],
- ...,
- [ 0, 5, 3],
- [ 8, 12, 11],
- [ 91, 94, 93]], [[ 2, 56, 20],
- [ 1, 54, 20],
- [ 1, 56, 19],
- ...,
- [ 0, 2, 1],
- [ 7, 9, 8],
- [ 91, 92, 91]], [[ 2, 55, 20],
- [ 2, 53, 19],
- [ 1, 54, 18],
- ...,
- [ 2, 4, 2],
- [ 8, 11, 9],
- [ 91, 93, 91]], ..., [[ 6, 76, 27],
- [ 6, 77, 26],
- [ 6, 78, 28],
- ...,
- [ 6, 55, 18],
- [ 13, 61, 25],
- [ 94, 125, 102]], [[ 9, 79, 31],
- [ 11, 81, 33],
- [ 12, 82, 32],
- ...,
- [ 6, 56, 19],
- [ 14, 61, 27],
- [ 96, 126, 103]], [[ 43, 103, 63],
- [ 44, 107, 66],
- [ 46, 106, 66],
- ...,
- [ 37, 81, 50],
- [ 47, 88, 59],
- [118, 145, 126]]], dtype=uint8)
检查数组的形状,
- im.sgape
输出:
- (155, 201, 3)
我将整个数组除以255,以使所有值从0到1。
然后将其重塑为155 * 201 x 3,使其成为二维数组。因为我们之前开发了二维数组的所有函数。
- im = (im/255).reshape(155*201, 3)
如您在上方所见,有许多不同的像素值。我们要减少它并仅保留10像素值。
让我们初始化10个随机索引,
- randomrandom_index = random.sample(range(0, len(im)), 10)
现在,像上一个示例一样找到质心:
- centroids = []
- for i in random_index:
- centroids.append(im[i])
- centroids = np.array(centroids)
输出:
- array([[0.00392157, 0.21176471, 0.06666667],
- [0.03529412, 0.2627451 , 0.09803922],
- [0.29411765, 0.3254902 , 0.26666667],
- [0.00784314, 0.18431373, 0.05882353],
- [0.29019608, 0.49411765, 0.28235294],
- [0.5254902 , 0.61176471, 0.48627451],
- [0.04313725, 0.23921569, 0.09803922],
- [0.00392157, 0.23529412, 0.0745098 ],
- [0.00392157, 0.20392157, 0.04705882],
- [0.22352941, 0.48235294, 0.40784314]])
现在,我也将" im"转换为数组,
- im = np.array(im)
数据准备就绪。现在,我们可以继续进行集群过程。但是这次,我将不进行可视化。因为数据不再是二维的。因此,可视化并不容易。
- for i in range(20):
- get_centroids = findClosestCentroids(centroids, im)
- centroids = calc_centroids(get_centroids, im)
我们现在得到了更新的质心。
- centroids
输出:
- [0 0.017726
- 1 0.227360
- 2 0.084389
- dtype: float64,
- 0 0.119791
- 1 0.385882
- 2 0.247633
- dtype: float64,
- 0 0.155117
- 1 0.492051
- 2 0.331497
- dtype: float64,
- 0 0.006217
- 1 0.048596
- 2 0.019410
- dtype: float64,
- 0 0.258289
- 1 0.553290
- 2 0.406759
- dtype: float64,
- 0 0.728167
- 1 0.764610
- 2 0.689944
- dtype: float64,
- 0 0.073519
- 1 0.318513
- 2 0.170943
- dtype: float64,
- 0 0.035116
- 1 0.273665
- 2 0.114766
- dtype: float64,
- 0 0.010810
- 1 0.144621
- 2 0.053192
- dtype: float64,
- 0 0.444197
- 1 0.617780
- 2 0.513234
- dtype: float64]
这是最后一步。我们只会保留这10点。
如果还打印get_centroids,您将看到集群分配。
现在,我们要遍历整个数组" im",并将数据更改为其相应的簇质心值。这样,我们将仅具有这些质心值。
我不想更改原始数组,而是要制作一个副本并在那里进行更改。
- imim_recovered = im.copy()
- for i in range(len(im)):
- im_recovered[i] = centroids[get_centroids[i]]
您还记得,我们在一开始就更改了图像的尺寸,使其成为二维数组。我们现在需要将其更改为原始形状。
- im_recoveredim_recovered = im_recovered.reshape(155, 201, 3)
在这里,我将并排绘制原始图像和缩小后的图像,以显示差异:
- im1 = cv2.imread('frog.png')
- import matplotlib.image as mpimg
- fig,ax = plt.subplots(1,2)
- ax[0].imshow(im1)
- ax[1].imshow(im_recovered)

> Image by Author
看,我们如此大地减小了图像的尺寸。不过,它看起来像只青蛙!但是计算机阅读起来会快得多!
结论
在本文中,我解释了k均值聚类的工作原理以及如何从头开始开发k均值聚类算法。我还解释了如何使用此算法来缩小图像尺寸。请尝试使用其他图像。
这是我在本文中使用的数据集的链接。
https://github.com/rashida048/Machine-Learning-With-Python/blob/master/kmean.xlsx
这个是代码:
https://github.com/rashida048/Machine-Learning-With-Python/blob/master/k_mean_clustering_final.ipynb