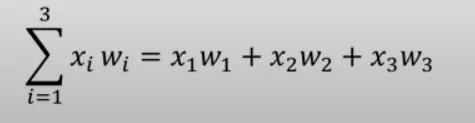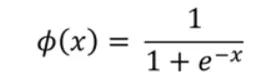本文转载自公众号“读芯术”(ID:AI_Discovery)。
很长时间以来,我一直对构建神经网络跃跃欲试,现在终于有机会来研究它了。我想我并没有完全掌握神经网络背后的数学原理,所以先教人工智能做一些简单的事情吧。
代码原理
神经网络并不是一个新概念,1943年,由沃伦·麦卡洛克(WarrenMcCulloch)和沃尔特·皮茨(Walter Pitts)首次提出。
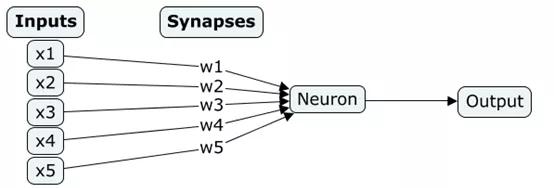
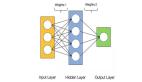
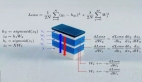
我们将构建一个没有隐藏层或感知器的单层神经网络。它由一个包含训练示例、突触或权重以及神经元的输入层和一个含有正确答案的输出层组成。神经网络图形如下所示:
此外,需要了解一些如sigmoid和导数之类的数学概念,以清楚神经元的学习方式。神经元只需进行简单操作,即取一个输入值,乘以突触权重。之后,对所有这些乘法结果求和,并使用sigmoid函数获得0到1内的输出值。
神经元表示:
Sigmoid函数:
问题界定
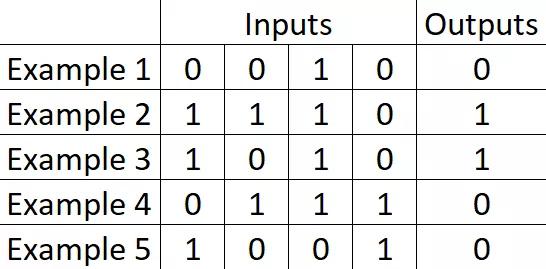
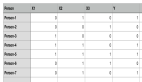
输入层上有数字序列。我们预期的理想结果是,在数据集样本中,如果输入第一个数字是1,则神经网络返回1;如果第一个数字是0,则返回0。结果在输出层中显示。问题集如下图:
先决条件
开始编码的前提——在概念上达到一定程度的理解。
NumPY安装:
- pip install numpy
安装成功,即可进入编码部分。首先,将NumPy导入Python文件中:
- import numpy as np
训练神经网络
首先,创建一个sigmoid函数:
其次,定义训练示例、输入(4×5矩阵)和输出:
接下来,通过生成随机值来初始化突触权重,并将结果排列在4×1的矩阵中:
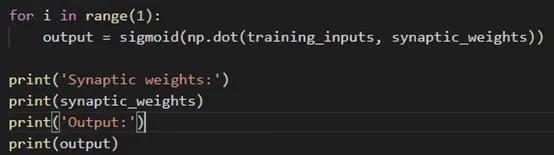
最后,构建训练模型。使用for循环,所有的训练都将在此循环中进行。调用sigmoid函数,并将所有输入的总和乘以sigmoid权重。然后采用Np.dot进行矩阵乘法。过程如下图:
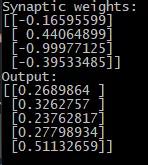
输出结果如下图:
现在进行神经网络模型训练,方法是计算sigmoid函数的输出和实际输出之间的差值。之后可以根据误差的严重性调整权重。多次重复这个过程,比如说一万次。定义sigmoid导数:
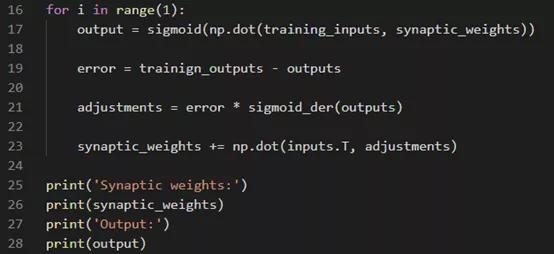
以下是计算和调整权重的方法:
开始学习,观察学习时长会如何影响结果。从100次迭代开始:
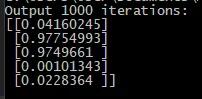
开始情况比较乐观——我们的人工智能已经学会了识别模式,但错误率仍然居高不下。现在进行1000次迭代:
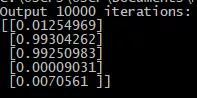
情况好转,继续进行10000次迭代:
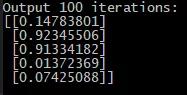
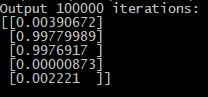
10万次迭代:
我们可以继续更多次的学习迭代,但永远无法达到100%的准确性,因为这需要进行无限次的计算。但即使在最坏的情况下,准确率也达到了99.77%,这相当不错。
对于最终代码,我写得很漂亮,并通过函数将其分开。除此之外,在文本文件中,我还添加了一种非常复杂方法以存储权重。这样只需进行一次学习,而且需要使用AI时,只需导入权重并利用sigmoid函数即可。
- import numpy as np
- from tempfile import TemporaryFile
- def sigmoid(x):
- return 1 / (1 + np.exp(-x))
- def sigmoid_der(x):
- return x * (1 - x)
- def training():
- training_inputs = np.array([[0,0,1,0], [1,1,1,0], [1,0,1,0], [0,1,1,1], [0,1,0,1]])
- trainign_outputs = np.array([[0,1,1,0,0]]).T
- np.random.seed(1)
- synaptic_weights = 2 * np.random.random((4,1)) - 1
- for i in range(50000):
- inputs = training_inputs
- outputs = sigmoid(np.dot(inputs, synaptic_weights))
- error = trainign_outputs - outputs
- adjustments = error * sigmoid_der(outputs)
- synaptic_weights += np.dot(inputs.T, adjustments)
- data_file = open("data.txt", "w")
- for row in synaptic_weights:
- np.savetxt(data_file, row)
- data_file.close()
- def thinking(inputs):
- synaptic_weights = np.loadtxt("data.txt").reshape(4, 1)
- outputs = sigmoid(np.dot(inputs, synaptic_weights))
- print(outputs)
- return outputs
- training()
- thinking(np.array([1,1,0,1]))
图源:Pixabay
我的第一个人工智能已经准备就绪,随时可以投入生产。即使它只能在极小的数据集上识别非常简单的模式,但现在我们可以扩展它,例如,尝试教授人工智能识别图片中的内容。学无止境,精进不休!