神经网络已被开发来模仿人类的大脑。尽管我们还不存在,但是神经网络在机器学习中非常有效。它在1980年代和1990年代很流行。最近,它变得越来越流行。可能是因为计算机足够快,可以在合理的时间内运行大型神经网络。在本文中,我将讨论如何在python中从头开发神经网络算法。
我建议请仔细阅读"神经网络的想法"部分。但是,如果您不太清楚,请不要担心。继续执行部分。我把它分解成小块。同样,您自己运行所有代码将使您更清晰。
神经网络如何工作
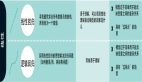
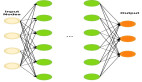
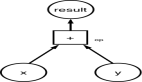
在简单的神经网络中,神经元是基本的计算单元。他们采用输入要素并将其作为输出进行输出。基本的神经网络如下所示:
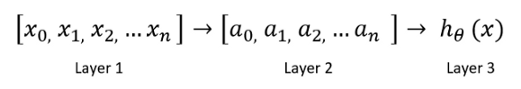
在这里," layer1"是输入功能。"第1层"进入另一个节点layer2,最后输出预测的类别或假设。Layer2是隐藏层。您可以使用多个隐藏层。
您必须根据数据集和准确性要求设计神经网络。
正向传播
从第1层移动到第3层的过程称为前向传播。正向传播的步骤:
(1) 初始化每个输入要素的系数theta。假设有10个输入功能。说,我们有100个培训示例。这意味着100行数据。在这种情况下,我们输入矩阵的大小为100 x10。现在,您确定theta1的大小。行数必须与输入功能的数目相同。在此示例中,该值为10。列数应为您选择的隐藏层的大小。
(2) 将输入要素X与相应的theta相乘,然后添加一个偏差项。通过激活函数传递结果。
有几种可用的激活功能,例如S形,tanh,relu,softmax,swish
我将使用S型激活函数来演示神经网络。
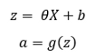
在这里," a"代表隐藏的图层或layer2,而b是偏差。
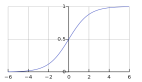
g(z)是S型激活:
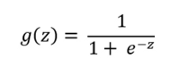
(3) 初始化隐藏层的theta2。大小将是隐藏层的长度乘以输出类的数量。在此示例中,下一层是输出层,因为我们没有更多的隐藏层。
(4) 然后,我们需要遵循与以前相同的过程。将theta和隐藏层相乘,然后通过S型激活层以获取假设或预测输出。
反向传播
反向传播是从输出层移动到layer2的过程。在此过程中,我们计算误差。
(1) 首先,从原始输出y中减去假设。那将是我们的增量。
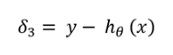
(2) 现在,计算theta2的梯度。将delta3乘以theta2。将其乘以" a2"乘以" 1- a2"。在下面的公式中," a"上的上标2表示layer2。请不要误解它为正方形。
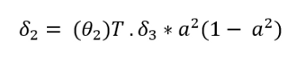
(3) 根据训练样本数m从潜水三角洲计算梯度的非正规化形式。
训练网络
修改theta。将输入要素乘以学习率乘以delta2即可得出theta1。请注意theta的尺寸。

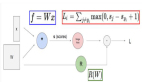
重复正向传播和反向传播的过程,并不断更新参数,直到达到最佳成本为止。这是成本函数的公式。提醒一下,代价函数表示预测距原始输出变量有多远。
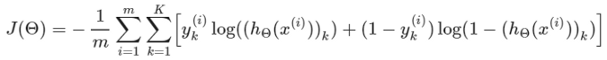
如果您注意到,则此成本函数公式几乎类似于逻辑回归成本函数。
神经网络的实现
我将使用安德鲁·伍(Andrew Ng)在Coursera的机器学习课程中的数据集。可以从以下链接随意下载数据集:
https://github.com/rashida048/Machine-Learning-With-Python/blob/master/ex3d1.xlsx
这是逐步实现神经网络的方法。我鼓励您自己运行每一行代码并打印输出以更好地理解它。
(1) 首先导入必要的包和数据集。
- import pandas as pd
- import numpy as np
- xls = pd.ExcelFile('ex3d1.xlsx')
- df = pd.read_excel(xls, 'X', header = None)
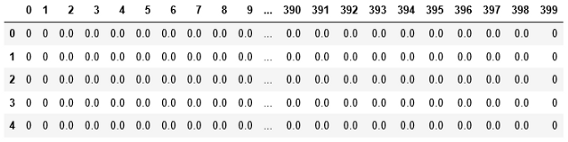
这是数据集的前五行。这些是数字的像素值。请随时下载数据集并遵循:
在此数据集中,输入和输出变量组织在单独的Excel工作表中。让我们将输出变量导入笔记本中:
- y = pd.read_excel(xls, 'y', header=None)

这也是仅数据集的前五行。输出变量是1到10之间的数字。该项目的目标是使用存储在" df"中的输入变量来预测数字。
(2) 查找输入和输出变量的维度
- df.shapey.shape
输入变量或df的形状为5000 x 400,输出变量或y的形状为5000 x 1。
(3) 定义神经网络
为简单起见,我们仅使用25个神经元的一个隐藏层。
- hidden_layer = 25
找出输出类。
- yy_arr = y[0].unique()
- #Output:
- array([10, 1, 2, 3, 4, 5, 6, 7, 8, 9], dtype=int64)
如上所示,有10个输出类。
(4) 初始化θ和偏差
我们将随机初始化layer1和layer2的theta。因为我们有三层,所以会有theta1和theta2。
- theta1的形状:图层1的大小x图层2的大小
- theta2的形状:第2层的大小x第3层的大小
从第2步开始," df"的形状为5000 x400。这意味着有400个输入要素。因此,layer1的大小为400。由于我们将隐藏层的大小指定为25,因此layer2的大小为25。我们有10个输出类。因此,layer3的大小为10。
- theta1的形状:400 x 25
- theta2的形状:25 x 10
同样,将有两个随机初始化的偏置项b1和b2。
- b1的形状:layer2的大小(在这种情况下为25)
- b2的形状:layer3的大小(在这种情况下为10)
定义用于随机初始化theta的函数:
- def randInitializeWeights(Lin, Lout):
- epi = (6**1/2) / (Lin + Lout)**0.5
- w = np.random.rand(Lout, Lin)*(2*epi) -epi
- return w
使用此功能并初始化theta
- hidden_layer = 25
- output =10
- theta1 = randInitializeWeights(len(df.T), hidden_layer)
- theta2 = randInitializeWeights(hidden_layer, output)
- theta = [theta1, theta2]
现在,如上所述,初始化偏差项:
- b1 = np.random.randn(25,)
- b2 = np.random.randn(10,)
(5) 实施正向传播
使用前向传播部分中的公式。
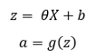
为了方便起见,定义了一个将theta和X相乘的函数
- def z_calc(X, theta):
- return np.dot(X, theta.T)
我们还将使用激活功能几次。还要具有乙状结肠激活功能
- def sigmoid(z):
- return 1/(1+ np.exp(-z))
现在,我将逐步演示正向传播。首先,计算z项:
- z1 =z_calc(df, theta1) + b1
现在通过激活函数传递此z1以获得我们的隐藏层
- a1 = sigmoid(z1)
a1是隐藏层。a1的形状为5000 x25。重复相同的过程以计算layer3或输出层
- z2 = z_calc(a1, theta2) + b2
- a2 = sigmoid(z2)
a2的形状为5000 x10。10列表示10类。a2是我们的layer3或最终输出或假设。如果在此示例中存在更多隐藏层,则将重复执行同一过程以从一层转移到另一层。使用输入要素计算输出层的过程称为前向传播。将它们放到一个函数中,因此我们可以对任意数量的层执行正向传播:
- l = 3 #the umber of layers
- b = [b1, b2]
- def hypothesis(df, theta):
- a = []
- z = []
- for i in range (0, l-1):
- z1 = z_calc(df, theta[i]) + b[i]
- out = sigmoid(z1)
- a.append(out)
- z.append(z1)
- df = out
- return out, a, z
(6) 实施反向传播
这是向后计算梯度并更新theta的过程。在此之前,我们需要修改" y"。" y"有10个班级。但是我们需要将每个类划分到其列中。例如,第一列用于类10。对于其余类,我们将10替换为1,将其替换为0。这样,我们将为每个类创建一个单独的列。
- y1 = np.zeros([len(df), len(y_arr)])
- y1 = pd.DataFrame(y1)
- for i in range(0, len(y_arr)):
- for j in range(0, len(y1)):
- if y[0][j] == y_arr[i]:
- y1.iloc[j, i] = 1
- else:
- y1.iloc[j, i] = 0
- y1.head()
现在,我首先逐步演示正向传播,然后将其全部放入一个函数中,对于反向传播,我将执行相同的操作。使用上面反向传播部分中的梯度公式,首先计算delta3。我们将使用前向传播实现中的z1,z2,a1和a2。
- del3 = y1-a2
现在,使用以下公式计算delta2:
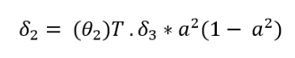
这是delta2:
- del2 = np.dot(del3, theta2) * a1*(1 - a1)
在这里,我们需要学习一个新概念。那是一个S形梯度。S型梯度的公式为:
如果您注意到,这与增量公式中的a(1 — a)完全相同。因为a是sigmoid(z)。因为这是一个约定,所以当我将它们全部组合在一起以编写函数时,我将用此S形梯度代替delta2公式中的a(1-a)项。他们是完全一样的。我只是想演示两个。让我们为S型梯度编写一个函数:
- def sigmoid_grad(z):
- return sigmoid(z)*(1 - sigmoid(z))
最后,是时候使用以下公式更新theta了:
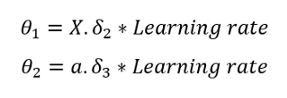
我们需要选择学习率。我选择了0.003。我鼓励您尝试其他学习率,以了解其效果:
- theta1 = np.dot(del2.T, pd.DataFrame(a1)) * 0.003
- theta2 = np.dot(del3.T, pd.DataFrame(a2)) * 0.003
这就是theta需要更新的方式。此过程称为反向传播,因为它向后移动。在编写用于反向传播的函数之前,我们需要定义成本函数。因为我也将成本的计算包括在反向传播方法中。尽管可以在正向传播中添加它,也可以在训练网络时将其分开。这是成本函数的方法
- def cost_function(y, y_calc, l):
- return (np.sum(np.sum(-np.log(y_calc)*y - np.log(1-y_calc)*(1-y))))/m
这里m是训练示例的数量。放在一起:
- y1 = np.zeros([len(df), len(y_arr)])
- y1 = pd.DataFrame(y1)
- for i in range(0, len(y_arr)):
- for j in range(0, len(y1)):
- if y[0][j] == y_arr[i]:
- y1.iloc[j, i] = 1
- else:
- y1.iloc[j, i] = 0
- y1.head()
(7) 训练网络
我将训练网络20个纪元。我将在此代码片段中再次初始化theta。因为我已经使用了theta并对其进行了更新。因此,如果我不再次对其进行初始化,那么我将最终从更新的theta开始。但我想重新开始。
- theta1 = randInitializeWeights(len(df.T), hidden_layer)
- theta2 = randInitializeWeights(hidden_layer, output)
- theta = [theta1, theta2]
- cost_list = []
- for i in range(20):
- theta, cost= backpropagation(df, theta, y1, 0.003)
- cost_list.append(cost)
- cost_list
我使用了0.003的学习率,并将其运行了20个时期。但是请查看下面提供的GitHub链接。我尝试了不同的学习速度和不同的时期,终于到达了这里。
我们获得了在每个时期计算出的成本清单以及最终更新的theta。使用此最终theta预测输出。
(8) 预测输出并计算精度
只需使用假设函数来传递此更新的theta以预测输出:
- out, a, z = hypothesis(df, theta)
现在计算精度,
- accuracy= 0
- for i in range(0, len(out)):
- for j in range(0, len(out[i])):
- if out[i][j] >= 0.5 and y1.iloc[i, j] == 1:
- accuracy += 1
- accuracy/len(df)
精度为100%。完美吧?但是,我们并非始终都能获得100%的准确性。有时,获得70%的准确性非常好,具体取决于数据集。
恭喜!您刚刚开发了完整的神经网络!
结论
对于更简单的分类问题,逻辑回归仍然非常有效!但是对于更复杂的问题,神经网络可以提供更好的结果。如您所见,通过向前和向后传播,它可以更好地学习训练数据。在自然语言处理和图像分类中,神经网络在AI行业中的表现非常出色。
这是Github的完整工作代码链接:
https://github.com/rashida048/Machine-Learning-With-Python/blob/master/NeuralNetworkFinal.ipynb