Logistic回归的两种方法：梯度下降法和优化函数
逻辑回归是一种非常流行的机器学习技术。当因变量是分类的时，我们使用逻辑回归。本文将重点介绍针对多类分类问题的逻辑回归的实现。我假设您已经知道如何使用Logistic回归实现二进制分类。
如果您尚未使用Logistic回归进行二进制分类，那么建议您先阅读本文，然后再深入研究本文。
因为多类分类是建立在二进制分类之上的。
您将在本文中学习二进制分类的概念，公式和工作示例
多类别分类
多类分类的实现遵循与二进制分类相同的思想。如您所知，在二进制分类中，我们解决了是或否问题。就像上述文章中的示例一样，输出回答了一个人是否患有心脏病的问题。我们只有两类：心脏病和无心脏病。
如果输出为1，则该人患有心脏病，如果输出为0，则该人没有心脏病。
在多类别分类中，我们有两个以上的类别。这是一个例子。说，我们具有汽车，卡车，自行车和船的不同特征和特性作为输入特征。我们的工作是预测标签(汽车，卡车，自行车或船)。
如何解决呢?
我们将以解决心脏病或无心脏病的方式将每个类别视为二元分类问题。
这种方法称为"一对多"方法。
在one vs all方法中，当我们使用一个类时，该类用1表示，其余类变为0。
例如，如果我们有四个类别：汽车，卡车，自行车和船。当我们在汽车上工作时，我们将汽车用作1，将其余类别用作零。同样，当我们在卡车上工作时，卡车的元素将为1，其余类别为零。
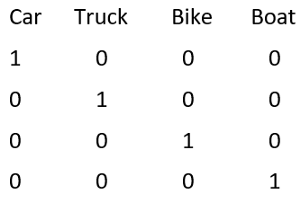
当您将其实现时，它将更加易于理解。我建议您在阅读时继续编码并运行代码。
在这里，我将以两种不同的方式实现此算法：
- 梯度下降法。
- 优化功能方法。
重要方程式及其运作方式：
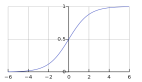
Logistic回归使用S形函数来预测输出。S形函数返回0到1的值。通常，我们采用一个阈值，例如0.5。如果sigmoid函数返回的值大于或等于0.5，则将其视为1;如果sigmoid函数返回的值小于0.5，则将其视为0。
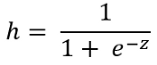
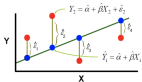
z是输入要素乘以表示为theta的随机初始化值的乘积。
X是输入要素。在大多数情况下，有几种输入功能。因此，此公式变得很大：
X1，X2，X3是输入要素，并且将为每个输入要素随机初始化一个theta。开头的Theta0是偏差项。
该算法的目标是在每次迭代时更新此theta，以便它可以在输入要素和输出标签之间建立关系。
成本函数和梯度下降
成本函数给出的想法是，我们的预测与原始输出相差多远。这是该公式：
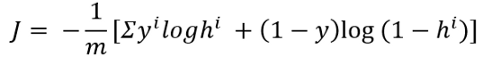
这里：
- m是训练示例数或训练数据数，
- y是原始输出标签，
- h是假设或预测的输出。
这是梯度下降的方程式。使用此公式，我们将在每次迭代中更新theta值：
梯度下降法的实现
先决条件：
- 您需要能够舒适地读取和编写python代码。
- 基本的Numpy和Pandas库。
在这里，我将逐步展示实现。
(1) 导入必要的包和数据集。我从安德鲁·伍(Andrew Ng)在Coursera的机器学习课程中获取了数据集。这是一个手写识别数据集。从1到10的数字。
从像素数据集中，我们需要识别数字。在此数据集中，输入变量和输出变量在Excel文件中的不同工作表中组织。请随时从本页末尾的链接下载数据集。
如果您正在阅读本文，请运行每段代码以学习该算法。
让我们导入必要的包和数据集，
- import pandas as pd
- import numpy as np
- xl = pd.ExcelFile('ex3d1.xlsx')
- df = pd.read_excel(xl, 'X', header=None)
(2) 导入y，它是输出变量
- y = pd.read_excel(xl, 'y', header = None)
(3) 定义采用输入变量和theta的假设。它返回计算出的输出变量。
- def hypothesis(theta, X):
- return 1 / (1 + np.exp(-(np.dot(theta, X.T)))) - 0.0000001
(4) 构建使用输入变量，输出变量和theta的成本函数。它返回假设的成本。这意味着它给出了关于预测距原始输出有多远的想法。
- def cost(X, y, theta):
- y1 = hypothesis(X, theta)
- return -(1/len(X)) * np.sum(y*np.log(y1) + (1-y)*np.log(1-y1))
(5) 现在，该进行数据预处理了。
数据是干净的。不需要太多预处理。我们需要在输入变量中添加一个偏差列。请检查df和y的长度。如果长度不同，则该模型将不起作用。
- print(len(df))
- print(len(y))
- X = pd.concat([pd.Series(1, index=df.index, name='00'), df], axis=1)
(6) y列的数字从1到10。这意味着我们有10个类别。
y是一个不需要的DataFrame。我只会将列保留为包含值的系列。
- yy = y.iloc[:, 0]
我们将为每个类创建与y相同长度的一列。当类为5时，请为该行创建一个包含1的列，否则为5和0。
检查一下，我们有几个类，
- y.unique()
输出：
- array([10, 1, 2, 3, 4, 5, 6, 7, 8, 9], dtype=int64)
因此，我们有10个班级。启动一个具有10列和df.shape [0]行数的DataFrame。
- y1 = np.zeros([df.shape[0], len(y.unique())])
- y1 = pd.DataFrame(y1)
我们将使用一些简单的代码以编程方式进行操作：
- for i in range(0, len(y.unique())):
- for j in range(0, len(y1)):
- if y[j] == y.unique()[i]:
- y1.iloc[j, i] = 1
- else: y1.iloc[j, i] = 0
- y1.head()
(7) 现在定义函数" gradient_descent"。此函数将输入变量，输出变量，θ，alpha和历元数作为参数。在这里，alpha是学习率。
您应该根据需要选择它。太小或太大的学习率可能会使您的算法变慢。我喜欢针对不同的学习率运行该算法，并获得正确学习率的想法。选择正确的学习率可能需要几次迭代。
对于y1中的每一列，我们将实现一个二进制分类。
例如，当我考虑数字2时，数字2应该返回1，其余数字应该返回0。因此，由于我们有10个类，所以每个epoch(iteration)运行了10次。因此，我们在这里有一个嵌套的for循环。
- def gradient_descent(X, y, theta, alpha, epochs):
- m = len(X)
- for i in range(0, epochs):
- for j in range(0, 10):
- theta = pd.DataFrame(theta)
- h = hypothesis(theta.iloc[:,j], X)
- for k in range(0, theta.shape[0]):
- theta.iloc[k, j] -= (alpha/m) * np.sum((h-y.iloc[:, j])*X.iloc[:, k])
- theta = pd.DataFrame(theta)
- return theta, cost
(8) 初始化theta。记住，我们将为每个类实现逻辑回归。每个课程也会有一系列的theta。
我正在运行1500个纪元。我敢肯定，随着时间的推移，准确率会更高。
- theta = np.zeros([df.shape[1]+1, y1.shape[1]])
- theta = gradient_descent(X, y1, theta, 0.02, 1500)
(9) 使用此更新的theta，计算输出变量。
- output = []
- for i in range(0, 10):
- theta1 = pd.DataFrame(theta)
- h = hypothesis(theta1.iloc[:,i], X)
- output.append(h)
- output=pd.DataFrame(output)
(10) 比较计算出的输出和原始输出变量，以计算模型的准确性。
- accuracy = 0
- for col in range(0, 10):
- for row in range(len(y1)):
- if y1.iloc[row, col] == 1 and output.iloc[col, row] >= 0.5:
- accuracy += 1
- accuracyaccuracy = accuracy/len(X)
准确度是72%。我相信，准确度会更高。因为花费了很多时间，所以我没有重新运行算法。
如果您正在运行此程序，请随时尝试更多的纪元，并在注释部分中告知我您的准确度。
除了梯度下降方法外，您还可以使用已经为您内置的优化功能。
在这种方法中，您可以使用优化函数来优化算法的theta。这是一种更快的方法。
具有优化功能的实现
(1) 我们将使用与以前相同的数据集。如果使用相同的笔记本，请使用其他名称导入数据集：
- xls = pd.ExcelFile('ex3d1.xlsx')
- df = pd.read_excel(xls, 'X', header=None)
(2) 我们仍然需要为df中的偏差项添加一列全为1的列。
- X = np.c_[np.ones((df.shape[0], 1)), df]
(3) 导入" y"的数据。
- y = pd.read_excel(xls, 'y', header=None)
由于这是一个DataFrame，因此只需将列零作为一个序列并将其设为二维以将维与X的维匹配。
- yy = y[0]
- yy = y[:, np.newaxis]
在这里，" y"只有一列。将其设为10列，以供10个班级使用。每列将处理一个类。例如，当我们处理类10时，我们将保留10的位置，并将其余值替换为零。这是函数y_change，它将使用y本身和一个类(例如3)。然后它将用其他所有类将1替换为3，将其替换为0。此功能将在以后的步骤中很快使用。
- def y_change(y, cl):
- y_pr=[]
- for i in range(0, len(y)):
- if y[i] == cl:
- y_pr.append(1)
- else:
- y_pr.append(0)
- return y_pr
数据准备完成。现在开发模型：
(4) 定义假设函数。这与以前的方法相同。
- def hypothesis(X, theta):
- z = np.dot(X, theta)
- return 1/(1+np.exp(-(z)))
(5) 开发成本函数。此方法也与以前的方法相同：
- def cost_function(theta, X, y):
- m = X.shape[0]
- y1 = hypothesis(X, theta)
- return -(1/len(X)) * np.sum(y*np.log(y1) + (1-y)*np.log(1-y1))
(6) 定义渐变。这是不同的。此函数定义如何更新theta。
- def gradient(theta, X, y):
- m = X.shape[0]
- y1 = hypothesis(X, theta)
- return (1/m) * np.dot(X.T, y1 - y)
(7) 现在，导入优化函数并初始化theta。我将零作为初始theta值。任何其他值也应该起作用。
- from scipy.optimize import minimize, fmin_tnc
- theta = np.zeros((X.shape[1], 1))
8.让我们做一个拟合函数，将X，y和theta作为输入。它将使用优化函数并为我们输出优化的theta。
它采用以下三个参数：
- 需要最小化的功能
- 要优化的参数，
- 用于优化的参数。
在此示例中，应将成本函数最小化，并且为此需要优化theta。输入和输出变量X和y是要使用的参数。
该优化函数采用另一个参数，即渐变。但这是可选的。在这里，我们有一个用于渐变的公式或函数。因此，我们正在通过它。
- def fit(X, y, theta):
- opt_weigths = fmin_tnc(func=cost_function,
- x0=theta, fprime=gradient,
- args=(X, y.flatten()))
- return opt_weigths[0]
(9) 使用这种拟合方法来找到优化的theta。我们必须分别为每个类优化theta。让我们开发一个函数，其中对于每个类，将在步骤3中使用y_change方法相应地修改" y"。
- def find_param(X, y, theta):
- y_uniq = list(set(y.flatten()))
- theta_list = []
- for i in y_uniq:
- y_tr = pd.Series(y_change(y, i))
- y_try_tr = y_tr[:, np.newaxis]
- theta1 = fit(X, y, theta)
- theta_list.append(theta1)
- return theta_list
使用此方法找到最终theta
- theta_list = find_param(X, y, theta)
(10) 现在是时候预测输出了。我们还必须单独预测类别。
- def predict(theta_list, x, y):
- y_uniq = list(set(y.flatten()))
- y_hat = [0]*len(y)
- for i in range(0, len(y_uniq)):
- y_tr = y_change(y, y_uniq[i])
- y1 = hypothesis(X, theta_list[i])
- for k in range(0, len(y)):
- if y_tr[k] == 1 and y1[k] >= 0.5:
- y_hat[k] = y_uniq[i]
- return y_hat
使用上面的预测方法并计算预测输出y_hat：
- y_hat = predict(theta_list, X, y)
(11) 计算精度
- accuracy=0
- for i in range(0, len(y)):
- if y_hat[i] == y.flatten()[i]:
- accuracy += 1print(accuracy/len(df)*100)
此过程可提供100%的准确性。现在。您可以自己决定要在项目中使用哪种逻辑回归方法。
本文还使用神经网络解决了相同的问题。
检查此GitHub页面以获取数据集：
https://github.com/rashida048/Machine-Learning-With-Python/blob/master/ex3d1.xlsx
