最基本的机器学习算法必须是具有单个变量的线性回归算法。如今,可用的高级机器学习算法,库和技术如此之多,以至于线性回归似乎并不重要。但是,学习基础知识总是一个好主意。这样,您将非常清楚地理解这些概念。在本文中,我将逐步解释线性回归算法。
想法和公式
线性回归使用非常基本的预测思想。公式如下:
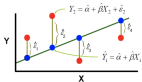
Y = C + BX
我们在学校都学过这个公式。提醒您,这是一条直线方程。在此,Y是因变量,B是斜率,C是截距。通常,对于线性回归,它写为:
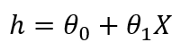
在这里," h"是假设或预测的因变量,X是输入特征,theta0和theta1是系数。Theta值从头开始随机初始化。然后使用梯度下降,我们将更新theta值以最小化成本函数。这是成本函数和梯度下降的解释。
成本函数和梯度下降
成本函数确定预测与原始因变量的距离。这是公式
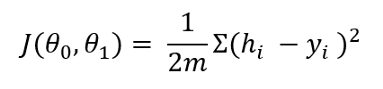
任何机器学习算法的想法都是最小化成本函数,以使假设接近于原始因变量。为此,我们需要优化theta值。如果我们分别基于theta0和theta1取成本函数的偏导数,则会得到梯度下降。要更新theta值,我们需要从相应的theta值中减去梯度下降:
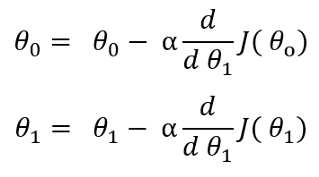
经过偏导数后,以上公式将变为:
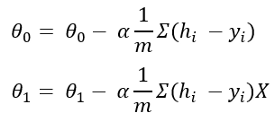
此处,m是训练数据的数量,而alpha是学习率。我正在谈论一种变量线性回归。这就是为什么我只有两个theta值的原因。如果有很多变量,则每个变量都有theta值。
工作实例
我将要使用的数据集来自安德鲁·伍(Andrew Ng)的Coursera机器学习课程。这是在Python中逐步实现线性回归的过程。
(1) 导入包和数据集。
- import numpy as np
- import pandas as pd
- df = pd.read_csv('ex1data1.txt', header = None)
- df.head()
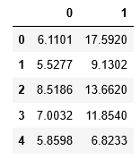
在此数据集中,列零是输入要素,列1是输出变量或因变量。我们将使用列0使用上面的直线公式预测列1。
(2) 将第1列与第0列相对应。
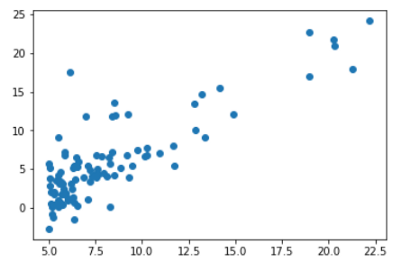
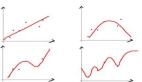
输入变量和输出变量之间的关系是线性的。当关系为线性时,线性回归效果最佳。
(3) 初始化theta值。我正在将theta值初始化为零。但是任何其他值也应该起作用。
- theta = [0,0]
(4) 根据前面讨论的公式定义假设和成本函数。
- def hypothesis(theta, X):
- return theta[0] + theta[1]*X
- def cost_calc(theta, X, y):
- return (1/2*m) * np.sum((hypothesis(theta, X) - y)**2)
(5) 计算训练数据的数量作为DataFrame的长度。然后定义梯度下降函数。在此函数中,我们将更新theta值,直到cost函数达到最小值为止。可能需要任何数量的迭代。在每次迭代中,它将更新theta值,并使用每个更新的theta值来计算成本以跟踪成本。
- m = len(df)
- def gradient_descent(theta, X, y, epoch, alpha):
- cost = []
- i = 0
- while i < epoch:
- hx = hypothesis(theta, X)
- theta[0] -= alpha*(sum(hx-y)/m)
- theta[1] -= (alpha * np.sum((hx - y) * X))/m
- cost.append(cost_calc(theta, X, y))
- i += 1
- return theta, cost
(6) 最后,定义预测函数。它将从梯度下降函数获得更新的theta并预测假设或预测的输出变量。
- def predict(theta, X, y, epoch, alpha):
- theta, cost = gradient_descent(theta, X, y, epoch, alpha)
- return hypothesis(theta, X), cost, theta
(7) 使用预测函数,找到假设,成本和更新的theta值。我选择学习率为0.01,然后将这个算法运行2000个时期或迭代。
- y_predict, cost, theta = predict(theta, df[0], df[1], 2000, 0.01)
最终theta值为-3.79和1.18。
(8) 在同一图中绘制原始y和假设或预测y。
- %matplotlib inline
- import matplotlib.pyplot as plt
- plt.figure()
- plt.scatter(df[0], df[1], label = 'Original y')
- plt.scatter(df[0], y_predict, label = 'predicted y')
- plt.legend(loc = "upper left")
- plt.xlabel("input feature")
- plt.ylabel("Original and Predicted Output")
- plt.show()
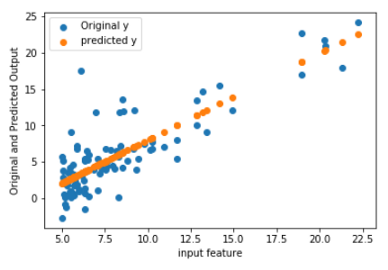
假设图是公式中所预期的一条直线,并且该直线正在最佳位置通过。
(9) 记住,我们在每次迭代中都跟踪成本函数。让我们绘制成本函数。
- plt.figure()
- plt.scatter(range(0, len(cost)), cost)
- plt.show()
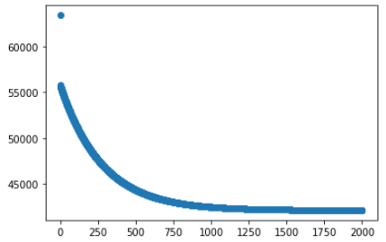
如前所述,我们的目的是优化theta值以最小化成本。从该图可以看出,成本从一开始就急剧下降,然后稳定下来。这意味着theta值已按照我们的预期正确优化。
我希望这可以帮到你。这是本文中使用的数据集的链接:
https://github.com/rashida048/Machine-Learning-With-Python/blob/master/ex1data1.txt。