" 编程的本质来源于算法,而算法的本质来源于数学,编程只不过将数学题进行代码化。"
算法,一门既不容易入门,也不容易精通的学问。
栈和队列都是用来保存数据的,无论底层是使用数组还是链表来实现,其基本原理是不变的,那就是栈的特点的先进后出,队列的特点是先进先出。
栈
栈 (Stack)是一种后进先出(last in first off,LIFO)的数据结构。线性表是用数组来实现的,对于栈这种只能一头插入删除的线性表来说,用数组下标为0(栈底不变,只需要跟踪栈顶的变化即可)的一端作为栈底比较合适。
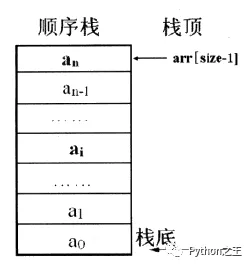
列表封装的这些方法,实现栈这个常用的数据结构比较容易。栈是一种只能在列表一端进出的特殊列表,pop方法正好完美实现:
- In [1]: stack=[1,3,5]
- In [2]: stack.append(0) # push元素0到尾端,不需要指定索引
- In [3]: stack
- Out[3]: [1, 3, 5, 0]
- In [4]: stack.pop() # pop元素,不需指定索引,此时移出尾端元素
- Out[4]: 0
- In [5]: stack
- Out[5]: [1, 3, 5]
由此可见Python的列表当做栈用,完全没有问题,push 和 pop 操作的时间复杂度都为 O(1)
队列
队列(Queue)则是一种先进先出 (fisrt in first out,FIFO)的结构.。使用顺序表存储队列时,队列元素的出队是在队头,即下标为0的地方,当有元素出队时,出队元素后面的所有元素都需要向前移动,保证队列的队头始终处在下标为0的位置,此时会大大增加时间复杂度。

使用列表模拟队列,需要借助Python的collections模块中的双端队列deque实现。如下模拟队列的先进先出,后进后出:
- In [1]: from collections import deque
- In [2]: queue = [1,3,5]
- In [3]: deq = deque(queue)
- In [4]: deq.append(0)
- In [5]: deq
- Out[5]: deque([1, 3, 5, 0]) # 后进插入到队列尾部
- In [6]: deq.popleft()
- Out[6]: 1
- In [7]: deq
- Out[7]: deque([3, 5, 0])# 先进的先出
LeetCode 第 225题:用队列实现栈#使用队列实现栈
- #使用队列实现栈的下列操作:
- # push(x) -- 元素 x 入栈
- # pop() -- 移除栈顶元素
- # top() -- 获取栈顶元素
- # empty() -- 返回栈是否为空
- # 注意:
- # 你只能使用队列的基本操作-- 也就是 push to back, peek/pop from front, size, 和 is empty 这些操作是合法的。
- # 你所使用的语言也许不支持队列。 你可以使用 list 或者 deque(双端队列)来模拟一个队列 , 只要是标准的队列操作即可。
- # 你可以假设所有操作都是有效的(例如, 对一个空的栈不会调用 pop 或者 top 操作)。
- # Related Topics 栈 设计
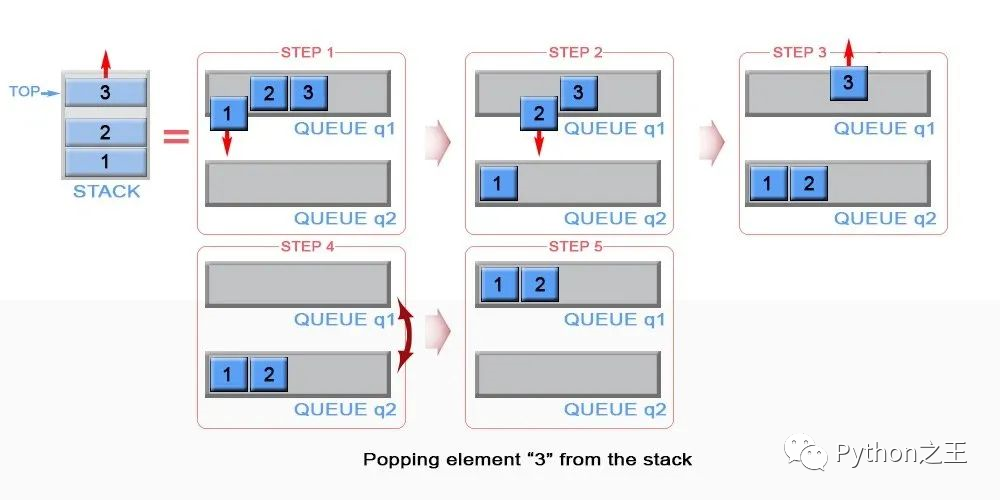
根据题意,我们只能使用队列的基本操作,队列因为是先进先出,要实现先进后出的栈。
无论是用队列实现栈,还是用栈实现队列。常见的解法方法是使用两个队列或者两个栈。
假设有q1,q2两个队列,我们先初始化队列。
- from collections import deque
- class MyStack:
- def __init__(self):
- """
- Initialize your data structure here.
- """
- self.q1 = deque()
- self.q2 = deque()
push(x) :元素 x 入栈 时和队列添加元素的方法一样。
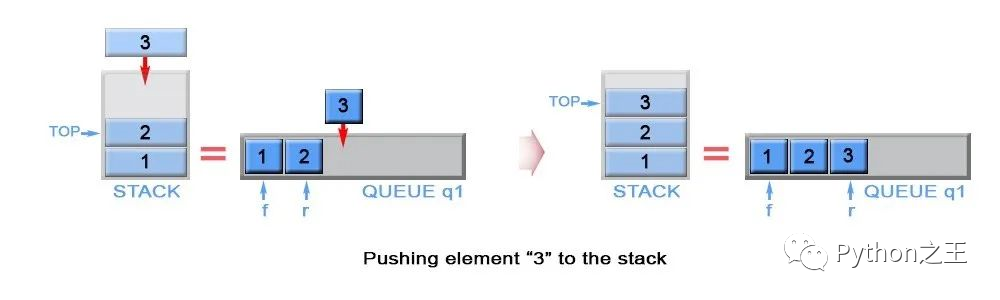
压入栈时,加入到q1的末尾,那么q1末尾的元素就是栈顶元素。因此只需要append(x)即可。
- def push(self, x: int) -> None:
- """
- Push element x onto stack.
- """
- self.q1.append(x)
对于pop删除元素,我们可以使用q2保存q1的最后的元素之前的元素,然后将q1的元素进行删除,最后将两个队列进行互换。
我们需要弹出栈顶元素,也就是q1最后的元素,队列只能是先进先出,我们得用q2把q1出队的元素装着,最后一个出队元素就是栈顶元素。
因此,代码需要对q1的长度进行判断,如果q1的长度大于1,那么将q1的头部元素添加到q2,直到q1只有最后一个元素。
- def pop(self) -> int:
- """
- Removes the element on top of the stack and returns that element.
- """
- while len(self.q1) > 1:
- self.q2.append(self.q1.popleft())
- tmp = self.q1.popleft()
- self.q2, self.q1 = self.q1, self.q2
- return tmp
判断是否为空,只需要判断q1的队列是否为空。
- def empty(self) -> bool:
- """
- Returns whether the stack is empty.
- """
- return not bool(self.q1)
取栈顶元素。这里其实可以巧妙地解决,我们直接调用pop方法进行删除,在pop进行删除时用一个变量进行保存,还需要对该元素重新进行插入操作。
- def top(self) -> int:
- ans = self.pop()
- self.q1.append(ans)
- return ans
下面就是用队列实现栈完整代码
- from collections import deque
- class MyStack:
- def __init__(self):
- """
- Initialize your data structure here.
- """
- self.q1 = deque()
- self.q2 = deque()
- def push(self, x: int) -> None:
- """
- Push element x onto stack.
- """
- self.q1.append(x)
- def pop(self) -> int:
- """
- Removes the element on top of the stack and returns that element.
- """
- while len(self.q1) > 1:
- self.q2.append(self.q1.popleft())
- tmp = self.q1.popleft()
- self.q2,self.q1 = self.q1, self.q2
- return tmp
- def top(self) -> int:
- """
- Get the top element.
- """
- ans = self.pop()
- self.q1.append(ans)
- return ans
- def empty(self) -> bool:
- """
- Returns whether the stack is empty.
- """
- return not bool(self.q1)
LeetCode 第232题:用栈实现队列
- #使用栈实现队列的下列操作:
- # push(x) -- 将一个元素放入队列的尾部。
- # pop() -- 从队列首部移除元素。
- # peek() -- 返回队列首部的元素。
- # empty() -- 返回队列是否为空。
- # 示例:
- # MyQueue queue = new MyQueue();
- #queue.push(1);
- #queue.push(2);
- #queue.peek(); // 返回 1
- #queue.pop(); // 返回 1
- #queue.empty(); // 返回 false
- # 说明:
- # 你只能使用标准的栈操作 -- 也就是只有 push to top, peek/pop from top, size, 和 is empty 操作是合法的。
- # 你所使用的语言也许不支持栈。你可以使用 list 或者 deque(双端队列)来模拟一个栈,只要是标准的栈操作即可。
- # 假设所有操作都是有效的 (例如,一个空的队列不会调用 pop 或者 peek 操作)。
- # Related Topics 栈 设计
最简单的方法使用list表示一个栈,只能使用栈的相关方法,如append(),pop(),s[-1],分别是栈顶追加元素,删除栈顶元素,取出栈顶元素.。
- class MyQueue:
- def __init__(self):
- self.s = []
- def push(self, x: int) -> None:
- self.s.append(x)
- def pop(self) -> int:
- return self.s.pop(0)
- def peek(self) -> int:
- return self.s[0]
- def empty(self) -> bool:
- return not bool(self.s)
当然也可以使用两个栈,这个是比较复杂的操作,「但也是比较常见的算法考点。」
(1)初始化两个栈结构,s1为主栈,s2为辅助栈。
(2)push往s1末尾添加元素,利用append即可实现。
(3)pop时候,先将s1元素向s2转移,知道s1只剩下一个元素时候(这就是我们要返回的队列首部元素),然后我们再把2中的元素转移回s1中即可。
(4)返回队列首部的元素,类似于步骤(3)的操作,唯一不同是这里我们需要将elenment先添加回stack2,然后再将stack2的元素转移回stack1中,因为peek操作不需要删除队列首部元素
(5)empty判断stack1尺寸即可。
出队操作首先判断缓存栈s2是否有元素,有的话直接取出s2栈顶元素;若s2为空并且s1中有元素,将s1中元素全部转移到s2中,再取出s2栈顶元素,即可模拟队列出队操作;本例中没有出现s2和s1都为空的情况。
- class MyQueue:
- def __init__(self):
- """
- Initialize your data structure here.
- """
- self.s1 = []
- self.s2 = []
- def push(self, x: int) -> None:
- """
- Push element x to the back of queue.
- """
- self.s1.append(x)
- def pop(self) -> int:
- """
- Removes the element from in front of queue and returns that element.
- """
- if self.s2:
- return self.s2.pop()
- else:
- if self.s1 :
- while self.s1:
- self.s2.append(self.s1.pop())
- return self.s2.pop()
- def peek(self) -> int:
- """
- Get the front element.
- """
- if self.s2:
- return self.s2[-1]
- else:
- if self.s1 :
- while self.s1:
- self.s2.append(self.s1.pop())
- return self.s2[-1]
- def empty(self) -> bool:
- """
- Returns whether the queue is empty.
- """
- if self.s1 or self.s2:
- return False
- else:
- return True
- # Your MyQueue object will be instantiated and called as such:
- # obj = MyQueue()
- # obj.push(x)
- # param_2 = obj.pop()
- # param_3 = obj.peek()
- # param_4 = obj.empty()
本文已收录 GitHub:
https://github.com/MaoliRUNsen/runsenlearnpy100