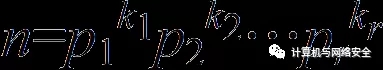微信公众号:计算机与网络安全
ID:Computer-network
传统的加密方法是加密、解密使用同样的密钥,由发送者和接收者分别保存,在加密和解密时使用。采用这种方法的主要问题是密钥的生成、注入、存储、管理、分发等很复杂,特别是随着用户数量的增加,密钥的需求量成倍增加。在网络通信中,大量密钥的分配是一个难以解决的问题。
为了解决常规密钥密码体制的密钥分配问题,满足用户对数字签名的需求,1976年,美国学者Diffie和Hellman发表了著名论文《密码学的新方向》,提出了建立“公开密钥密码体制”:若用户A有加密密钥ka(公开),不同于解密密钥ka′(保密),要求ka的公开不影响ka′的安全;若用户B要向用户A保密传送明文m,则可查用户A的公开密钥ka,若用ka加密得到密文c,则用户A收到c后,用只有用户A自己才掌握的解密密钥ka′对c进行解密以得到m。
1978年,美国麻省理工学院的研究小组成员李维斯特(Rivest)、沙米尔(Shamir)和艾德曼(Adleman)(如图1所示)提出了一种基于公钥密码体制的优秀加密算法——RSA算法。RSA算法是第一个比较完善的公开密钥算法,它既能用于加密,也能用于数字签名。RSA算法以它的三个发明者Rivest,Shamir,Adleman的名字首字母命名,这个算法经受住了多年深入的密码分析。密码分析者既不能证明也不能否定RSA算法的安全性,但这恰恰说明该算法有一定的可信性。目前,RSA算法已经成为最流行的公开密钥算法。
图1 RSA公开密钥算法的发明人
注:从左到右依次为李维斯特、沙米尔和艾德曼,照片拍摄于1978年
1、RSA算法原理
RSA是最著名且应用最广泛的公开密钥算法,可以同时用于加密和数字签名。国际标准化组织(International Organization for Standardization,ISO)在1992年颁布的国际标准X.509中,将RSA算法正式纳入国际标准。1999年,美国参议院通过立法,规定了数字签名与手写签名的文件、邮件在美国具有同等的法律效力。
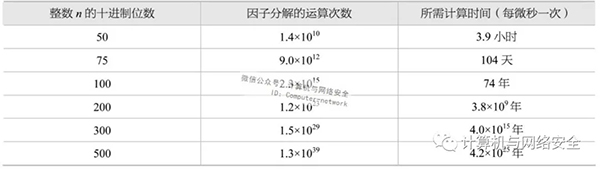
RSA算法是一种分组密码体制算法,它的保密强度是建立在具有大素数因子的合数上的,其因子分解较困难。RSA算法的公钥和私钥选择一对大素数(100到200位十进制数或更大的数)的函数。而从一个公钥和密文恢复出明文的难度,等价于分解两个大素数之积(这是公认的数学难题),但是否为NP问题尚不确定。表1给出了大数分解难度的例子。
表1 大数分解难度举例
RSA算法体制包括:一个公开密钥KU={e,n},一个私有密钥KR={d,n}。其公钥、私钥的组成以及加密、解密的公式如表2所示。
表2 RSA算法
① 有可能找到e、d、n的值,使得对所有的M
② 对于所有的M
③ 在给定e和n时,计算出d是不可行的。
(1)RSA算法的数论基础
下面介绍RSA算法中需要使用的几个术语。
1)素数
素数又称为质数,是指在大于1的自然数中,除了1和此数自身外,不能被其他自然数整除的数。例如,15=3×5,所以15不是素数;又如,12=6×2=4×3,所以12也不是素数。而13除了等于13×1以外,不能再表示为其他任何两个整数的乘积,所以13是一个素数。
2)互为素数
公约数只有1的两个自然数,叫作互质数,即互素数。两个自然数是否互为素数的判别方法主要有以下8种(不限于此)。
① 两个质数一定是互质数,例如,2与7,13与19。
② 一个质数如果不能整除另一个合数,那么这两个数为互质数,例如,3与10,5与26。
③ 1不是质数也不是合数,它和任何一个自然数都是互质数,例如,1和9908。
④ 相邻的两个自然数是互质数,例如,15与16。
⑤ 相邻的两个奇数是互质数,例如,49与51。
⑥ 大数是质数的两个数是互质数,例如,97与88。
⑦ 小数是质数,大数不是小数的倍数的两个数是互质数,例如,7与16。
⑧ 两个数都是合数(两数之差又较大),小数所有的质因数都不是大数的约数,这两个数是互质数。例如,357与715,357=3×7×17,而3、7和17都不是715的约数,所以这两个数为互质数。
3)模运算
模运算是整数运算,有一个整数m,以n为模做模运算,即mmod n。令m被n整除,只取所得的余数作为结果,就叫作模运算。例如,10 mod 3=1,26 mod 6=2,28 mod 2=0等。
模运算有以下性质。
① 同余性:若amod n=bmod n,则正整数a与b同余。
② 对称性:若a=b mod n,则b=amod n。
③ 传递性:若a=b mod n,b=cmod n,则a=cmod n。
4)Euler函数
任意给定正整数n,计算在小于或等于n的正整数之中有多少个与n能构成互质关系的方法叫作欧拉函数,以φ(n)表示。例如,φ(8)=4,这是因为在1~8之中与8能形成互质关系的数有4个:1,3,5,7。
φ(n)的计算方法并不复杂,下面分情况对其进行讨论。
第一种情况:如果n=1,则φ(1)=1,因为1与任何数(包括其自身)都能构成互质关系。
第二种情况:如果n是素数,则φ(n)=n-1,因为质数与每个小于它的数都能构成互质关系。
第三种情况:如果n是素数的某一个次方,如n=pk,p为素数,k≥1,则
φ(pk)=pk-pk-1
例如,φ(8)=φ(23)=23-22=4。这是因为只有当一个数不包含素数p时,才能与n互质。而包含素数p的数一共有pk-1个,即1×p、2×p、…、pk-1×p。
第四种情况:如果n可以分解成两个互质的整数之积,例如,n=p1×p2,则φ(n)=φ(p1p2)=φ(p1)φ(p2),即积的欧拉函数等于各个因子的欧拉函数之积。例如,φ(56)=φ(7×8)=φ(7)×φ(8)=6×4=24。
第五种情况:对于任意大于1的整数,若其可以写成一系列素数的积,如
,则有
。
5)欧拉定理
如果两个正整数a和n互质,则n的欧拉函数φ(n)满足:
aφ(n)≡1(mod n)
即a的φ(n)次方减去1,被n整除。例如,3和7互质,φ(7)=6,(36-1)/7=104。
如果正整数a与质数p互质,则因为φ(p)=p-1,所以欧拉函数可写成:
ap−1≡1(mod p)
这就是著名的费马小定理(Fermat Theory)。
6)费马小定理
若m是素数,且a不是m的倍数,则am-1 mod m=1。或者,若m是素数,则ammod m=a。例如,46mod 7=4096 mod 7=1,47mod 7=16384 mod 7=4。
推论:对于互素的a和n,有aφ(n)mod n=1。
(2)素数的产生与检验
首先来介绍素数的简单判定算法。在C程序设计中,素数的判定算法为:给定一个正整数n,用2到sqrt(n)之间的所有整数去除n,如果可以整除,则n不是素数,如果不可以整除,则n是素数。这个算法的时间复杂度为O(sqrt(n)),算法描述简单,实现也不困难。但是,这个算法对于位数较大的素数判定就显得力不从心了。
目前,适用于RSA算法的最实用的素数产生办法是概率测试法。该法的思想是随机产生一个大奇数,然后测试其是否满足条件,若满足,则该大奇数可能是素数,否则,其是合数。
由于素数有无穷多个,因此判定一个整数是不是素数一直是一个大难题,威尔逊定理(Wilson's Theorem)就是其中的一种判定方法。
威尔逊定理:若正整数n>1,则n是一个素数当且仅当(n-1)! ≡ -1(mod n)。
虽然说威尔逊定理给出了素数的等价命题,但是由于阶乘的增长速度太快(如13!为60多亿),因此其实际操作价值不高。由此提出了概率检验方法。
米勒-拉宾素性检验(Miller-Rabin Prime Test)是一种典型的概率检验方法。可以证明单次Miller-Rabin的正确概率大于3/4,我们重复若干次就可以增大这个概率。Miller-Rabin虽然有一定的概率出错,但实践证明,在重复20次的情况下,107以内的质数不会判断出错。
2、RSA加解密算法过程
(1)RSA加密算法过程
RSA加密算法的过程如下:
① 取两个随机大素数p和q(保密);
② 计算公开的模数n=p×q(公开);
③ 计算秘密的欧拉函数φ(n)=(p-1)×(q-1)(保密),丢弃p和q,不要让任何人知道;
④ 随机选取整数e,使其满足gcd(e,φ(n))=1(公开e加密密钥);
⑤ 计算d,使其满足de≡1(mod φ(n))(保密d解密密钥);
⑥ 将明文X按模为r自乘e次幂以完成加密操作,从而产生密文Y(X、Y值在0到n-1范围内),即Y=Xemod n;
⑦ 解密,将密文Y按模为n自乘d次幂,得X=Ydmod n。
在RSA加(解)密算法实现过程中,主要的运算量是计算模的逆元以及模指数,通常情况下,计算模的逆元时会采用扩展的欧几里德算法。
(2)RSA解密算法过程
由于指数较大,因此RSA解密过程比较耗时,但利用孙子定理(Chinese Remainder Theorem,CRT)可提高解密算法效率。CRT对RSA解密算法生成两个解密方程(利用M=Cdmod pq),即:M1=Mmod p=(Cmod p)d mod (p-1)mod p,M2=Mmod q=(Cmod q)d mod (q-1)mod q。
解方程M=M1mod p和M=M2mod q,可求得其具有唯一解。
3、RSA算法应用
(1)RSA用于数字签名
① 签名:对任意消息m∈M,用户使用自己的私钥签名如下:S≡md(mod n),进而可以得到签名的消息(m, S)。
② 验证签名:由该用户的公开密钥(e, n),验证m≡Se(mod n)是否成立。
(2)RSA加密算法实例
可以通过一个简单的例子来理解RSA的工作原理。为了便于计算,在以下实例中只选取小数值的素数p, q以及e,假设用户A需要将明文“key”通过RSA加密后传递给用户B,过程如下。
1)设计公私密钥(e,n)和(d,n)
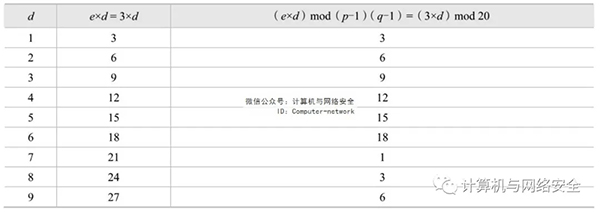
令p=3,q=11,得出n=p×q=3×11=33;f(n)=(p-1)(q-1)=2×10=20;取e=3(3与20互质),则e×d≡1 mod f(n),即3×d≡1 mod 20。d的取值可以用试算的办法来确定。试算结果如表3所示。
表3 d的取值试算结果
通过试算得出,当d=7时,e×d≡1 mod f(n)同余等式成立。因此,可令d=7,从而可以设计出一对公私密钥,加密密钥(公钥)为:KU=(e,n)=(3,33),解密密钥(私钥)为:KR=(d,n)=(7,33)。
2)英文数字化
将明文信息数字化,并将其以每块两个数字进行分组。假定明文英文字母编码表为按字母顺序排列的数值,如表4所示。
表4 明文英文字母编码表
则可得到分组后的key的明文信息为:11,05,25。
3)明文加密
用户加密密钥(3,33)将数字化明文分组信息加密成密文。由C≡Me(mod n)得:
C1=(M1)d(modn)=113(mod33)=11
C2=(M2)d(modn)=053(mod33)=26
C3=(M3)d(modn)=253(mod33)=16
因此,得到相应的密文信息为:11,26,16。
4)密文解密
用户B收到密文后,若要将其解密,则只需要计算M≡Cd(mod n),即:
M1=(C1)d(modn)=117(mod33)=11
M2=(C2)d(modn)=317(mod33)=05
M3=(C3)d(modn)=167(mod33)=25
用户B得到的明文信息为:11,05,25。根据上面的编码表将其转换为英文,即可得到恢复后的原文“key”。
当然,实际运用要比这复杂得多。由于RSA算法的公钥私钥的长度(模长度)须达到1024位甚至2048位才能保证安全,因此,p、q、e的选取、公钥私钥的生成、加密解密模指数的运算都有一定的计算程序,需要依赖计算机的高速计算能力来完成。
4、RSA加解密算法的安全性
在RSA密码应用中,公钥KU是被公开的,即e和n的数值可以被第三方窃听者得到。破解RSA密码的关键在于从已知的e和n的数值(n等于pq)中求出d的数值,从而得到私钥以破解密文。从上文中的公式:d≡e-1(mod((p-1)(q-1)))或de≡1(mod((p-1)(q-1)))可以看出,密码破解的实质问题是:从pq这一数值求出(p-1)和(q-1)。换句话说,只要求出p和q的值,就能求出d的值进而得到私钥。
若p和q是大素数,则从它们的积pq去分解因子p和q,就是一个公认的数学难题。例如,当pq大到1024位时,迄今为止还没有人能够利用任何计算工具完成其分解因子这一任务。因此,RSA从被提出到现在40余年,经历了各种攻击的考验,逐渐为人们所接受,被普遍认为是目前最优秀的公钥方案之一。
然而,虽然RSA的安全性依赖于大数的因子分解,但并没有从理论上证明破译RSA的难度与大数分解的难度等价,即RSA的重大缺陷是无法从理论上把握它的保密性能。
此外,RSA的缺点还有:
① 产生密钥很麻烦,会受到素数产生技术的限制,因而难以做到一次一密;
② 分组长度太大,为保证安全性,n至少需要600 bits 以上,运算代价高,速度慢,较对称密码算法慢几个数量级,且随着大数分解技术的发展,这个长度还在增加,不利于数据格式的标准化。
因此,使用RSA只能加密少量数据,大量的数据加密还要依靠对称密码算法。