相比于电子计算,光计算具有高速、高带宽、低功耗的优势,但目前光计算还不够成熟,只在某些特定领域得到了非常有限的应用。近日,Nature 上一篇 Perspective 文章剖析了深度光学和深度光子学的人工智能推理应用,展示了该领域(尤其是光 - 电混合系统)的发展潜力。
为了高速且低功耗地执行各种应用中的人工智能任务,我们需要加速器。光计算系统也许能够满足这些领域特定的需求,但即便已经历半个世纪的研究,通用型光计算系统仍还未发展成一项成熟的实用技术。但是,人工智能推理(尤其是用于视觉计算应用的推理)也许能为基于光学和光子学系统的推理提供机会。
本文将回顾用于人工智能的光学计算的近期研究成果并探讨其潜力和挑战。
计算系统的能力正与它们试图理解的飞速增长的视觉数据进行军备竞赛。在自动驾驶、机器人视觉、智能家居、遥感、显微技术、监控、国防和物联网等多种应用中,计算成像系统都会记录和处理前所未有的巨量数据。对这些数据的解读不可能由人类完成,而是要使用基于人工智能(AI)构建的算法。
在这些应用之中,深度神经网络(DNN)正快速发展成为视觉数据处理的标准算法方法。这主要是因为 DNN 在许多基准上都取得了当前最佳的结果,而且往往超出其它方法一大截。深度学习近来的这些突破性进展主要得益于现代图形处理单元(GPU)的强大处理能力和并行计算能力以及大规模视觉数据集的可用性,这些进展让 DNN 可以高效地使用监督式机器学习策略执行训练。
但是,高端 GPU 和其它运行日趋复杂的神经网络的加速器的功耗和带宽需求非常高,它们需要大量处理时间而且具有尺寸庞大的外形。这些限制让人难以在边缘设备中使用 DNN,比如相机、自动化载具、机器人或物联网外围设备。以自动汽车中的视觉系统为例,其必须要能使用有限的计算资源实时地做出稳定可靠的决策。当汽车在高速行驶时,瞬间的决策关乎人的生死。事实上,如果计算成像系统能做到更精简,那么几乎所有边缘设备都能从中受益,这能带来更低的延迟以及尺寸、重量和功耗方面的改进。
DNN 一般都包含训练和推理两个阶段,这两个阶段的计算需求差异很大。在训练阶段,会向 DNN 输入大量有标注的样本,然后针对某个特定任务,使用迭代方法优化该 DNN 的参数。训练完成后,可使用该 DNN 来执行推理:以前向通过的方式向该网络输入一个数据(比如一张图像),经过该网络处理后计算得到所需结果。虽然某些应用也会使用 GPU 来执行推理,但对许多边缘设备而言,由于前述原因,使用 GPU 并不现实。
尽管电子 AI 加速器很灵活,但光神经网络(ONN)和光子回路可能为该应用与其它机器学习应用带来一次范式转换。光计算系统有望实现大规模的并行计算,同时设备尺寸还更小,而且在某些实现中的功耗非常低。事实上,在计算系统中使用光来实现通信的光互连(optical interconnect)技术已经在现如今的数据中心中得到了广泛应用,而且在计算系统更深处越来越多地使用光互连可能是持续扩展的关键。
不同于电互连技术,随着光学、光电和电子设备的更深度整合,光互连有望为通信的带宽密度和单位比特的能量消耗带来几个数量级的提升和改善。这种改进过的互连技术能实现电 - 光混合 DNN,而且这种低功耗、高并行的集成技术还可用作模拟光处理器的部件。
尽管光计算机潜力巨大而且也已历经约半个世纪的研究,但通用型光计算仍还不是一项成熟的实用技术。但是,推理任务(尤其是用于视觉计算应用的推理任务)已可使用全光学或光 - 电混合系统来很好地实现。举个例子,线性光学元件可以近乎「免费」地计算卷积、傅立叶变换、随机投影和许多其它运算,因为这些运算可作为光与物质交互或光传播的副产物。这些运算是 DNN 架构的基本构建模块,驱动着大多数现代视觉计算算法。我们有望以光速执行这些运算,同时功耗需求很低乃至没有。本文认为这具有变革性的潜力。
回顾光计算的历史
下图 1 展示了人工智能及相关光学和光子学实现的时间轴。其中展示了一些经过挑选的里程碑和论文,并重点关注了近期进展。
以具体年份计则如下所示:
- 1949 年,Donald O. Hebb 发表《行为的组织(The Organization of Behavior)》一书
- 1957 年,Frank Rosenblatt 提出感知器
- 1960 年,Widrow & Hoff 提出自适应开关电路
- 1964 年,Lugt 提出光学相关性(Optical correlation)
- 1982 年,John Hopfield 提出 Hopfield 网络;Kohonen 提出自组织特征图
- 1984 年,Goodman et al. 发表论文《用于超大规模集成电路系统的光互连(Optical interconnections for VLSI systems)》
- 1985 年,Farhat et al. 发表论文《Hopfield 模型的光学实现(Optical implementation of the Hopfield model)》
- 1986 年,Rumelhart et al. 提出使用反向传播的多层感知器
- 1990 年,LeCun et al. 使用 CNN 实现数字字符识别;Psaltis et al. 使用非线性光反应晶体的光神经网络(ONN)
- 2006 年,Hinton & Salakhutdinov 提出深度自编码器
- 2012 年,Krizhevksy et al. 提出深度 CNN
- 2017 年,Shen et al. 提出使用纳米光子电路的深度学习;Tait et al. 提出神经形态光子网络
- 2018 年,Chang et al. 提出光 CNN;Lin et al. 提出全光衍射神经网络
- 2019 年,Feldman et al. 提出高带宽光子神经突触网络
用于人工智能的光子回路
现代 DNN 架构是级联的线性层后面跟着非线性激活函数,而且这会重复很多次。最一般形式的线性层是全连接层。在这种情况下,每个输出神经元都是所有输入神经元的加权和。从数学上看,这可以表示成一种矩阵 - 向量乘法,从而可以有效地使用光学技术实现。也就是说我们可以使用光子回路来执行人工智能的相关计算。不过相关技术还面临着可编程性等有待解决的问题。
使用自由空间、透镜和复杂介质进行计算
还有一种可替代光子回路的选择:在自由空间或某种介质中传播的光场上直接构建计算能力。(见下图 2)从数学上讲,在自由空间中传播的波可用基尔霍夫衍射积分(Kirchhoff’s diffraction integral)来描述,这相当于让该场与一个固定的核(kernel)执行卷积。该运算又是卷积神经网络(CNN)的一大基本构建模块,而 CNN 又是最常用的视觉计算框架。
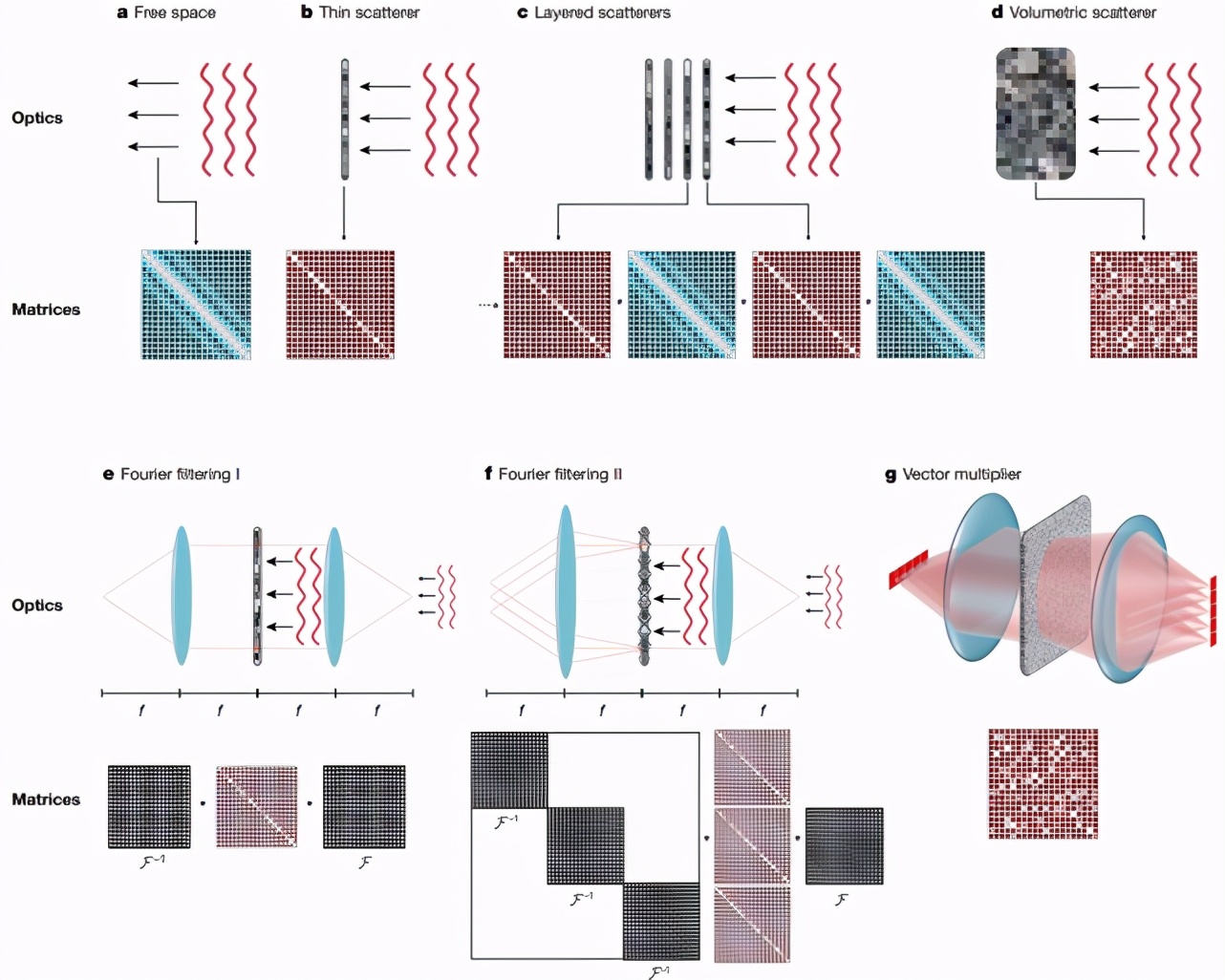
图 2:光波传播概况。如图所示,上面一行展示了波在自由空间和不同介质中的传播,下面一行是相应的线性矩阵运算。其中 a 是波穿过自由空间的情况,其在数学上被描述成波场与一个复值核的卷积。b-g 则使用了不同的介质,它们也因此有各自不同的矩阵。
使用深度计算光学和成像来执行推理
计算成像领域研究的是光学和图像处理的联合设计,这可用于增强计算式相机(computational camera)能力等应用。将相机解释成编码器 - 解码器系统会很有帮助。因此,我们可以从整体角度将相机设计问题看作是光学和成像处理的端到端优化问题。因此可以针对经由损失函数和训练数据集定义的特定任务对物理透镜和深度神经网络进行联合优化。(见下图 3)
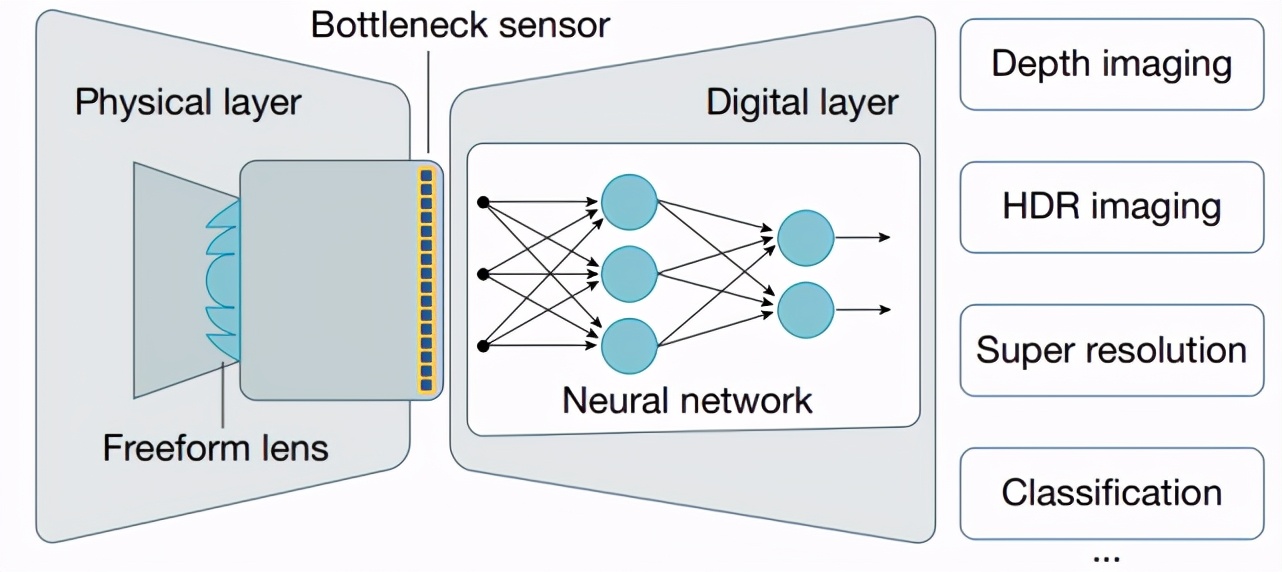
图 3:光学编码器 - 电子解码器系统示意图。其中传感器充当瓶颈,在角度、波长谱、曝光时间、相位和其它入射光指标上进行积分。自由曲面透镜或定制传感器电子设备能以离线方式针对特定任务进行优化,然后经过生产加工后用于从光学和电子方面记录图像编码。然后可以使用神经网络或其它可微分的图像处理算法来从观测结果提取所需的信息。这些编码器和解码器一起可共同组成一个混合式的光 - 电神经网络。
我们也可以将光学操作的原理解读为一种形式的计算,即与处理数据记录的电子平台一起工作的预处理器或协处理器。基于这一解读,我们可以让光学组件做尽可能多的工作,进而优化计算成像系统的延迟和功耗需求。
显微镜应用
光学显微镜也是深度学习方法已经取得重大影响的一个领域,其涵盖多种模态,包括相干成像以及明视野显微镜和荧光显微镜。解决显微图像重建和增强的反向问题已经是一项持续数十年的热门研究课题,之前方法的一大关键是建立成像系统的前向模型。基于深度学习的数据驱动方法是解决光学显微镜反向问题的另一条途径。
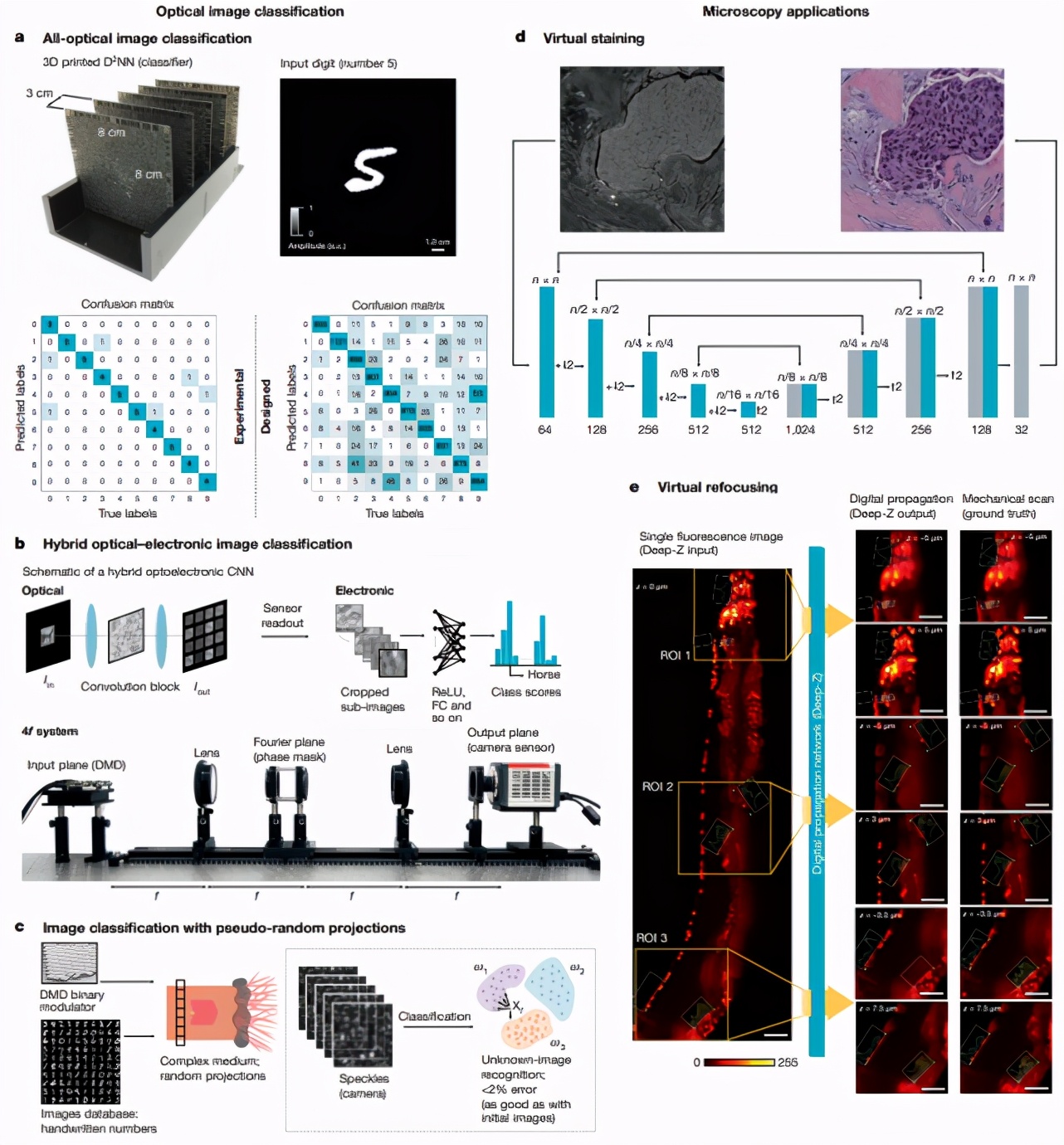
图 4:深度光学和光子学应用示例 I。a. 光学图像分类;b. 混合光电图像分类;c. 使用伪随机投影的图像分类;d. 虚拟染色;e. 虚拟重新聚焦。
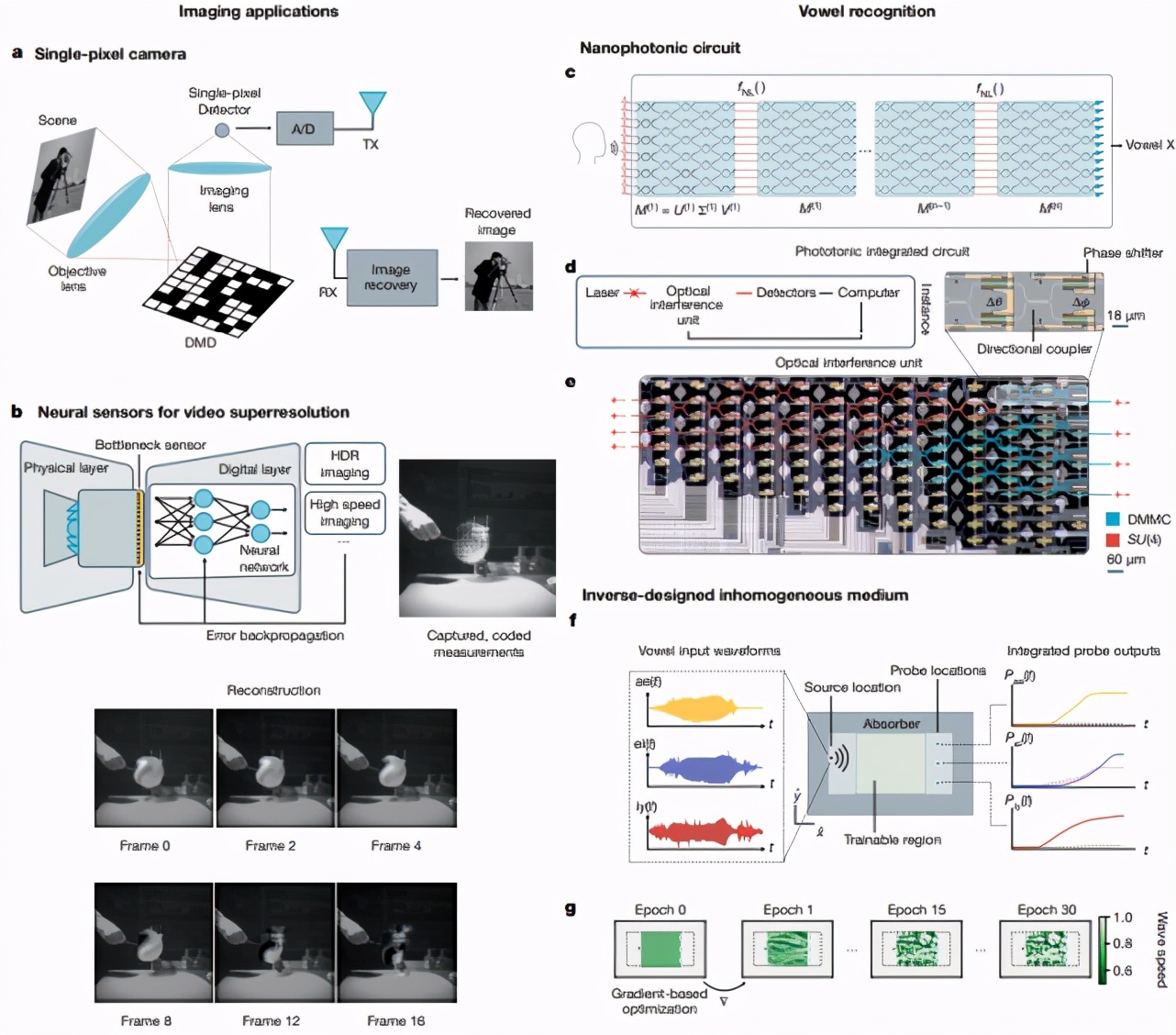
图 5:深度光学和光子学应用示例 I。a. 单像素相机;b. 用于视频超分辨率的神经传感器;c. 纳米光子回路;d. 光子集成电路;e. 光学干涉仪;f. 逆向设计的非均匀介质。
展望未来
文章认为,混合光 - 电计算系统是这一领域最有发展前景的方向。混合系统既具备光计算的带宽和速度优势,又具备电计算的灵活性,而且还能利用模拟和数字光学 / 光电 / 电子系统的高能效技术基础。混合光 - 电推理机器能将 AI 推理用于计算机视觉、机器人学、显微和其它视觉计算任务,进而实现光学计算机早该具有的变革性能力。