置换加密法是指重新排列文本中的字母。这种加密法与拼图游戏相似。在拼图游戏中,所有的图块都在这里,但它们最初的排列位置并不正确。置换加密法设计者的目标是设计一种方法,使您在知道密钥的情况下,能将图块很容易地正确排序。如果没有这个密钥,就很难正确地拼接图块。密码分析者(攻击者)的目标是在没有密钥的情况下重组拼图,或从拼图的特征中发现密钥。设计置换加密法的目标是让攻击者的这两个目标都很难实现。
置换加密法的分类结构如图1所示。
图1 置换加密法的分类结构
1、Skytale加密法
斯巴达人是最早将置换加密法用于军事消息传递的人之一。他们发明了一种被称为Skytale的工具(见图2)。Skytale就是一种加密用的、具有一定粗细的棍棒或权杖。斯巴达人把重要的信息写在缠绕于Skytale上的皮革或羊皮纸上之后,再把皮革或羊皮纸解下来,这样就能有效地打乱字母顺序。只有把皮革或羊皮纸再一点点卷回与原来加密的Skytale同样粗细的棍棒上后,文字信息才能逐圈并列呈现在棍棒的表面,进而还原出它本来的意思。
图2 Skytale示例
置换加密法使用的密钥通常是一些几何图形,它决定了重新排列字母的方式。例如,Skytale加密法的密钥是Skytale杆,就是用它来打乱字母顺序的。明文字母按一个方向填写(例如,Skytale加密法是从上到下填写),再从另一个方向读取(例如,Skytale加密法是将皮革或羊皮纸卷起来后从左到右读取)。
2、栅栏密码加密法
栅栏密码(Rail-fence)加密法(见图3)不是按从上到下的方式填写明文和读取密文的,而是使用了对角线方式。在这种加密法中,明文是按“Z”字形的方式填写在矩形的对角线上的,然后按行读取以生成密文。例如,如果矩形的高为3,长为11,那么明文“this is a test”在该矩形中的填写如图3所示,此时,按行读取所生成的密文就是“tiehsstsiat”。
图3 Rail-fence加密法示例
同样的过程可以应用于其他几何图形。例如,在一个固定大小的矩形中,可以将明文填写成一个三角形,然后,按列读取生成密文。图4是将明文“You mustdo that now”填写在一个7×4的矩形中,此时,按列读取生成的密文是“tuhosayuttmdnoow”。
图4 三角加密法示例
3、平移置换加密法
置换加密法的一种简单实现形式是平移置换加密法,这很像洗一副纸牌。在平移置换加密法中,将密文分成了固定长度的块。通常,块越大越不容易破译。设块大小为s,置换函数f用于从1到s中选取一个整数,每个块中的字母根据f重新排列。这种加密法的密钥就是(s,f)对应的具体数值。例如,设s为4,f给定为(2,4,1,3)。这意味着第1个字符移到位置2,第2个字符移到位置4,第3个字符移到位置1,第4个字符移到位置3。
例如,利用这种置换加密法将明文“The only limit to our realization of tomorrow will be our doubts of today”加密。首先,设置密钥(s,f),如将s设为7,则明文将被分成块,每块包含7个字母,不足的用空字符填满。然后,根据给定的函数f=(4,2,3,5,7,6,1)将每个块重新排列,生成对应的密文,如图5所示。
图5 明文和密文示例
可以用密文攻击法和已知明文攻击法来破解平移置换加密法。密文攻击法通过查看密文块,查找出可能生成可读单词的排列方式。一旦发现了某个块的置换方式,就可以将其应用到03密文的所有块中。如果密码分析员熟悉通过颠倒字母顺序来构成单词,那么破解平移置换加密法就是一个简单的工作了。已知明文攻击法就更简单,知道了明文中可能包含的一个单词后,攻击法可分3个步骤对密文进行破解:
1)找出包含组成已知单词的各字母的块;
2)通过比较已知单词与密文块,确定置换方式;
3)在密文的其他块上测试上面得出的置换方式。
4、列置换加密法
列置换加密法是将明文按行填写在一个矩形中,而密文则是以预定的顺序按列读取生成的。例如,如果矩形是4列5行,那么短语“encryption algorithms”可以如图6所示写入矩形中。
图6 列置换矩形示例
按一定的顺序读取列以生成密文。对于这个示例,如果读取顺序是4、1、2、3,那么密文就是“riliseyogtnpnohctarm”。这种加密法要求填满矩形,因此,如果明文的字母不够,可以添加“x”或“q”甚至空字符。
这种加密法的密钥是列数和读取列的顺序。如果列数很多,则记起来可能会比较闲难,因此可以将它表示成一个关键词,以方便记忆。该关键词的长度等于列数,而其字母顺序决定读取列的顺序。
例如,关键词“general”有7个字母,意味着矩形有7列。若按字母在字母表中的顺序进行排序,则由关键词general可知读取列顺序为4、2、6、3、7、1、5。图7给出了一个列置换矩形加密示例。
图7 列置换矩形加密示例
对于列置换矩形加密的破译,强力攻击法就是尝试所有可能的列和行,代价较高且收效甚微。正确的方法是将这个问题进行分解,可以通过3步来破解列置换加密法。首先,尝试确定换位矩形的可能大小(多少行和多少列)。然后,尝试在这些可能的矩形中找出正确的。最后,知道正确的矩形之后,尝试重新排列矩形列,以便还原消息。
(1)确定列的可能大小
这是强力攻击法的第一步,也是最简单的工作。因为该加密法完全是列换行,所以密文字符的数目必须是行数乘以列数的积。例如,假设截获的消息有153个字符,153可以分解为3×51、51×3、17×9或9×17。假设这个消息是在一个矩形中换位的,那么这4个积肯定定义了其大小,也就是说,这个矩形有3行51列、51行3列、17行9列或9行17列。没有其他矩形可以完全填满这153个字符了。由于3×51或51×3的列和行相差较大,因此不太可能是加密用的矩形。最有可能的是17×9或9×17。因此,下一步就是找出这两者之间哪个是正确的。
(2)确定正确的矩形
这个过程是基于一个事实,即矩形的每行表示的都是标准英语的一行。明文的所有字母仍出现在密文中,它们只是错位了而已。因此可以依靠英语的常见属性来检测密文最可能的排列方式。例如,英语中的每句话包含大约40%的元音字母,如果某个矩形的元音字母分布满足每行40%的标准,那么这种推测很可能就是正确的。
9×17的矩形有9行,因此每行应有大约3.6个元音字母。将密文填入这个矩形中,并计算每行的元音字母数目。计算出实际的元音字母数与期望的元音字母数之差的绝对值,并将这些差值相加,即可生成该矩形的得分。最佳得分对应的差值总和最小。
(3)还原列的顺序
破解列置换加密法的最后一步是找出列的正确顺序。这是通过颠倒字母顺序来构成词的过程,需要充分利用字母的一些特征,如引导字符、连字集加权等。
根据列置换加密法的加密原理还衍生出一些变种,如铁轨法。铁轨法要求明文的长度必须是4的倍数,若不符合要求,则在明文最后加上一些字母以符合加密的条件。将明文以从上到下的顺序分两行逐行写出。依序由左而右再由上而下地写出字母即为密文(在写明文时也可以写成3行或4行等,写法不同,解法也相应不同)。例如,明文“STRIKE WHILE THE IRON IS HOT”,首先,该明文不满足条件,故在尾端加上字母“E”,使明文的长度变成4的倍数。然后,将明文以从上到下的顺序逐行写出,如下所示:
S R K W I E H I O I H T
T I E H L T E R N S O E
依序由左而右再由上而下地写出字母,即为密文:SRKWIEHIOIHTTIEHLTERNSOE。
铁轨法的解密过程也非常简单,如上例中将密文每4个字母一组,组间用空格隔开,即可得:
SRKW IEHI OIHT TIEH LTER NSOE
因为知道加密的顺序,所以接收方可将密文用一直线从中间分为两个部分,如下所示:
SRKW IEHI OIHT | TIEH LTER NSOE
然后左右两半依序轮流读出字母便可还原明文。
路游法可以说是铁轨法的一种推广。此方法也必须将明文的长度调整为4的倍数,之后再将调整过的明文依序由左而右再由上而下的顺序(此顺序称为排列顺序)填入方格矩形中。依照某一事先规定的路径(称为游走路径)来游走矩形并输出所经过的字母,即为密文。路游法的安全性主要取决于排列顺序与游走路径的设计,但必须注意的是,排列顺序与游走路径绝不可相同,否则便无法加密。
依前例明文为:STRIKE WHILE THE IRON IS HOT,将此明文放入矩形且若以图8所示的路径游走,则可得到密文:ETNETOEKILROHIIRTHESIHWS。
图8 游走路径示意
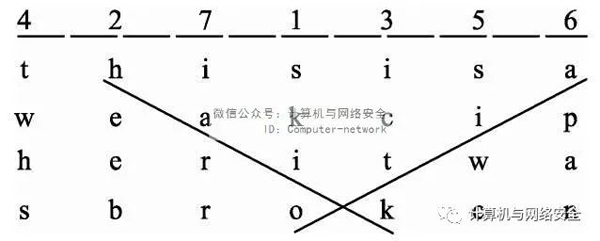
法国人在第一次世界大战时期使用的是一种换位算法——中断列换位法。在这种加密法中,先读取某些预定的对角线字母,然后再读取各列,读取各列时忽略已读的字母。例如,在图9所示的模式中,首先读取对角线的字母,然后再读取各列,结果密文为“haik aito sk eeb ic twhs swc pan irr”。
图9 中断列换位法字母读取模式示意
双重列换位加密法,正如其名称所暗示的那样,会先用列换位法将明文加密,然后再用列换位法将第一次换位加密的密文加密。这两次换位所使用的关键词可以相同。经两次换位后,明文字母的位置会被完全打乱。
5、双重换位加密法
第一次世界大战时期,德国使用过一种著名而复杂的双重换位加密法。一个关键词短语(使用字母顺序方法)会被转换成一个数字序列。例如,关键词短语为“next time”,那么其数字短语对应如下:
n e x t t i m e
5 1 8 6 7 3 4 2
首先,将明文(如“bob I need to see you at the office now alice”)“逐行”填写在这个数字序列的下面,如下所示:
5 1 8 6 7 3 4 2
b o b i n e e d
t o s e e y o u
a t t h e o f f
i c e n o w a l
i c e
然后,按列的顺序将这些列下的字母“逐行”填写在相同的数字序列下面,如下所示:
5 1 8 6 7 3 4 2
o o t c c d u f
l e y o w e o f
a b t a i i i e
h n n e e o b s
t e e
最后,按列的顺序读取这些字母,就会生成密文“oebne ffesd eiouo ibola htcoa ecwie tytne”。
利用该加密法通常会生成没有完全填充满的列换位,这会使密码分析员破解密码更加困难。在第一次世界大战爆发之前,法国已经开始准备加密工作了。他们最初的成就是开发了一个功能强大的无线通信分析系统。法国人的努力得到了回报,他们可以破解和阅读德国用双重列换位加密法加密的很多消息。
6、旋转方格加密法
在第一次世界大战期间,德国军队使用的加密法从换位加密法改成了替换加密法。到了1916年,他们又改回了换位加密法。这一次他们采用了旋转方格。旋转方格首次出现在兴登堡(Hindenburg)于1796年写的一本书中,并很快就流行了起来。旋转方格加密法在18世纪末被使用得很频繁,后来又在第一次世界大战时期被德国使用。图10是一个典型的旋转方格和一些样本明文(this is an example of a turning grille for us)。如果将旋转方格放在明文上面,那么显示的第一个密文集就如图11~图14所示。这些密文按行的顺序可写为“hinxetios”,最终的密文为“hinxetios iampouile tseanrlfu salfrnggr”。
图10 典型旋转方格示例与明文
图11 未旋转时的旋转方格示例与明文
图12 旋转方格第1次旋转与明文
图13 旋转方格第2次旋转与明文
图14 旋转方格第3次旋转与明文
旋转方格的解密过程很简单,只须每次顺时针旋转90°时将对应的密文填入空白格,即可恢复明文。
总之,随着密码分析技术和计算能力的迅猛发展,明文和密文在变换过程中仅做位置上的移动是远远不够的,还必须要有码值上的变化。原始的换位密码算法在抗攻击方面的最大弱点是它不能抵抗差分攻击。若要抵抗差分攻击,明密文间必须要有很好的混合与扩散性质。因此,实用的换位密码算法必须借助某种代替变换作为辅助手段,依此加强明密文变换间的非线性,以便抵抗一些现代密码攻击方法。
由于换位密码算法有两个优点:一是换位密码算法有广阔的密钥空间,二是换位变换是一种极易实现的快速变换,因此它还不会被人们遗忘。尽管代替作业密码相比换位密码已经极其逊色,但其仍然具有顽强的生命力,当然这种生命力的客观存在依赖于未来密码设计者的精心呵护。