本文转载自公众号“读芯术”(ID:AI_Discovery)。
本文将介绍强化学习算法的分类法,从多种不同角度学习几种分类法。话不多说,大家深呼吸,一起来学习RL算法的分类吧!
无模型(Model-Free)VS基于模型(Model-Based)
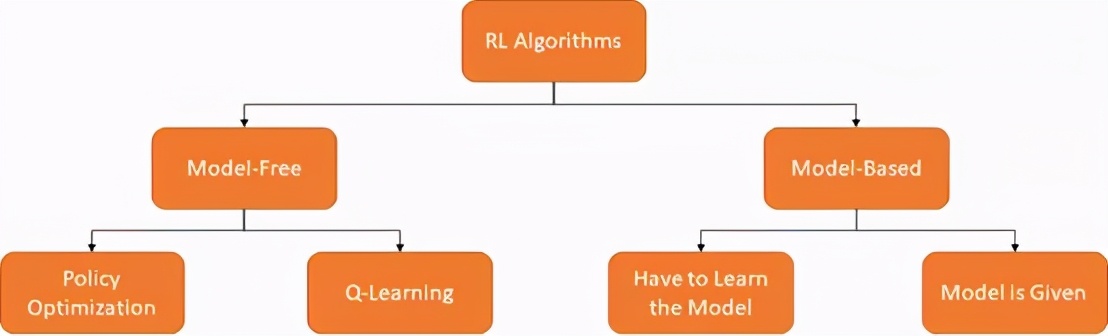
无模型VS模型分类法 [图源:作者,OpenAISpinning Up再创作]
RL算法的一种分类方法是询问代理是否能访问环境模型。换言之,询问环境会否响应代理的行为。基于这个观点有两个RL算法的分支:无模型和基于模型。
- 模型RL算法根据环境的学习模型来选择最佳策略。
- 无模型RL算法通过代理反复测试选择最佳策略。
两种算法都各有优缺点,如下表所示:

基于价值VS 基于政策
RL算法的另一种分类方法是考虑算法优化了价值函数还是策略。在深入了解之前,我们先了解策略和价值功能。
(1) 策略
策略π是从状态s到动作a的映射,其中π(a | s)是在状态s时采取动作a的概率。策略可以是确定的,也可以是随机的。
假设我们在玩剪刀石头布这个非常简单的游戏,两个人通过同时执行三个动作(石头/剪刀/布)中的一个来比输赢。规则很简单:
- 剪刀克布
- 石头克剪刀
- 布克石头
把策略看作是迭代的剪刀石头布
- 确定性策略容易被利用-如果我意识到你出“石头”较多,那么我可以利用这一点,获得更大赢面。
- 统一的随机策略(uniform random policy)最佳—如果你的选择完全随机,那我就不知道该采取什么行动才能取胜。
(2) 价值函数
价值函数是根据对未来回报(返回值)的预测来衡量状态良好程度的函数。返回值(Gt)基本等于“折扣”回报的总和(自t时起)。
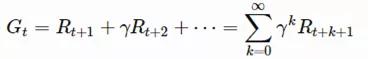
γ ∈ [0,1]是折扣因数。折扣因数旨在抵扣未来的回报,有以下几个原因:
- 方便数学计算
- 打破状态变化图中的无限循环
- 未来回报的高度不确定性(比如股价变化)
- 未来回报不能立时受益(比如人们更愿意当下享乐而非十年后)
了解了返回值的概念后,接下来定义价值函数的数学形式吧!
价值函数的数学形式有二:
状态-动作价值函数(Q值)是t时状态动作组合下的期望返回值:
Q值和价值函数之间的区别是动作优势函数(通常称为A值):
现在知道了什么是价值函数和动作-状态价值函数。接下来学习有关RL算法另一个分支的更多信息,该分支主要关注算法优化的组件。
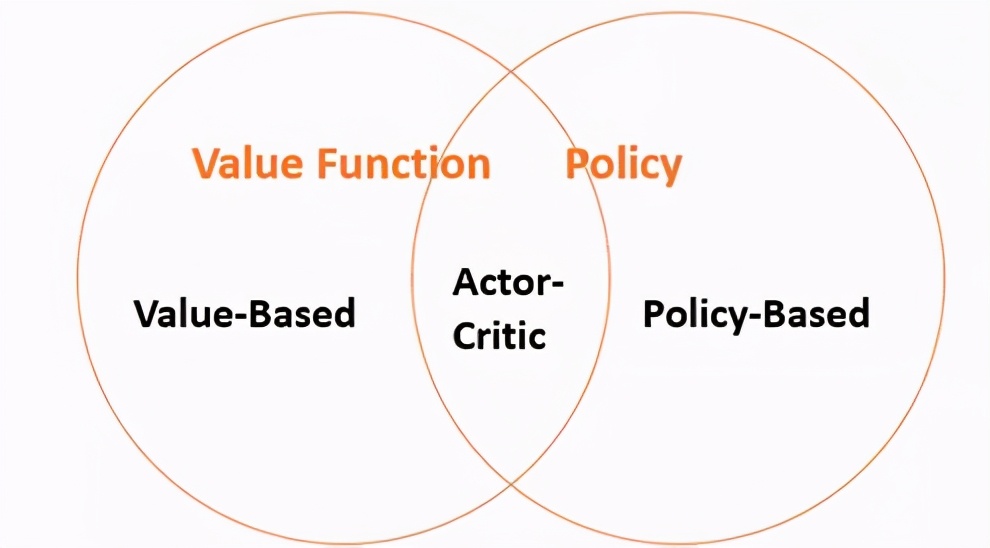
价值算法与策略算法[图源:作者,David Silver RL课程再创作]
- 价值RL旨在学习价值/行动-价值函数,以生成最佳策略(即,隐式生成最佳策略);
- 策略RL旨在使用参数化函数直接学习策略。
- Actor-Critic RL旨在学习价值函数和策略。
下表列出了价值和策略算法的优缺点。

- 价值算法必须选择使动作-状态价值函数最大的动作,如果动作空间非常高维或连续,成本就会很高,而策略算法是通过直接调整策略的参数来运行的,不需要进行最大化计算。
- 如果操作不当 (收敛性质差/不稳定),价值算法会出现一系列问题,而策略算法更稳定,收敛性质更好,因为它们只对策略梯度进行很少的增量更改。
- 策略算法既可以学习确定性策略,也可以学习随机策略,而价值算法只能学习确定性策略。
- 与价值算法相比,原本的策略算法速度更慢,方差更大。价值算法试图选择使动作-状态价值函数最大化的动作,这将优化策略 (运算更快、方差更小),策略算法只需几步,并且更新顺畅、稳定,但同时效率较低,有时会导致方差变大。
- 策略算法通常收敛于局部最优而不是全局最优。
策略和非策略算法
还有一种RL算法分类方法是基于策略来源分类。
可以说策略算法是“边做边学”。也就是说该算法试着从π采样的经验中了解策略π。而非策略算法是通过“监视”的方式来工作。换句话说,该算法试图从μ采样的经验中了解策略π。例如,机器人通过观察人类的行为来学习如何操作。