本文转载自微信公众号「bigsai」,作者bigsai 。转载本文请联系bigsai公众号。
前言
分治算法(divide and conquer)是五大常用算法(分治算法、动态规划算法、贪心算法、回溯法、分治界限法)之一,很多人在平时学习中可能只是知道分治算法,但是可能并没有系统的学习分治算法,本篇就带你较为全面的去认识和了解分治算法。
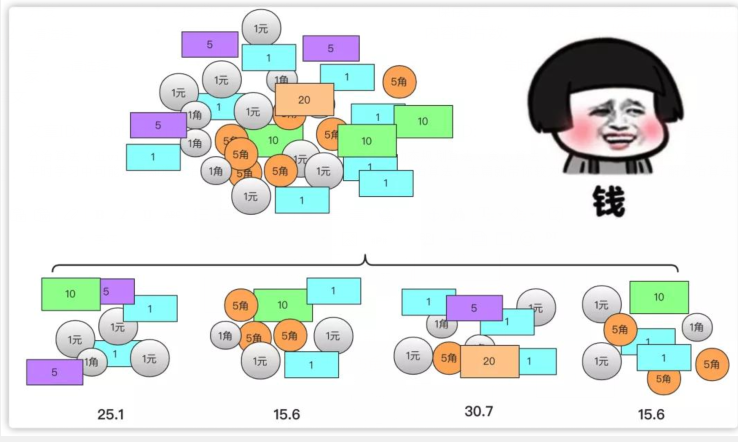
在学习分治算法之前,问你一个问题,相信大家小时候都有存钱罐的经历,父母亲人如果给钱都会往自己的宝藏中存钱,我们每隔一段时间都会清点清点钱。但是一堆钱让你处理起来你可能觉得很复杂,因为数据相对于大脑有点庞大了,并且很容易算错,你可能会将它先分成几个小份算,然后再叠加起来计算总和就获得这堆钱的总数了
当然如果你觉得各个部分钱数量还是太大,你依然可以进行划分然后合并,我们之所以这么多是因为:
计算每个小堆钱的方式和计算最大堆钱的方式是相同的(区别在于体量上)
然后大堆钱总和其实就是小堆钱结果之和。这样其实就有一种分治的思想。
当然这些钱都是想出来的……
分治算法介绍
分治算法是用了分治思想的一种算法,什么是分治?
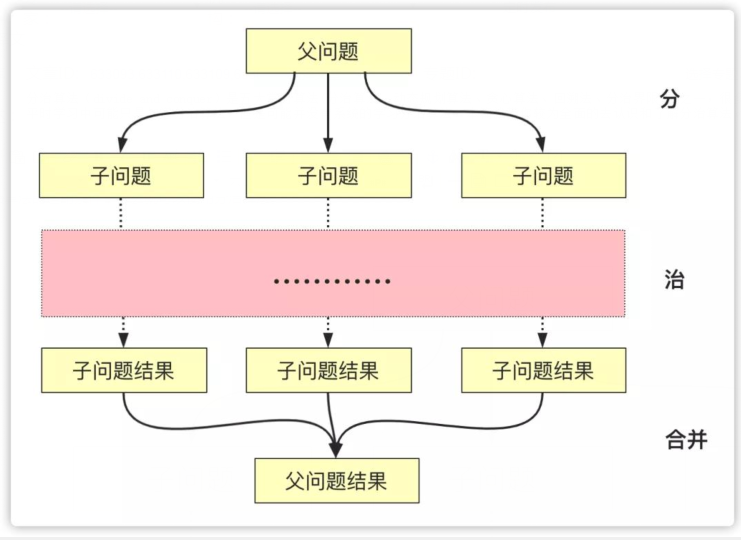
分治,字面上的解释是“分而治之”,就是把一个复杂的问题分成两个或更多的相同或相似的子问题,再把子问题分成更小的子问题……直到最后子问题可以简单的直接求解,原问题的解即子问题的解的合并。在计算机科学中,分治法就是运用分治思想的一种很重要的算法。分治法是很多高效算法的基础,如排序算法(快速排序,归并排序),傅立叶变换(快速傅立叶变换)等等。
将父问题分解为子问题同等方式求解,这和递归的概念很吻合,所以在分治算法通常以递归的方式实现(当然也有非递归的实现方式)。分治算法的描述从字面上也很容易理解,分、治其实还有个合并的过程:
- 分(Divide):递归解决较小的问题(到终止层或者可以解决的时候停下)
- 治(Conquer):递归求解,如果问题够小直接求解。
- 合并(Combine):将子问题的解构建父类问题
一般分治算法在正文中分解为两个及以上的递归调用,并且子类问题一般是不相交的(互不影响)。当求解一个问题规模很大很难直接求解,但是规模较小的时候问题很容易求解并且这个问题并且问题满足分治算法的适用条件,那么就可以使用分治算法。
那么采用分治算法解决的问题需要 满足那些条件(特征) 呢?
1 . 原问题规模通常比较大,不易直接解决,但问题缩小到一定程度就能较容易的解决。
2 . 问题可以分解为若干规模较小、求解方式相同(似)的子问题。且子问题之间求解是独立的互不影响。
3 . 合并问题分解的子问题可以得到问题的解。
你可能会疑惑分治算法和递归有什么关系?其实分治重要的是一种思想,注重的是问题分、治、合并的过程。而递归是一种方式(工具),这种方式通过方法自己调用自己形成一个来回的过程,而分治可能就是利用了多次这样的来回过程。
分治算法经典问题
对于分治算法的经典问题,重要的是其思想,因为我们大部分借助递归去实现,所以在代码实现上大部分都是很简单,而本篇也重在讲述思想。
分治算法的经典问题,个人将它分成两大类:子问题完全独立和子问题不完全独立。
1 . 子问题完全独立就是原问题的答案可完全由子问题的结果推出。
2 . 子问题不完全独立,有些区间类的问题或者跨区间问题使用分治可能结果跨区间,在考虑问题的时候需要仔细借鉴下。
二分搜索
二分搜索是分治的一个实例,只不过二分搜索有着自己的特殊性
- 序列有序
- 结果为一个值
正常二分将一个完整的区间分成两个区间,两个区间本应单独找值然后确认结果,但是通过有序的区间可以直接确定结果在哪个区间,所以分的两个区间只需要计算其中一个区间,然后继续进行一直到结束。实现方式有递归和非递归,但是非递归用的更多一些:
- public int searchInsert(int[] nums, int target) {
- if(nums[0]>=target)return 0;//剪枝
- if(nums[nums.length-1]==target)return nums.length-1;//剪枝
- if(nums[nums.length-1]<target)return nums.length;
- int left=0,right=nums.length-1;
- while (left<right) {
- int mid=(left+right)/2;
- if(nums[mid]==target)
- return mid;
- else if (nums[mid]>target) {
- right=mid;
- }
- else {
- left=mid+1;
- }
- }
- return left;
- }
快速排序
快排也是分治的一个实例,快排每一趟会选定一个数,将比这个数小的放左面,比这个数大的放右面,然后递归分治求解两个子区间,当然快排因为在分的时候就做了很多工作,当全部分到最底层的时候这个序列的值就是排序完的值。这是一种分而治之的体现。
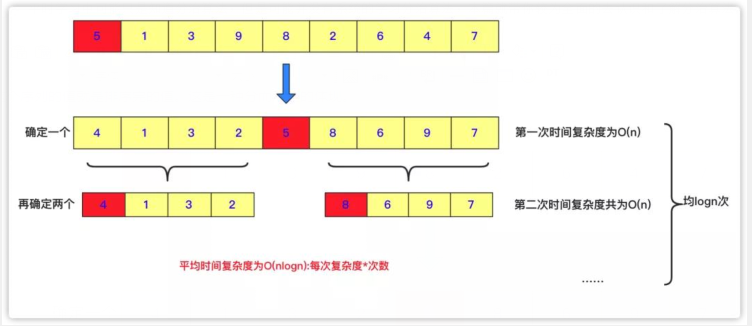
- public void quicksort(int [] a,int left,int right)
- {
- int low=left;
- int high=right;
- //下面两句的顺序一定不能混,否则会产生数组越界!!!very important!!!
- if(low>high)//作为判断是否截止条件
- return;
- int k=a[low];//额外空间k,取最左侧的一个作为衡量,最后要求左侧都比它小,右侧都比它大。
- while(low<high)//这一轮要求把左侧小于a[low],右侧大于a[low]。
- {
- while(low<high&&a[high]>=k)//右侧找到第一个小于k的停止
- {
- high--;
- }
- //这样就找到第一个比它小的了
- a[low]=a[high];//放到low位置
- while(low<high&&a[low]<=k)//在low往右找到第一个大于k的,放到右侧a[high]位置
- {
- low++;
- }
- a[high]=a[low];
- }
- a[low]=k;//赋值然后左右递归分治求之
- quicksort(a, left, low-1);
- quicksort(a, low+1, right);
- }
归并排序(逆序数)
快排在分的时候做了很多工作,而归并就是相反,归并在分的时候按照数量均匀分,而合并时候已经是两两有序的进行合并的,因为两个有序序列O(n)级别的复杂度即可得到需要的结果。而逆序数在归并排序基础上变形同样也是分治思想求解。
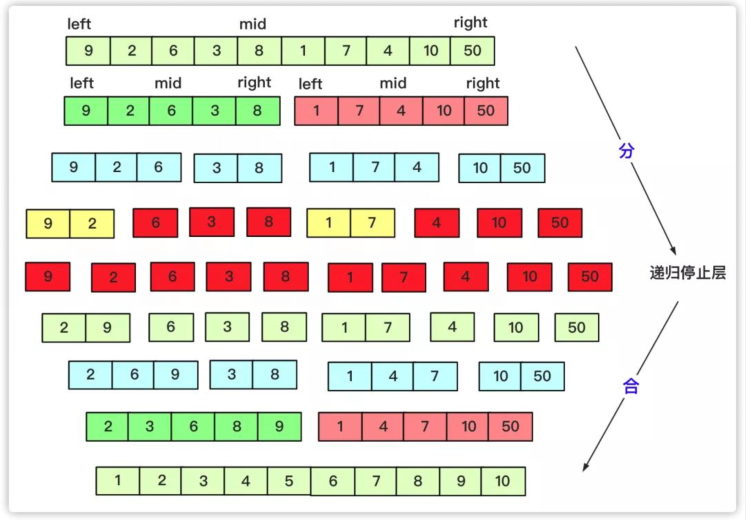
- private static void mergesort(int[] array, int left, int right) {
- int mid=(left+right)/2;
- if(left<right)
- {
- mergesort(array, left, mid);
- mergesort(array, mid+1, right);
- merge(array, left,mid, right);
- }
- }
- private static void merge(int[] array, int l, int mid, int r) {
- int lindex=l;int rindex=mid+1;
- int team[]=new int[r-l+1];
- int teamindex=0;
- while (lindex<=mid&&rindex<=r) {//先左右比较合并
- if(array[lindex]<=array[rindex])
- {
- team[teamindex++]=array[lindex++];
- }
- else {
- team[teamindex++]=array[rindex++];
- }
- }
- while(lindex<=mid)//当一个越界后剩余按序列添加即可
- {
- team[teamindex++]=array[lindex++];
- }
- while(rindex<=r)
- {
- team[teamindex++]=array[rindex++];
- }
- for(int i=0;i<teamindex;i++)
- {
- array[l+i]=team[i];
- }
- }
最大子序列和
最大子序列和的问题我们可以使用动态规划的解法,但是也可以使用分治算法来解决问题,但是最大子序列和在合并的时候并不是简单的合并,因为子序列和涉及到一个长度的问题,所以正确结果不一定全在最左侧或者最右侧,而可能出现结果的区域为:
- 完全在中间的左侧
- 完全在中间的右侧
- 包含中间左右两个节点的一个序列
用一张图可以表示为:
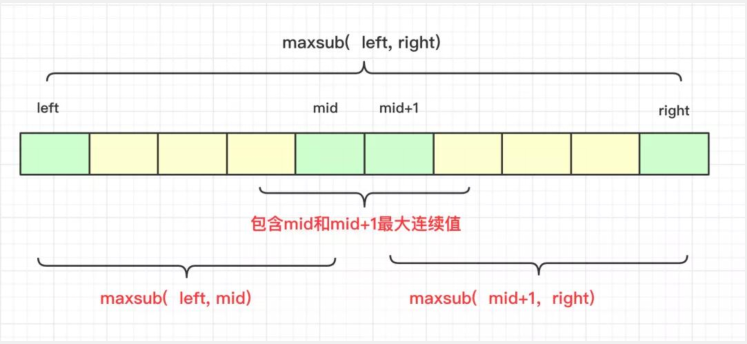
所以在具体考虑的时候需要将无法递归得到结果的中间那个最大值串的结果也算出来参与左侧、右侧值得比较。
力扣53. 最大子序和在实现的代码为:
- ublic int maxSubArray(int[] nums) {
- int max=maxsub(nums,0,nums.length-1);
- return max;
- }
- int maxsub(int nums[],int left,int right)
- {
- if(left==right)
- return nums[left];
- int mid=(left+right)/2;
- int leftmax=maxsub(nums,left,mid);//左侧最大
- int rightmax=maxsub(nums,mid+1,right);//右侧最大
- int midleft=nums[mid];//中间往左
- int midright=nums[mid+1];//中间往右
- int team=0;
- for(int i=mid;i>=left;i--)
- {
- team+=nums[i];
- if(team>midleft)
- midleft=team;
- }
- team=0;
- for(int i=mid+1;i<=right;i++)
- {
- team+=nums[i];
- if(team>midright)
- midright=team;
- }
- int max=midleft+midright;//中间的最大值
- if(max<leftmax)
- max=leftmax;
- if(max<rightmax)
- max=rightmax;
- return max;
- }
最近点对
最近点对是一个分治非常成功的运用之一。在二维坐标轴上有若干个点坐标,让你求出最近的两个点的距离,如果让你直接求那么枚举暴力是个非常非常大的计算量,我们通常采用分治的方法来优化这种问题。
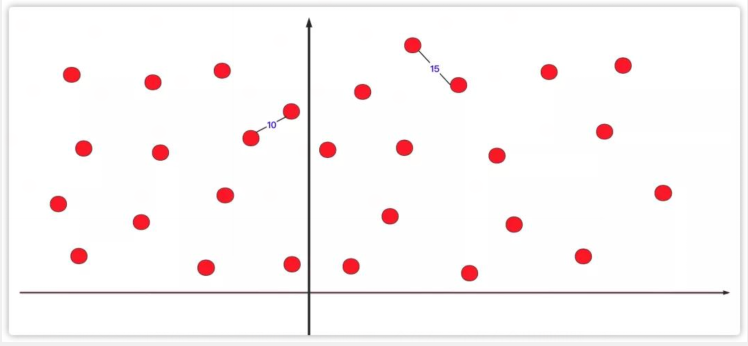
如果直接分成两部分分治计算你肯定会发现如果最短的如果一个在左一个在右会出现问题。我们可以优化一下。
在具体的优化方案上,按照x或者y的维度进行考虑,将数据分成两个区域,先分别计算(按照同方法)左右区域内最短的点对。然后根据这个两个中较短的距离向左和向右覆盖,计算被覆盖的左右点之间的距离,找到最小那个距离与当前最短距离比较即可。
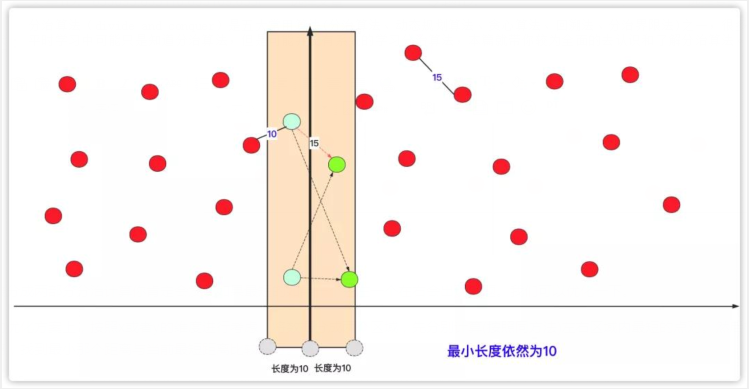
这样你就可以发现就这个一次的操作(不考虑的情况),左侧红点就避免和右侧大部分红点进行距离计算(O(n2)的时间复杂度)。事实上,在进行左右区间内部计算的时候,它其实也这样递归的进行很多次分治计算。如图所示:
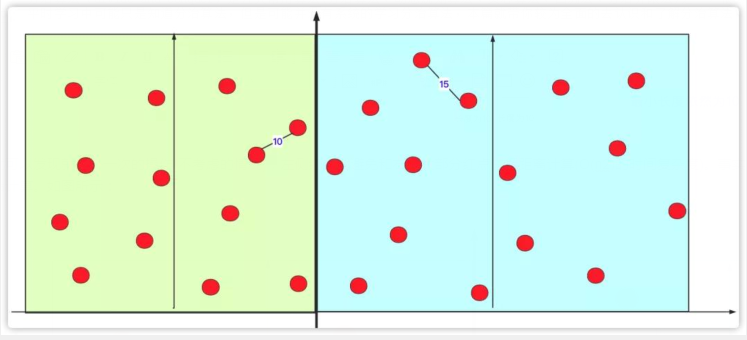
这样下去就可以节省很多次的计算量。
但是这种分治会存在一种问题就是二维坐标可能点都聚集某个方法某条轴那么可能效果并不明显(点都在x=2附近对x分割作用就不大),需要注意一下。
杭电1007推荐给大家,ac的代码为:
- import java.io.BufferedReader;
- import java.io.IOException;
- import java.io.InputStreamReader;
- import java.io.OutputStreamWriter;
- import java.io.PrintWriter;
- import java.io.StreamTokenizer;
- import java.util.ArrayList;
- import java.util.Arrays;
- import java.util.Comparator;
- import java.util.List;
- public class Main {
- static int n;
- public static void main(String[] args) throws IOException {
- StreamTokenizer in=new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
- PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
- //List<node>list=new ArrayList();
- while(in.nextToken()!=StreamTokenizer.TT_EOF)
- {
- n=(int)in.nval;if(n==0) {break;}
- node no[]=new node[n];
- for(int i=0;i<n;i++)
- {
- in.nextToken();double x=in.nval;
- in.nextToken();double y=in.nval;
- // list.add(new node(x,y));
- no[i]=new node(x,y);
- }
- Arrays.sort(no, com);
- double min= search(no,0,n-1);
- out.println(String.format("%.2f", Math.sqrt(min)/2));out.flush();
- }
- }
- private static double search(node[] no, int left,int right) {
- int mid=(right+left)/2;
- double minleng=0;
- if(left==right) {return Double.MAX_VALUE;}
- else if(left+1==right) {minleng= (no[left].x-no[right].x)*(no[left].x-no[right].x)+(no[left].y-no[right].y)*(no[left].y-no[right].y);}
- else minleng= min(search(no,left,mid),search(no,mid,right));
- int ll=mid;int rr=mid+1;
- while(no[mid].y-no[ll].y<=Math.sqrt(minleng)/2&&ll-1>=left) {ll--;}
- while(no[rr].y-no[mid].y<=Math.sqrt(minleng)/2&&rr+1<=right) {rr++;}
- for(int i=ll;i<rr;i++)
- {
- for(int j=i+1;j<rr+1;j++)
- {
- double team=0;
- if(Math.abs((no[i].x-no[j].x)*(no[i].x-no[j].x))>minleng) {continue;}
- else
- {
- team=(no[i].x-no[j].x)*(no[i].x-no[j].x)+(no[i].y-no[j].y)*(no[i].y-no[j].y);
- if(team<minleng)minleng=team;
- }
- }
- }
- return minleng;
- }
- private static double min(double a, double b) {
- // TODO 自动生成的方法存根
- return a<b?a:b;
- }
- static Comparator<node>com=new Comparator<node>() {
- @Override
- public int compare(node a1, node a2) {
- // TODO 自动生成的方法存根
- return a1.y-a2.y>0?1:-1;
- }};
- static class node
- {
- double x;
- double y;
- public node(double x,double y)
- {
- this.x=x;
- this.y=y;
- }
- }
- }
结语
到这里,分治算法就讲这么多了,因为分治算法重要在于理解其思想,还有一些典型的分治算法解决的问题,例如大整数乘法、Strassen矩阵乘法、棋盘覆盖、线性时间选择、循环赛日程表、汉诺塔等问题你可以自己研究其分治的思想和原理。
原文链接:https://mp.weixin.qq.com/s/jHiBOjfyMvuvGzSecsdNPw