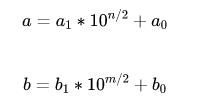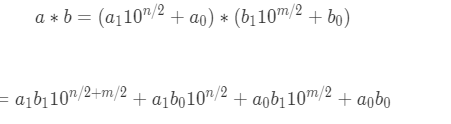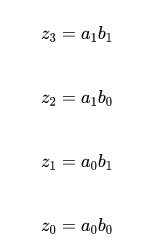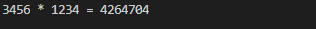看了就会的大整数乘法运算与分治算法-大整数运算

[[352004]]

在数据加密处理中有很多复杂的加密算法，这些加密算法往往会用到很多超大的整数运算。不过，程序设计语言对数据的大小会有一定的限制，数据太大就会出现数据溢出的情况，这是无法进行大整型数据运算的。本文将和大家一起学习如何实现大整数的数据运算，本文代码我们使用C++实现。

普通乘数运算

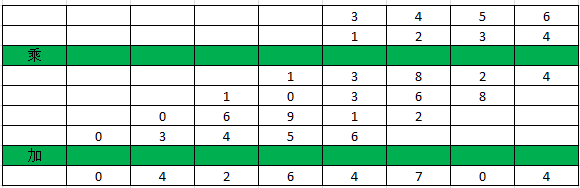
对于乘数运算有一种比较简单较为容易理解的方法，我们可以利用小学时期学的列竖式的计算方法进行乘法运算。

列竖式乘法运算

参考上图中的列竖式计算方法，我们进行代码实现。

#include <iostream> 
#include <string> 
#include <stdlib.h> 
#include <vector> 
#include <cstring> 
#include <algorithm> 
 
std::string multiply(std::string a, std::string b) 
{ 
    std::string result = ""; 
    int row = b.size(); 
    int col = a.size() + 1; 
    int tmp[row][col]; 
    memset(tmp,0, sizeof(int)*row*col); 
     
    reverse(a.begin(),a.end()); 
    reverse(b.begin(),b.end()); 
     
    for(int i = 0; i < b.size(); i++) 
    { 
        for(int j = 0; j < a.size(); j++) 
        { 
            std::string bit_a = std::string(1, a.at(j)); 
            std::string bit_b = std::string(1, b.at(i)); 
             
            tmp[i][j] += std::stoi(bit_a) * std::stoi(bit_b); 
         
            tmp[i][j+1] = tmp[i][j] / 10; 
            tmp[i][j] %= 10; 
 
        } 
 
    } 
 
    int N =  a.size() + b.size(); 
    int sum[N]; 
    memset(sum, 0, sizeof(int)*N); 
     
    for(int n = 0; n < N; n++) 
    { 
        int i = 0; 
        int j = n; 
         
        while (i <= n && j >= 0 ) 
        { 
            if(i < row && j < col) 
            { 
                sum[n] += tmp[i][j]; 
            } 
             
            i++; 
            j--; 
        } 
 
        if( n+1 < N ) 
        { 
            sum[n+1] = sum[n] / 10; 
            sum[n] %= 10; 
        } 
 
    } 
 
    bool zeroStartFlag = true; 
    for (int i = N-1; i >= 0; i--) 
    { 
        if(sum[i]==0 && zeroStartFlag) 
        { 
            continue; 
        } 
         
        zeroStartFlag = false; 
        result.append(std::to_string(sum[i])); 
    } 
     
    return result; 
} 
 
 
int main() 
{ 
    std::string a = "3456"; 
    std::string b = "1234"; 
 
    std::string result = multiply(a, b);     
    std::cout << a << " * " << b << " = " << result <<std::endl; 
     
    return 0; 
}

为了方便我们先将各个乘数做了翻转处理，最后需要再将结果翻转回来。在运算过程中用来存放乘法运算结果的数组，我们没有进行移位处理同列相加，而是对角线相加，这样可以减少空间和运算步骤。上面的代码运行结果如下所示。

运行结果

因为字符串的长度没有特别的限制，所以上面的算法可以适用大整数运算。

分治算法

虽然上面的列竖式的方法可以很好的解决大整数乘法的问题，但是我们还用一种更加高效的方法可以选择，这就是分治(Divide and Conquer)算法。它是一种非常重要的算法，可以应用到很多领域，比如快速排序，二分搜索等。从算法的名字我们可以看出它是将大的问题拆分进行细化，由大变小，先将小的问题解决，最终将这个问题解决，所以叫Divide and Conquer。在这里我们可以通过这种方法将大整数进行拆分，拆分成一个个可以通过程序语言直接进行运算的小整进行计算，最后求得到大整数的值。

假设有两个大整数，我们设为a(大小为n位)和b(大小为m位)，这里我们将使用二分法对数据进行拆分，这两个整数我们可以分解为：

则,

令，

根据上面公式里，我们可以将a*b分解为四个小的整数的乘法，即z3,z2,z1,z0四个表达式。如果分解出来的乘法数值还是很大，还可以按照同样的方法进行拆解直到拆解成较小的数值乘法，直到计算机程序语言可以直接运算。

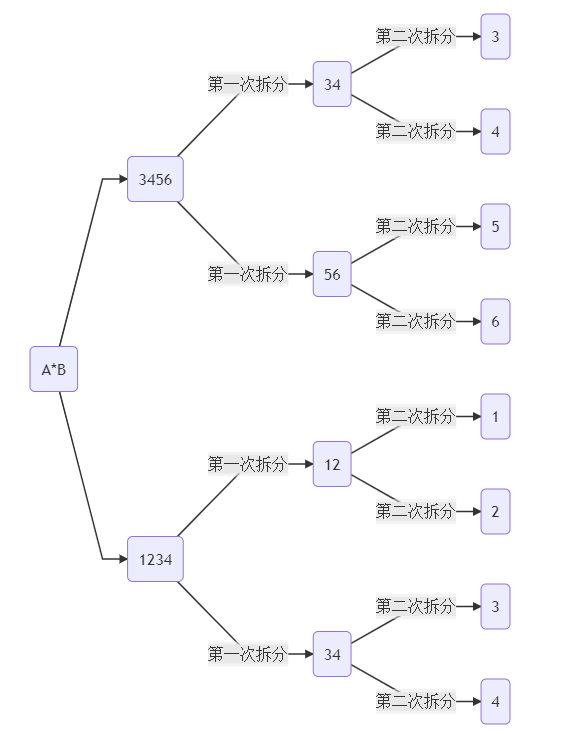
比如，上面的3456和1234相乘，参考下图通过二分法逐级对整数进行拆分，我们将两个整数拆分到一位整数进行运算。

3456和1234拆分步骤图

下面我们看一下分治算法的代码实现，这里我们使用递归的方法。

#include <iostream> 
#include <string> 
#include <stdlib.h> 
#include <vector> 
#include <cstring> 
#include <algorithm> 
#include <cmath> 
 
std::string add(std::string a, std::string b) 
{ 
    int N = std::max(a.size(), b.size()); 
    int sum[N]; 
    memset(sum, 0, sizeof(int)*N); 
     
    reverse(a.begin(),a.end()); 
    reverse(b.begin(),b.end()); 
 
    for(int i = 0; i< N; i++) 
    { 
        int bit_a = 0; 
        int bit_b = 0; 
        if(i < a.size()) bit_a = std::stoi(std::string(1, a.at(i))); 
        if(i < b.size()) bit_b = std::stoi(std::string(1, b.at(i))); 
 
        sum[i] += (bit_a + bit_b); 
 
        if(i < N-1 && sum[i]>9) 
        { 
            sum[i+1] = sum[i] / 10; 
            sum[i] %=10; 
        } 
    } 
 
    std::string result=""; 
    bool zeroStartFlag = true; 
    for (int i = N-1; i >= 0; i--) 
    { 
        if(sum[i]==0 && zeroStartFlag) 
        { 
            continue; 
        } 
         
        zeroStartFlag = false; 
        result.append(std::to_string(sum[i])); 
    } 
 
 
    return result; 
} 
 
std::string divideAndConquer(std::string a, std::string b) 
{ 
    if( a.size() < 2 && b.size() < 2)  
    { 
        return std::to_string(std::stoi(a) * std::stoi(b)); 
    } 
     
    int n = a.size(); 
    int m = b.size(); 
     
    int halfN = n/2; 
    int halfM = m/2; 
 
    std::string a0 = "0"; 
    std::string a1 = "0"; 
    if(a.size() > halfN && halfN > 0) 
    { 
        a1 = a.substr(0, halfN); 
        a0 = a.substr(halfN, a.size() - halfN); 
    } 
    else 
    { 
        a1 = "0"; 
        a0 = a; 
    } 
     
    std::string b0 = "0"; 
    std::string b1 = "0"; 
    if(b.size() > halfM && halfM > 0) 
    { 
        b1 = b.substr(0, halfM); 
        b0 = b.substr(halfM, b.size() - halfM); 
 
    } 
    else 
    { 
        b1 = "0"; 
        b0 = b; 
    } 
 
    std::string a1b1 = divideAndConquer(a1, b1); 
    std::string a0b0 = divideAndConquer(a0, b0); 
    std::string a1b0 = divideAndConquer(a1, b0); 
    std::string a0b1 = divideAndConquer(a0, b1); 
     
    a1b1.append((n - halfN) + (m - halfM), '0'); 
    a1b0.append(n - halfN, '0'); 
    a0b1.append(m - halfM, '0'); 
 
    std::string result = ""; 
    result = add(a1b1, a1b0); 
    result = add(result, a0b1); 
    result = add(result, a0b0); 
 
    return result; 
} 
 
int main() 
{ 
    std::string a = "3456"; 
    std::string b = "1234"; 
 
    std::cout << a << " * " << b << " = " << divideAndConquer(a, b) << std::endl;  
 
    return 0; 
}

程序的运行结果如下：

分治算法运行结果

本文转载自微信公众号「Will的大食堂」，可以通过以下二维码关注。转载本文请联系Will的大食堂公众号。